Граф Фолькмана - Folkman graph
| Граф Фолькмана | |
|---|---|
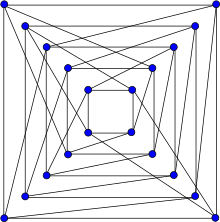 Граф Фолкмана | |
| Названный в честь | Джон Фолкман |
| Вершины | 20 |
| Края | 40 |
| Радиус | 3 |
| Диаметр | 4 |
| Обхват | 4 |
| Автоморфизмы | 3840 |
| Хроматическое число | 2 |
| Хроматический индекс | 4 |
| Толщина книги | 3 |
| Номер очереди | 2 |
| Характеристики | Гамильтониан Обычный Двудольный Полусимметричный Эйлеров Идеально |
| Таблица графиков и параметров | |
в математический поле теория графов, то Граф Фолькмана, названный в честь Джон Фолкман, это двудольный 4-обычный график с 20 вершины и 40 граней.[1]
Граф Фолкмана Гамильтониан и имеет хроматическое число 2, хроматический индекс 4, радиус 3, диаметр 4 и обхват 4. Это также 4-вершинно-связанный и 4-реберный идеальный график. Она имеет толщина книги 3 и номер очереди 2.[2]
Алгебраические свойства
В группа автоморфизмов графа Фолкмана транзитивно действует на его ребрах, но не на его вершинах. Это наименьший неориентированный граф, который реберно-транзитивный и обычный, но не вершинно-транзитивный.[3] Такие графы называются полусимметричные графы и впервые были изучены Фолкманом в 1967 году, который открыл граф на 20 вершинах, который теперь носит его имя.[4]
Как полусимметричный граф, граф Фолкмана имеет вид двудольный, и его группа автоморфизмов действует транзитивно на каждом из двух множеств вершин двудольности. На диаграмме ниже, указывающей хроматическое число графа, зеленые вершины не могут быть отображены на красные никаким автоморфизмом, но любая красная вершина может быть отображена на любую другую красную вершину, а любая зеленая вершина может быть отображена на любую другую зеленую вершину. .
В характеристический многочлен графа Фолкмана есть .
Галерея

В хроматический индекс графа Фолкмана равно 4.

В хроматическое число графа Фолкмана равно 2.

Граф Фолкмана Гамильтониан.
Рекомендации
- ^ Вайсштейн, Эрик В. «Граф Фолькмана». MathWorld.
- ^ Вольц, Джессика; Инженерные линейные схемы с SAT. Магистерская работа, Тюбингенский университет, 2018 г.
- ^ Скиена, С. Реализация дискретной математики: комбинаторика и теория графов с помощью Mathematica. Ридинг, Массачусетс: Эддисон-Уэсли, стр. 186-187, 1990.
- ^ Фолькман, Дж. (1967), "Правильные линейно-симметричные графы", Журнал комбинаторной теории, 3 (3): 215–232, Дои:10.1016 / S0021-9800 (67) 80069-3




