Гигантское магнитосопротивление - Giant magnetoresistance
Гигантское магнитосопротивление (GMR) это квантово-механический магнитосопротивление эффект наблюдается в многослойность состоит из чередующихся ферромагнитный и немагнитные проводящие слои. 2007 год Нобелевская премия по физике был присужден Альберт Ферт и Петер Грюнберг за открытие GMR.
Эффект проявляется в значительном изменении электрическое сопротивление в зависимости от того, намагничивание смежных ферромагнитный слои расположены параллельно или антипараллельный выравнивание. Общее сопротивление относительно низкое для параллельного совмещения и относительно высокое для антипараллельного совмещения. Направлением намагничивания можно управлять, например, путем приложения внешнего магнитного поля. Эффект основан на зависимости рассеяния электронов от ориентации спина.
Основное применение GMR - датчики магнитного поля, которые используются для чтения данных в жесткие диски, биосенсоры, микроэлектромеханические системы (MEMS) и другие устройства.[1] Многослойные структуры GMR также используются в магниторезистивная память с произвольным доступом (MRAM) как ячейки, в которых хранится один бит информации.
В литературе термин гигантское магнитосопротивление иногда путают с колоссальное магнитосопротивление ферромагнитных и антиферромагнитных полупроводников, не имеющего отношения к многослойной структуре.[2][3]

Формулировка
Магнитосопротивление - это зависимость электрическое сопротивление образца от напряженности внешнего магнитного поля. Численно он характеризуется величиной
где R (H) - сопротивление образца в магнитном поле H, а R (0) соответствует H = 0.[4] Альтернативные формы этого выражения могут использовать удельное электрическое сопротивление вместо сопротивления, другой знак для δЧАС,[5] и иногда нормируются на R (H), а не на R (0).[6]
Термин «гигантское магнитосопротивление» указывает на то, что величина δЧАС для многослойных структур значительно превышает анизотропное магнитосопротивление, которое имеет типичное значение в пределах нескольких процентов.[7][8]
История
GMR был открыт в 1988 году независимо[9][10] группами Альберт Ферт из Университет Париж-Юг, Франция и Петер Грюнберг из Forschungszentrum Jülich, Германия. Практическое значение этого экспериментального открытия было признано Нобелевской премией по физике, присужденной Ферту и Грюнбергу в 2007 году.[11]
Первые шаги
Первая математическая модель, описывающая влияние намагниченности на подвижность носителей заряда в твердых телах, связанных со спином этих носителей, было сообщено в 1936 году. Экспериментальные доказательства потенциального увеличения δЧАС известен с 1960-х годов. К концу 1980-х анизотропное магнитосопротивление было хорошо изучено.[12][13] но соответствующее значение δЧАС не превышала нескольких процентов.[7] Увеличение δЧАС стало возможным с появлением таких методов пробоподготовки, как молекулярно-лучевая эпитаксия, что позволяет изготавливать многослойные тонкие пленки толщиной в несколько нанометров.[14]
Эксперимент и его интерпретация
Ферт и Грюнберг изучали электрическое сопротивление структур, состоящих из ферромагнитных и неферромагнитных материалов. В частности, Ферт работал над многослойными пленками, а Грюнберг в 1986 году открыл антиферромагнитное обменное взаимодействие в пленках Fe / Cr.[14]
Обнаружение GMR было выполнено двумя группами на немного разных образцах. Группа Ферта использовала сверхрешетки (001) Fe / (001) Cr, в которых слои Fe и Cr были нанесены в высоком вакууме на подложку (001) GaAs, поддерживаемую при 20 ° C, а измерения магнитосопротивления проводились при низкой температуре (обычно 4,2 К).[10] Работа Грюнберга была проведена на мультислоях Fe и Cr на (110) GaAs при комнатной температуре.[9]
В мультислоях Fe / Cr со слоями железа толщиной 3 нм увеличение толщины немагнитных слоев Cr с 0,9 до 3 нм ослабляло антиферромагнитную связь между слоями Fe и уменьшало поле размагничивания, которое также уменьшалось, когда образец был нагревается от 4,2 К до комнатной температуры. Изменение толщины немагнитных слоев привело к значительному снижению остаточной намагниченности в петле гистерезиса. Электрическое сопротивление изменилось до 50% с внешним магнитным полем при 4,2 К. Ферт назвал новый эффект гигантским магнитосопротивлением, чтобы подчеркнуть его отличие от анизотропного магнитосопротивления.[10][15] Эксперимент Грюнберга[9] сделал то же открытие, но эффект был менее выраженным (3% по сравнению с 50%) из-за того, что образцы находились при комнатной температуре, а не при низкой температуре.
Первооткрыватели предположили, что в основе эффекта лежит спин-зависимое рассеяние электронов в сверхрешетке, в частности, зависимость сопротивления слоев от относительной ориентации намагниченности и электронных спинов.[9][10] Теория ГМС для разных направлений течения была разработана в последующие годы. В 1989 г. Камли и Барнась рассчитали геометрию «тока в плоскости» (CIP), при которой ток течет вдоль слоев в классическом приближении:[16] тогда как Леви и другие. использовал квантовый формализм.[17] Теория GMR для тока, перпендикулярного слоям (ток, перпендикулярный плоскости или геометрия CPP), известная как теория Вале-Ферта, была представлена в 1993 году.[18] Приложения отдают предпочтение геометрии CPP[19] поскольку он обеспечивает большее магнитосопротивление (δЧАС),[20] что приводит к большей чувствительности устройства.[21]
Теория
Основы
Спин-зависимое рассеяние

В магнитоупорядоченных материалах решающее влияние на электрическое сопротивление оказывает рассеяние электронов на магнитной подрешетке кристалла, которая образована кристаллографически эквивалентными атомами с ненулевым магнитным моментом. Рассеяние зависит от относительной ориентации электронных спинов и этих магнитных моментов: самое слабое, когда они параллельны, и самое сильное, когда они антипараллельны; он относительно силен в парамагнитном состоянии, в котором магнитные моменты атомов имеют случайную ориентацию.[7][22]
Для хороших проводников, таких как золото или медь, Уровень Ферми лежит в пределах зр группа, и d полоса полностью заполнена. В ферромагнетиках зависимость рассеяния электронов на атомах от ориентации их магнитных моментов связана с заполнением полосы, отвечающей за магнитные свойства металла, например 3d лента для железа, никеля или кобальта. В d полоса ферромагнетиков расщепляется, так как содержит разное количество электронов со спинами, направленными вверх и вниз. Следовательно, плотность электронных состояний на уровне Ферми также различна для спинов, направленных в противоположные стороны. Уровень Ферми для электронов с мажоритарным спином находится в пределах зр полосы, и их транспорт аналогичен в ферромагнетиках и немагнитных металлах. Для электронов с неосновным спином зр и d полосы гибридизованы, а уровень Ферми находится в пределах d группа. Гибридные скорость полоса имеет высокую плотность состояний, что приводит к более сильному рассеянию и, следовательно, к более короткой длина свободного пробега λ для неосновного спина, чем для электронов со спином большинства. В никеле, легированном кобальтом, отношение λ↑/ λ↓ может достигать 20.[23]
Согласно Теория Друде, проводимость пропорциональна λ, которая в тонких металлических пленках составляет от нескольких до нескольких десятков нанометров. Электроны «запоминают» направление спина в пределах так называемой длины спиновой релаксации (или длины спиновой диффузии), которая может значительно превышать длину свободного пробега. Спин-зависимый перенос относится к зависимости электропроводности от направления спина носителей заряда. В ферромагнетиках это происходит за счет переходов электронов между нерасщепленными 4s и разделить 3d группы.[7]
В некоторых материалах взаимодействие между электронами и атомами является самым слабым, когда их магнитные моменты антипараллельны, а не параллельны. Комбинация обоих типов материалов может привести к так называемому обратному эффекту GMR.[7][24]
- Ленточная структура (слева) и плотность состояний (верно)

Медь (немагнитный металл). F - уровень Ферми. По вертикальной оси отложена энергия в эВ.

Кобальт (большинство спинов)
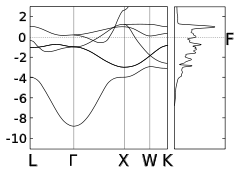
Кобальт (миноритарные спины)
Геометрия CIP и CPP

Электрический ток может проходить через магнитные сверхрешетки двумя способами. В геометрии тока в плоскости (CIP) ток течет по слоям, а электроды расположены на одной стороне структуры. В конфигурации тока перпендикулярно плоскости (CPP) ток проходит перпендикулярно слоям, а электроды расположены по разные стороны сверхрешетки.[7] Геометрия CPP приводит к более чем двукратному увеличению GMR, но ее труднее реализовать на практике, чем конфигурацию CIP.[25][26]
Транспорт носителей через магнитную сверхрешетку
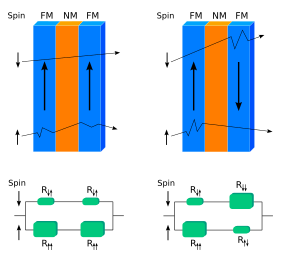
Магнитное упорядочение различается в сверхрешетках с ферромагнитным и антиферромагнитным взаимодействием между слоями. В первом случае направления намагничивания одинаковы в разных ферромагнитных слоях в отсутствие приложенного магнитного поля, тогда как во втором случае противоположные направления в мультислое чередуются. Электроны, проходящие через ферромагнитную сверхрешетку, взаимодействуют с ней намного слабее, когда их спиновые направления противоположны намагниченности решетки, чем когда они параллельны ей. Для антиферромагнитной сверхрешетки такая анизотропия не наблюдается; в результате он рассеивает электроны сильнее, чем ферромагнитная сверхрешетка, и демонстрирует более высокое электрическое сопротивление.[7]
Применение эффекта GMR требует динамического переключения между параллельной и антипараллельной намагниченностью слоев в сверхрешетке. В первом приближении плотность энергии взаимодействия двух ферромагнитных слоев, разделенных немагнитным слоем, пропорциональна скалярному произведению их намагниченностей:
Коэффициент J является колебательной функцией толщины немагнитного слоя ds; следовательно J может менять свою величину и знак. Если ds значение соответствует антипараллельному состоянию, тогда внешнее поле может переключить сверхрешетку из антипараллельного состояния (высокое сопротивление) в параллельное состояние (низкое сопротивление). Общее сопротивление конструкции можно записать как
где R0 - сопротивление ферромагнитной сверхрешетки, ΔR - приращение ГМС, θ - угол между намагниченностями соседних слоев.[25]
Математическое описание
Явление GMR можно описать с помощью двух каналов спиновой проводимости, соответствующих проводимости электронов, для которых сопротивление является минимальным или максимальным. Связь между ними часто определяют через коэффициент спиновой анизотропии β. Этот коэффициент можно определить с помощью минимума и максимума удельного электрического сопротивления ρF ± для спин-поляризованного тока в виде
куда ρF - среднее сопротивление ферромагнетика.[27]
Модель резистора для конструкций CIP и CPP
Если рассеяние носителей заряда на границе раздела между ферромагнитным и немагнитным металлом невелико, а направление электронных спинов сохраняется достаточно долго, удобно рассматривать модель, в которой полное сопротивление образца представляет собой комбинацию сопротивления магнитного и немагнитного слоев.
В этой модели существует два канала проводимости для электронов с различными направлениями спина относительно намагниченности слоев. Следовательно, эквивалентная схема структуры GMR состоит из двух параллельных соединений, соответствующих каждому из каналов. В этом случае GMR можно выразить как
Здесь индексом R обозначена коллинеарная и противоположно ориентированная намагниченность в слоях, х = Ь / а - отношение толщин магнитного и немагнитного слоев, а ρN - удельное сопротивление немагнитного металла. Это выражение применимо как для структур CIP, так и для CPP. При условии это соотношение можно упростить, используя коэффициент асимметрии спина
Такое устройство, сопротивление которого зависит от ориентации электронного спина, называется спиновой клапан. Он «открытый», если намагниченности его слоев параллельны, и «закрытый» в противном случае.[28]
Модель Valet-Fert
В 1993 году Тьерри Вале и Альберт Фер представили модель гигантского магнитосопротивления в геометрии CPP, основанную на уравнениях Больцмана. В этой модели химический потенциал внутри магнитного слоя разделен на две функции, соответствующие электронам со спинами, параллельными и антипараллельными намагниченности слоя. Если немагнитный слой достаточно тонкий, то во внешнем поле E0 поправки к электрохимическому потенциалу и полю внутри образца примут вид
куда ℓs - средняя длина спиновой релаксации, а координата z отсчитывается от границы между магнитным и немагнитным слоями (z <0 соответствует ферромагнетику).[18] Таким образом, электроны с большим химическим потенциалом будут накапливаться на границе ферромагнетика.[29] Это можно представить как потенциал накопления спинов. VВ КАЧЕСТВЕ или так называемым межфазным сопротивлением (присущим границе между ферромагнетиком и немагнитным материалом)
куда j - плотность тока в образце, ℓsN и ℓSF - длина спиновой релаксации в немагнитных и магнитных материалах соответственно.[30]
Подготовка устройства
Материалы и экспериментальные данные.
Многие комбинации материалов демонстрируют GMR,[31] и наиболее распространены следующие:
- FeCr[10]
- Co10Cu90: δЧАС = 40% при комнатной температуре[32]
- [110] Co95Fe5/ Cu: δЧАС = 110% при комнатной температуре.[31]
Магнитосопротивление зависит от многих параметров, таких как геометрия устройства (CIP или CPP), его температура и толщина ферромагнитных и немагнитных слоев. При температуре 4,2 К и толщине слоев кобальта 1,5 нм увеличение толщины слоев меди dCu от 1 до 10 нм уменьшилось δЧАС от 80 до 10% в геометрии CIP. Между тем, в геометрии CPP максимум δЧАС (125%) наблюдалась для dCu = 2,5 нм, и увеличивая dCu до 10 нм уменьшено δЧАС до 60% колебательным образом.[33]
При нагревании сверхрешетки Co (1,2 нм) / Cu (1,1 нм) от почти нуля до 300 K ее δЧАС уменьшился с 40 до 20% в геометрии CIP и со 100 до 55% в геометрии CPP.[34]
Немагнитные слои могут быть неметаллическими. Например, δЧАС до 40% было продемонстрировано для органических слоев при 11 К.[35] Графеновые спиновые клапаны различной конструкции продемонстрировали δЧАС около 12% при 7 К и 10% при 300 К, что намного ниже теоретического предела 109%.[36]
Эффект GMR можно усилить с помощью спиновых фильтров, отбирающих электроны с определенной ориентацией спина; они сделаны из металлов, таких как кобальт. Для фильтра толщины т изменение проводимости ΔG можно выразить как
где ΔGSV - изменение проводимости спинового клапана без фильтра, ΔGж - максимальное увеличение проводимости с фильтром, а β - параметр фильтрующего материала.[37]
Виды GMR
GMR часто классифицируют по типу устройств, которые проявляют эффект.[38]
Фильмы
Антиферромагнитные сверхрешетки
ГМС в пленках впервые наблюдали Ферт и Грюнберг при исследовании сверхрешеток, состоящих из ферромагнитных и немагнитных слоев. Толщина немагнитных слоев была выбрана такой, чтобы взаимодействие между слоями было антиферромагнитным, а намагниченность в соседних магнитных слоях была антипараллельной. Тогда внешнее магнитное поле могло бы сделать векторы намагниченности параллельными, тем самым влияя на электрическое сопротивление конструкции.[10]
Магнитные слои в таких структурах взаимодействуют посредством антиферромагнитной связи, что приводит к колебательной зависимости GMR от толщины немагнитного слоя. В первых датчиках магнитного поля на антиферромагнитных сверхрешетках поле насыщения было очень большим, до десятков тысяч Эрстед, из-за сильного антиферромагнитного взаимодействия между их слоями (сделанными из хрома, железа или кобальта) и сильными полями анизотропии в них. Поэтому чувствительность устройств была очень низкой. Использование пермаллой для магнитного и серебра для немагнитных слоев снизили поле насыщения до десятков эрстед.[39]
Спиновые клапаны с использованием обменного смещения
В наиболее удачных спиновых клапанах эффект GMR возникает из-за обменного смещения. Они состоят из чувствительного слоя, «фиксированного» слоя и антиферромагнитного слоя. Последний слой фиксирует направление намагниченности в «фиксированном» слое. Чувствительный и антиферромагнитный слои сделаны тонкими, чтобы уменьшить сопротивление конструкции. Клапан реагирует на внешнее магнитное поле изменением направления намагниченности в чувствительном слое относительно «неподвижного» слоя.[39]
Основным отличием этих спиновых клапанов от других многослойных устройств ГМС является монотонная зависимость амплитуды воздействия от толщины. dN немагнитных слоев:
где δH0 - нормировочная постоянная, λN - длина свободного пробега электронов в немагнитном материале, d0 эффективная толщина, которая включает взаимодействие между слоями.[38][40] Зависимость от толщины ферромагнитного слоя может быть представлена как:
Параметры имеют то же значение, что и в предыдущем уравнении, но теперь они относятся к ферромагнитному слою.[31]
Невзаимодействующие многослойные (псевдоспиновые клапаны)
ГМС можно наблюдать и в отсутствие слоев антиферромагнитной связи. В этом случае магнитосопротивление возникает из-за разницы в коэрцитивных силах (например, для пермаллоя оно меньше, чем для кобальта). В мультислоях, таких как пермаллой / Cu / Co / Cu, внешнее магнитное поле переключает направление намагниченности насыщения на параллельное в сильных полях и на антипараллельное в слабых полях. Такие системы обладают меньшим полем насыщения и большей величиной δЧАС чем сверхрешетки с антиферромагнитной связью.[39] Аналогичный эффект наблюдается в структурах Co / Cu. Существование этих структур означает, что GMR не требует межслойной связи и может происходить из распределения магнитных моментов, которым можно управлять с помощью внешнего поля.[41]
Обратный эффект GMR
В обратном ГМС сопротивление минимально при антипараллельной ориентации намагниченности в слоях. Обратный ГМС наблюдается, когда магнитные слои состоят из разных материалов, таких как NiCr / Cu / Co / Cu. Сопротивление для электронов с противоположными спинами можно записать как ; он имеет разные значения, то есть разные коэффициенты β для электронов со спином вверх и вниз. Если слой NiCr не слишком тонкий, его вклад может превышать вклад слоя Co, что приводит к обратному GMR.[24] Отметим, что инверсия GMR зависит от знака товар коэффициентов β в соседних ферромагнитных слоях, но не от знаков отдельных коэффициентов.[34]
Обратный ГМС также наблюдается, если сплав NiCr заменяется никелем, легированным ванадием, но не при легировании никеля железом, кобальтом, марганцем, золотом или медью.[42]
GMR в зернистых структурах
ГМС в гранулированных сплавах ферромагнитных и немагнитных металлов был открыт в 1992 г. и впоследствии объяснен спин-зависимым рассеянием носителей заряда на поверхности и в объеме зерен. Зерна образуют ферромагнитные кластеры диаметром около 10 нм, встроенные в немагнитный металл, образуя своего рода сверхрешетку. Необходимым условием ГМС в таких структурах является плохая взаимная растворимость его компонентов (например, кобальта и меди). Их свойства сильно зависят от температуры измерения и отжига. Они также могут демонстрировать обратный GMR.[32][43]
Приложения
Датчики спин-клапана
Основной принцип

Одно из основных применений материалов GMR - датчики магнитного поля, например, в жестких дисках.[25] и биосенсоры,[31] а также детекторы колебаний в MEMS.[31] Типичный датчик на основе GMR состоит из семи слоев:
- Силиконовая подложка,
- Связующий слой,
- Чувствительный (нефиксированный) слой,
- Немагнитный слой,
- Фиксированный слой,
- Антиферромагнитный (пиннинг) слой,
- Защитный слой.
Связующий и защитный слои часто состоят из тантал, а типичным немагнитным материалом является медь. В чувствительном слое намагниченность может быть переориентирована внешним магнитным полем; он обычно изготавливается из сплавов NiFe или кобальта. FeMn или NiMn можно использовать в качестве антиферромагнитного слоя. Неподвижный слой изготовлен из магнитного материала, например кобальта. Такой датчик имеет асимметричную петлю гистерезиса из-за наличия магнитотвердого фиксированного слоя.[44][45]
Спиновые клапаны могут проявлять анизотропное магнитосопротивление, что приводит к асимметрии кривой чувствительности.[46]
Жесткие диски
В жесткие диски (HDD) информация кодируется с помощью магнитные домены, а изменение направления их намагничивания связано с логическим уровнем 1, в то время как отсутствие изменений представляет собой логический 0. Существует два метода записи: продольный и перпендикулярный.
В продольном методе намагниченность перпендикулярна поверхности. Между доменами образуется переходная область (доменные стенки), в которой магнитное поле выходит из материала. Если доменная стенка расположена на границе двух доменов северного полюса, то поле направлено наружу, а для двух доменов южного полюса - внутрь. Чтобы считывать направление магнитного поля над доменной стенкой, направление намагничивания фиксируется нормально к поверхности в антиферромагнитном слое и параллельно поверхности в чувствительном слое. Изменение направления внешнего магнитного поля отклоняет намагниченность в чувствительном слое. Когда поле стремится выровнять намагниченности в чувствительном и фиксированном слоях, электрическое сопротивление датчика уменьшается, и наоборот.[47]
Магнитная RAM

Ячейка магниторезистивная память с произвольным доступом (MRAM) имеет структуру, аналогичную датчику спин-клапана. Значение сохраненных битов может быть закодировано через направление намагничивания в слое датчика; это считывается путем измерения сопротивления конструкции. Преимуществами этой технологии являются независимость от источника питания (информация сохраняется при отключении питания из-за потенциального барьера для переориентации намагниченности), низкое энергопотребление и высокая скорость.[25]
В типичном запоминающем устройстве на основе GMR структура CIP расположена между двумя проводами, ориентированными перпендикулярно друг другу. Эти проводники называются линиями строк и столбцов. Импульсы электрического тока, проходящие через линии, создают вихревое магнитное поле, которое влияет на структуру ГМС. Силовые линии имеют форму эллипсоида, а направление поля (по или против часовой стрелки) определяется направлением тока в линии. В структуре ГМС намагниченность ориентирована вдоль линии.
Направление поля, создаваемого линией колонны, почти параллельно магнитным моментам, и оно не может их переориентировать. Линия ряда перпендикулярна и независимо от величины поля может повернуть намагниченность всего на 90 °. При одновременном прохождении импульсов по строкам и столбцам полное магнитное поле в месте расположения ГМС-структуры будет направлено под острым углом к одной точке и тупым углом к другим. Если значение поля превышает какое-то критическое значение, последнее меняет свое направление.
Для описываемой ячейки существует несколько способов хранения и чтения. В одном методе информация хранится в чувствительном слое; он считывается при измерении сопротивления и стирается при считывании. В другой схеме информация хранится в фиксированном слое, для чего требуются более высокие токи записи по сравнению с токами чтения.[48]
Туннельное магнитосопротивление (TMR) - это расширение спинового клапана GMR, в котором электроны перемещаются со своими спинами, ориентированными перпендикулярно слоям, через тонкий изолирующий туннельный барьер (заменяющий неферромагнитную прокладку). Это позволяет добиться большего импеданса, большего магнитосопротивление значение (~ 10x при комнатной температуре) и незначительная температурная зависимость. TMR теперь заменил GMR в MRAM и Дисковый привод, в частности, для высокой плотности и перпендикулярной записи.[49]
Другие приложения
Магниторезистивные изоляторы для бесконтактной передачи сигналов между двумя электрически изолированными частями электрических цепей были впервые продемонстрированы в 1997 году в качестве альтернативы. оптоизоляторы. А Мост Уитстона четырех идентичных устройств GMR нечувствителен к однородному магнитному полю и реагирует только тогда, когда направления поля антипараллельны в соседних плечах моста. Такие устройства появились в 2003 году и могут использоваться как выпрямители с линейной частотной характеристикой.[31]
Примечания
- ^ Эта схема не включает гистерезис, поскольку форма ее петли в сверхрешетках сильно зависит от толщины немагнитного слоя d. Ферт наблюдал четкий гистерезис с полем насыщения ~ 4 кГс и остаточной намагниченностью 60% от значения насыщения при dCu= 1,8 нм. Когда дCu уменьшился до 0,9 нм, ГМС достиг максимума, но петля гистерезиса схлопнулась; поле насыщения увеличилось до 20 кГс, но остаточное поле было очень маленьким (Байбич и др. 1988 г. )
Цитаты
- ^ Рейг, Кардосо и Мукхопадхьяй, 2013 г..
- ^ Нагаев, Э. Л. (1996). «Манганиты лантана и другие магнитопроводы с гигантским магнитосопротивлением». Успехи СССР. (на русском). 166 (8): 833–858. Дои:10.3367 / УФН.0166.199608б.0833.
- ^ Raveau, B .; Рао, С. Н. Р., ред. (1998). Колоссальное магнитосопротивление, порядок заряда и связанные свойства оксидов марганца. World Scientific Publishing Co. с. 2. ISBN 978-981-02-3276-4.
- ^ Hirota, E .; Иномата, К. (2002a). Гигантские устройства магниторезистивного действия. Springer. п. 30. ISBN 978-3-540-41819-1.
- ^ Никитин, С. А. (2004). "Гигантское магнитосопротивление" (PDF). Соросовский обозревательный журнал. 8 (2): 92–98.[постоянная мертвая ссылка ]
- ^ Пиппард, Альфред Брайан (2009). Магнитосопротивление в металлах. Кембриджские исследования по физике низких температур. Том 2. Издательство Кембриджского университета. п. 8. ISBN 978-052111880-4.
- ^ а б c d е ж грамм Чапперт, Клод; Ферт, Альберт; Нгуен Ван Дау, Фредерик (2007). «Появление спиновой электроники в хранении данных». Материалы Природы. 6 (11): 813–823. Bibcode:2007НатМа ... 6..813C. Дои:10.1038 / nmat2024. PMID 17972936.
- ^ Hirota, E .; Иномата, К. (2002b). Гигантские устройства магниторезистивного действия. Springer. п. 23. ISBN 978-3-540-41819-1.
- ^ а б c d Бинаш, Г .; Грюнберг; Зауренбах; Зинн (1989). «Повышенное магнитосопротивление в слоистых магнитных структурах с антиферромагнитным межслоевым обменом». Физический обзор B. 39 (7): 4828–4830. Bibcode:1989ПхРвБ..39.4828Б. Дои:10.1103 / PhysRevB.39.4828. PMID 9948867.
- ^ а б c d е ж Байбич и др. 1988 г..
- ^ «Нобелевская премия по физике 2007 г.». Нобелевский фонд. Архивировано из оригинал 5 августа 2011 г.. Получено 27 февраля 2011.
- ^ Зейтц, Фредерик; Тернбулл, Дэвид (1957). Достижения в исследованиях и приложениях. Физика твердого тела. Том 5. Академическая пресса. п. 31. ISBN 978-012607705-6.
- ^ Абоаф, Дж. А. (9 октября 1984 г.). «Новые магниторезистивные материалы». Патент США 4476454. Получено 11 апреля 2011.
- ^ а б Ферт, А. (2008a). «Нобелевская лекция: происхождение, развитие и будущее спинтроники *». Ред. Мод. Phys. 80 (4): 1517–1530. Bibcode:2008RvMP ... 80.1517F. Дои:10.1103 / RevModPhys.80.1517. Ферт, А. (2008b). «Зарождение, развитие и будущее спинтроники». Успехи СССР.. 178 (12): 1336–1348. Дои:10.3367 / УФН.0178.200812ф.1336. (Отпечатки Нобелевская лекция 2007 г. от 8 декабря 2007 г.
- ^ Цымбал и Петтифор 2001, п. 120.
- ^ Camley, R.E .; Барнась, Дж. (1989). «Теория эффектов гигантского магнитосопротивления в магнитных слоистых структурах с антиферромагнитной связью». Phys. Rev. Lett. 63 (6): 664–667. Bibcode:1989PhRvL..63..664C. Дои:10.1103 / PhysRevLett.63.664. PMID 10041140.
- ^ Ферт, Альберт; Леви, Питер М .; Чжан, Шуфэн (1990). «Электропроводность магнитных многослойных структур». Phys. Rev. Lett. 65 (13): 1643–1646. Bibcode:1990ПхРвЛ..65.1643Л. Дои:10.1103 / PhysRevLett.65.1643. PMID 10042322.
- ^ а б Valet, Т .; Ферт, А. (1993). «Теория перпендикулярного магнитосопротивления в магнитных мультислоях». Физический обзор B. 48 (10): 7099–7113. Bibcode:1993ПхРвБ..48.7099В. Дои:10.1103 / PhysRevB.48.7099. PMID 10006879.
- ^ Нагасака, К. (30 июня 2005 г.). «Технология CPP-GMR для будущей магнитной записи высокой плотности» (PDF). Fujitsu. Архивировано из оригинал (PDF) 6 августа 2008 г.. Получено 11 апреля 2011.
- ^ Синдзё 2009.
- ^ Бушоу 2005, п. 580.
- ^ Цымбал и Петтифор 2001, п. 122.
- ^ Цымбал и Петтифор 2001 С. 126–132.
- ^ а б Бушоу 2005, п. 254.
- ^ а б c d Хвалковский, А .. В. "Гигантское магнитосопротивление: от открытия до Нобелевской программы". AMT & C. Архивировано из оригинал 8 января 2015 г.. Получено 27 февраля 2011.
- ^ Bass, J .; Пратт, В. П. (1999b). «Токоперпендикулярное (CPP) магнитосопротивление в магнитных металлических многослойных слоях». Журнал магнетизма и магнитных материалов. 200 (1–3): 274–289. Bibcode:1999JMMM..200..274B. Дои:10.1016 / S0304-8853 (99) 00316-9.
- ^ Третьяк, Львов и Барабанов 2002, п. 243.
- ^ Третьяк, Львов и Барабанов 2002, стр. 258–261, 247–248.
- ^ Stöhr, J .; Зигманн, Х.С. (2006a). Магнетизм: от основ до наномасштабной динамики. Springer-Verlag Berlin Heidelberg. п. 641. ISBN 978-354030282-7.
- ^ Stöhr, J .; Зигманн, Х.С. (2006b). Магнетизм: от основ до наномасштабной динамики. Springer-Verlag Berlin Heidelberg. С. 648–649. ISBN 978-354030282-7.
- ^ а б c d е ж Коухорн, Р. (2003). «Новые магнитоэлектронные материалы и устройства» (PDF). Гигантское магнитосопротивление и магнитные взаимодействия в спиновых клапанах с обменным смещением. Конспект лекций. Technische Universiteit Eindhoven. Архивировано из оригинал (PDF) 24 июля 2011 г.. Получено 25 апреля 2011.
- ^ а б Грановский, А.Б .; Илин, М .; Жуков, А .; Жукова, В .; Гонсалес, Дж. (2011). «Гигантское магнитосопротивление гранулированных микропроводов: спин-зависимое рассеяние в интегральных прокладках» (PDF). Физика твердого тела. 53 (2): 320–322. Bibcode:2011ФСС ... 53..320Г. Дои:10.1134 / S1063783411020107. S2CID 119767942.
- ^ Бушоу 2005, п. 248.
- ^ а б Bass, J .; Пратт, У. П. (1999a). «Токоперпендикулярное (CPP) магнитосопротивление в магнитных металлических многослойных слоях». Журнал магнетизма и магнитных материалов. 200 (1–3): 274–289. Bibcode:1999JMMM..200..274B. Дои:10.1016 / S0304-8853 (99) 00316-9.
- ^ Солнце, Дали; Инь, L; Вс, ц; Guo, H; Gai, Z; Zhang, X. G .; Ward, T. Z .; Cheng, Z; Шен, Дж. (2010). «Гигантское магнитосопротивление в органических спиновых клапанах». Письма с физическими проверками. 104 (23): 236602. Bibcode:2010PhRvL.104w6602S. Дои:10.1103 / PhysRevLett.104.236602. PMID 20867259.
- ^ Цинь, Руи; Лу, Цзин; Лай, Линь; Чжоу, Цзин; Ли, Хун; Лю, Цихан; Ло, Гуанфу; Чжао, Лина; Гао, Чжэнсян; Мэй, Вай Нин; Ли, Гуанпин (2010). «Гигантское магнитосопротивление при комнатной температуре более одного миллиарда процентов в устройстве с голой графеновой нанолентой». Phys. Ред. B. 81 (23): 233403. Bibcode:2010PhRvB..81w3403Q. Дои:10.1103 / PhysRevB.81.233403.
- ^ Bland, J. A. C .; Генрих Б., ред. (2005). Ультратонкие магнитные структуры. Применение наномагнетизма. IV. Springer. С. 161–163. ISBN 978-3-540-21954-5.
- ^ а б Цымбал, Евгений. «Структуры GMR». Университет Небраски-Линкольн. Архивировано из оригинал 12 декабря 2012 г.. Получено 11 апреля 2011.
- ^ а б c Налва, Хари Сингх (2002a). Справочник тонкопленочных материалов: наноматериалы и магнитные тонкие пленки. Том 5. Академическая пресса. С. 518–519. ISBN 978-012512908-4.
- ^ Налва, Хари Сингх (2002b). Справочник тонкопленочных материалов: наноматериалы и магнитные тонкие пленки. Том 5. Академическая пресса. С. 519, 525–526. ISBN 978-012512908-4.
- ^ Пу, Ф. С. (1996). Shang, C.H .; Ван, Ю. Дж. (Ред.). Аспекты современного магнетизма: конспекты лекций восьмой Китайской международной летней школы физики Пекин, Китай, 28 августа - 7 сентября 1995 г.. World Scientific. п. 122. ISBN 978-981022601-5.
- ^ Гимарайнш, Альберто П. (2009). Принципы наномагнетизма. Springer. п. 132. ISBN 978-3-642-01481-9.
- ^ «Магнитные домены в зернистых материалах ГМС». Национальный институт стандартов и технологий. Архивировано из оригинал 12 августа 2011 г.. Получено 12 марта 2011.
- ^ Вормингтон, Мэтью; Браун, Эллиот (2001). Исследование спин-клапанных структур с гигантским магнитосопротивлением (ГМС) с использованием рентгеновской дифракции и отражательной способности (PDF). Достижения в рентгеновском анализе - материалы Денверских рентгеновских конференций. Том 44. Международный центр дифракционных данных. С. 290–294. Архивировано из оригинал (PDF) 5 сентября 2014 г.
- ^ Dodrill, B.C .; Келли, Б. Дж. «Магнитная поточная метрология для датчиков с вращающимся клапаном GMR» (PDF). Криотроника Lake Shore. Архивировано из оригинал (PDF) 5 января 2011 г.. Получено 12 марта 2011.
- ^ Hartmann, U., ed. (2000). Магнитные многослойные материалы и гигантское магнитосопротивление. Серия Спрингера по наукам о поверхности. Том 37. Спрингер. п. 111. ISBN 978-3-540-65568-8.
- ^ Третьяк, Львов и Барабанов 2002 С. 285–286.
- ^ Третьяк, Львов и Барабанов 2002 С. 289–291.
- ^ Зайцев, Д. «Магнетосопротивление, Туннельное». Словарь нанотехнологических и связанных с нанотехнологиями терминов. Роснано. Архивировано из оригинал 23 декабря 2011 г.. Получено 11 апреля 2011.
Библиография
- Байбич, М. Н .; Broto, J.M .; Fert, A .; Nguyen Van Dau, F .; Петров, Ф .; Etienne, P .; Creuzet, G .; Friederich, A .; Хазелас Дж. (1988). «Гигантское магнитосопротивление магнитных сверхрешеток (001) Fe / (001) Cr» (PDF). Письма с физическими проверками. 61 (21): 2472–2475. Bibcode:1988ПхРвЛ..61.2472Б. Дои:10.1103 / PhysRevLett.61.2472. PMID 10039127. Архивировано из оригинал (PDF) 21 января 2014 г.
- Бушоу, К. Х. Дж. (2005). Краткая энциклопедия магнитных и сверхпроводящих материалов (2-е изд.). Эльзевир. ISBN 978-008044586-1.
- Рейг, откровенный; Кардосо, Сусана; Мукхопадхьяй, Субхас Чандра (2013). Датчики гигантского магнитосопротивления (GMR) - от основы до современных приложений. Springer. Дои:10.1007/978-3-642-37172-1. ISBN 978-3-642-37171-4.
- Синдзё, Теруя (29 июня 2009 г.). Наномагнетизм и спинтроника. Эльзевир. ISBN 978-008093216-3.
- Третьяк, О.В .; Львов, В. А .; Барабанов, О. В. (2002). Физические основы спінової электроники [Физические основы спиновой электроники] (на украинском языке). Киевский университет. ISBN 966-594-323-5.
- Цымбал, Э.Ю .; Петтифор, Д. Г. (2001). «Перспективы гигантского магнитосопротивления». В Спапене, Франс; Зейтц, Фредерик; Тернбулл, Дэвид; Эренрайх, Генри (ред.). Физика твердого тела. Физика твердого тела: достижения в исследованиях и приложениях. Том 56. Academic Press. ISBN 978-012607756-8.
внешняя ссылка
- Гигантское магнитосопротивление: действительно большая идея за очень маленьким инструментом Национальная лаборатория сильного магнитного поля
- Презентация GMR-техники (IBM Research)

















