Модель Гудвина (экономика) - Goodwin model (economics)

В Модель Гудвинаиногда называют Модель классовой борьбы Гудвина, представляет собой модель эндогенных экономических колебаний, впервые предложенную американским экономистом Ричард М. Гудвин в 1967 году. Он сочетает в себе аспекты Harrod-Domar модель роста с Кривая Филлипса генерировать эндогенные циклы экономической активности (объем производства, безработица и заработная плата) в отличие от большинства современных макроэкономических моделей, в которых движения экономических агрегатов вызываются экзогенно предполагаемыми шоками. После публикации Гудвина в 1967 году эта модель была расширена и применена различными способами.

Модель

Объем производства определяется совокупной производственной функцией

${displaystyle q = min left (aell, {frac {k} {sigma}} ight)}$

куда:

q это совокупный выпуск

ℓ занятость труда

k (однородный) капитал

а производительность труда

σ коэффициент капитального выпуска, постоянная величина.

Все эти переменные являются функциями времени, хотя временные индексы для удобства опущены.

В отличие от модели Харрода – Домара предполагается полное использование капитала. Следовательно

${displaystyle aell = {frac {k} {sigma}} = q}$

во все времена. Уровень занятости определяется как

${displaystyle v = {frac {ell} {n}}}$

где п общая рабочая сила, которая растет со скоростью β. Дополнительно производительность труда а, предполагается, что также возрастает со скоростью α. Обратите внимание, что в этом случае темп роста уровня занятости определяется выражением

${displaystyle {frac {dv / dt} {v}} = g_ {v} = g_ {ell} - eta.}$

Темп роста абсолютного уровня занятости в свою очередь определяется выражением

${displaystyle {frac {dell / dt} {ell}} = g_ {ell} = g_ {q} -alpha}$

Предполагается, что заработная плата изменяется согласно линеаризованной Кривая Филлипса отношения, данные

${displaystyle {frac {dw / dt} {w}} = g_ {w} = ho v-gamma.}$

Другими словами, если рынок трудаплотно (занятость уже высока) существует повышательное давление на заработную плату, и наоборот на «слабом» рынке труда. Это аспект модели, который можно свободно связать с частью ее названия «классовая борьба», однако этот вид кривой Филлипса можно найти во многих макроэкономических моделях.

В доля рабочих в выпуске является ты, которая по определению

${displaystyle u = {frac {well} {q}} = {frac {w} {a}}.}$

Следовательно, темп роста доли рабочих составляет

${displaystyle {frac {du / dt} {u}} = g_ {u} = g_ {w} -alpha}$

Доля труда в выпуске увеличивается с ростом заработной платы, но снижается с ростом производительности, поскольку для производства того же объема продукции требуется меньше рабочих.

Наконец, у нас есть уравнение накопления капитала и результирующая скорость роста выпуска (поскольку k и q растут с одинаковой скоростью при предположении полного использования капитала и постоянной отдачи от масштаба). Предполагается, что рабочие потребляют свою заработную плату, а владельцы капитала откладывают часть своей прибыли (обратите внимание, что модель обобщается на случай, когда капиталисты экономят больше, чем рабочие), и что капитал обесценивается по дельте ставки. Темпы роста выпуска и капитала тогда определяются выражением

${displaystyle {frac {dk / dt} {k}} = g_ {k} = g_ {q} = s (1-u) (q / k) -delta.}$

Это, в свою очередь, означает, что

${displaystyle {frac {dv / dt} {v}} = g_ {v} = {frac {s (1-u)} {sigma}} - (delta + alpha + eta).}$

Решение

Два дифференциальных уравнения

${displaystyle {frac {dv / dt} {v}} = g_ {v} = {frac {s (1-u)} {sigma}} - (delta + alpha + eta)}$

${displaystyle {frac {du / dt} {u}} = g_ {u} = ho v-gamma -alpha}$

являются ключевыми уравнениями модели и фактически являются Уравнения Лотки – Вольтерра (которые используются в биологии для моделирования взаимодействия хищник-жертва).

Хотя модель может быть решена явно, поучительно проанализировать траекторию экономики с точки зрения фазовая диаграмма. Приравнивая два приведенных выше уравнения к нулю, мы получаем значения ты и v при котором рост v и рост тысоответственно равны нулю.

${displaystyle u * = 1- {frac {(delta + alpha + eta) sigma} {s}}}$

${displaystyle v * = {frac {gamma + alpha} {ho}}}$

Эти две линии (вместе с ограничениями на параметры, которые гарантируют, что ни u, ни v не могут превышать 1) делят положительный ортант на четыре области. На приведенном ниже рисунке стрелками показано движение экономики в каждом регионе. Например, в северо-западном регионе (высокая занятость, низкая доля рабочей силы в выпуске) экономика движется на северо-восток (занятость растет, доля рабочих увеличивается). Как только он пересечет линию u *, он начнет движение на юго-запад.

На приведенном ниже рисунке показано изменение потенциального выпуска (выпуск при полной занятости), фактического выпуска и заработной платы во времени.

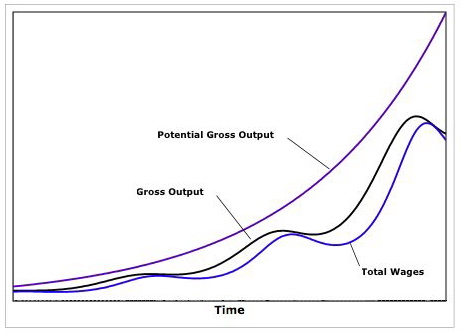
Как можно видеть, модель Гудвина может генерировать эндогенные колебания экономической активности, не полагаясь на посторонние предположения о внешних шоках, будь то со стороны спроса или предложения.

Модель применялась и расширялась многими экономистами с момента ее первого представления в 1967 году.

Статистика

• 

  Доля заработной платы (синяя линия) и гражданское коэффициент занятости населения (красная линия) в США
  Согласно модели Гудвина, следует ожидать, что доля заработной платы будет отставать от уровня занятости. Кажется, что это так, хотя бы из-за небольшой задержки во времени.

Смотрите также

• Бизнес цикл
• Ричард М. Гудвин
• Модель Харрода – Домара
• Марксистская экономика
• Кривая Филлипса

использованная литература

• Гудвин, Ричард М. (1967), «Цикл роста», в C.H. Файнштейн, редактор, Социализм, капитализм и экономический рост. Кембридж: Издательство Кембриджского университета.
• Гудвин, Ричард М., Хаотическая экономическая динамика, Oxford University Press, 1990.
• Флашель, Питер, Макродинамика капитализма - Элементы для синтеза Маркса, Кейнса и Шумпетера. Второе издание, Springer Verlag Berlin 2010. Глава 4.3.