Графическая динамическая система - Graph dynamical system

В математика, Концепция чего-либо графические динамические системы может использоваться для захвата широкого спектра процессов, происходящих в графах или сетях. Основная тема математического и вычислительного анализа GDS состоит в том, чтобы связать их структурные свойства (например, возможность подключения к сети) и возникающую в результате глобальную динамику.

В работе над GDS рассматриваются конечные графы и пространства с конечными состояниями. Таким образом, исследование обычно включает методы, например, теория графов, комбинаторика, алгебра, и динамические системы а не дифференциальная геометрия. В принципе, можно определить и изучить GDS над бесконечным графом (например, клеточные автоматы или же вероятностные клеточные автоматы над ${displaystyle mathbb {Z} ^ {k}}$ или же системы взаимодействующих частиц когда включена некоторая случайность), а также GDS с бесконечным пространством состояний (например, ${displaystyle mathbb {R}}$ как в решетках связанных карт); см., например, Wu.^[1] В дальнейшем все неявно предполагается конечным, если не указано иное.

Формальное определение

Графическая динамическая система состоит из следующих компонентов:

Конечная график Y с множеством вершин v [Y] = {1,2, ..., n}. В зависимости от контекста граф может быть направленным или неориентированным.
Штат Икс_v для каждой вершины v из Y взято из конечного множества K. В состояние системы это ппара Икс = (Икс₁, Икс₂, ... , Икс_п), и Икс[v] - набор, состоящий из состояний, связанных с вершинами в 1-окрестности v в Y (в фиксированном порядке).
А вершинная функция ж_v для каждой вершины v. Вершинная функция отображает состояние вершины v вовремя т в состояние вершины во время т + 1 на основе состояний, связанных с 1-окрестностью v в Y.
An схема обновления задающий механизм, с помощью которого выполняется отображение отдельных состояний вершины, чтобы вызвать дискретную динамическую систему с отображением F: K^п → K^п.

В фазовое пространство связанный с динамической системой с картой F: K^п → K^п конечный ориентированный граф с множеством вершин K^п и направленные края (Икс, F(Икс)). Структура фазового пространства определяется свойствами графа Y, вершинные функции (ж_я)_я, и схему обновления. Исследования в этой области направлены на определение свойств фазового пространства на основе структуры компонентов системы. Анализ носит локальный и глобальный характер.

Обобщенные клеточные автоматы (GCA)

Если, например, схема обновления состоит из синхронного применения вершинных функций, получается класс обобщенные клеточные автоматы (CA). В этом случае глобальная карта F: K^п → K^п дан кем-то

${displaystyle F (x) _ {v} = f_ {v} (x [v]) ;.}$

Этот класс называется обобщенными клеточными автоматами, поскольку классический или стандартный клеточные автоматы обычно определяются и изучаются на регулярных графах или сетках, а вершинные функции обычно считаются идентичными.

Пример: Позволять Y - круговой граф на вершинах {1,2,3,4} с ребрами {1,2}, {2,3}, {3,4} и {1,4}, обозначенный Circ₄. Позволять K = {0,1} - пространство состояний для каждой вершины и использовать функцию nor₃ : K³ → K определено ни₃(х, у, г) = (1 + Икс)(1 + у)(1 + z) с арифметикой по модулю 2 для всех вершинных функций. Затем, например, состояние системы (0,1,0,0) отображается в (0, 0, 0, 1) с использованием синхронного обновления. Все переходы показаны в фазовом пространстве ниже.

326

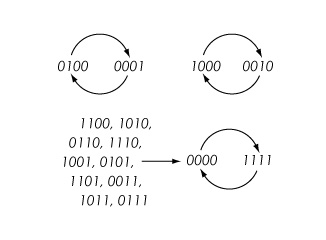
Последовательные динамические системы (SDS)

Если вершинные функции применяются асинхронно в последовательности, указанной словом ш = (ш₁, ш₂, ... , ш_м) или перестановка ${displaystyle pi}$ = ( ${displaystyle pi _ {1}}$ , ${displaystyle pi _ {2}, точки, pi _ {n}}$ ) из v[Y] получается класс Последовательные динамические системы (SDS).^[2] В этом случае удобно ввести Y-местные карты F_я построенный из вершинных функций

{displaystyle F_ {i} (x) = (x_ {1}, x_ {2}, ldots, x_ {i-1}, f_ {i} (x [i]), x_ {i + 1}, ldots, x_ {n}) ;.}

Карта SDS F = [F_Y , ш] : K^п → K^п композиция функций

{displaystyle [F_ {Y}, w] = F_ {w (m)} circ F_ {w (m-1)} circ cdots circ F_ {w (2)} circ F_ {w (1)} ;.}

Если последовательность обновления представляет собой перестановку, часто говорят о SDS перестановки чтобы подчеркнуть этот момент.

Пример: Позволять Y - круговой граф на вершинах {1,2,3,4} с ребрами {1,2}, {2,3}, {3,4} и {1,4}, обозначенный Circ₄. Позволять K= {0,1} - пространство состояний для каждой вершины и использовать функцию nor₃ : K³ → K определено ни₃(х, у, г) = (1 + Икс)(1 + у)(1 + z) с арифметикой по модулю 2 для всех вершинных функций. Используя последовательность обновления (1,2,3,4), состояние системы (0, 1, 0, 0) отображается в (0, 0, 1, 0). Все переходы состояний системы для этой последовательной динамической системы показаны в фазовом пространстве ниже.

326

Стохастические графические динамические системы

Например, с точки зрения приложений интересно рассмотреть случай, когда один или несколько компонентов GDS содержат стохастические элементы. Мотивационные приложения могут включать в себя процессы, которые не до конца поняты (например, динамика внутри ячейки), и где определенные аспекты для всех практических целей, похоже, ведут себя в соответствии с некоторым распределением вероятностей. Есть также приложения, основанные на детерминированных принципах, описание которых настолько сложно или громоздко, что имеет смысл рассматривать вероятностные приближения.

Каждый элемент графической динамической системы можно сделать стохастическим несколькими способами. Например, в последовательной динамической системе последовательность обновления может быть сделана стохастической. На каждой итерации можно выбрать последовательность обновления ш случайным образом из заданного распределения последовательностей обновления с соответствующими вероятностями. Соответствующее вероятностное пространство обновленных последовательностей порождает вероятностное пространство SDS-карт. Естественным объектом для изучения в этом отношении является Цепь Маркова на пространстве состояний, индуцированном этим набором карт SDS. Этот случай упоминается как последовательность обновления стохастической GDS и мотивируется, например, процессами, в которых «события» происходят случайным образом в соответствии с определенными скоростями (например, химическими реакциями), синхронизацией в параллельных вычислениях / симуляциях дискретных событий и в вычислительных парадигмах, описанных ниже.

Этот конкретный пример со стохастической последовательностью обновления иллюстрирует два общих факта для таких систем: переход к динамической системе со стохастическим графом обычно приводит к (1) изучению цепей Маркова (с конкретной структурой, управляемой составляющими GDS) и (2) результирующие цепи Маркова имеют тенденцию быть большими и иметь экспоненциальное число состояний. Центральная цель исследования стохастической GDS - получить редуцированные модели.

Можно также рассмотреть случай, когда вершинные функции являются стохастическими, т. Е. функция стохастической GDS. Например, Random Булевы сети являются примерами стохастической GDS функции, использующей схему синхронного обновления и где пространство состояний K = {0, 1}. Конечный вероятностные клеточные автоматы (PCA) - еще один пример функции стохастической GDS. В принципе, класс систем взаимодействующих частиц (IPS) охватывает конечные и бесконечные PCA, но на практике работа над IPS в основном связана с бесконечным случаем, поскольку это позволяет вводить более интересные топологии в пространстве состояний.

Приложения

Графические динамические системы представляют собой естественную основу для описания распределенных систем, таких как биологические сети и эпидемии в социальных сетях, многие из которых часто называют сложными системами.

Смотрите также

дальнейшее чтение

Маколей, Мэтью; Мортвейт, Хеннинг С. (2009). «Циклическая эквивалентность графических динамических систем». Нелинейность. 22 (2): 421–436. arXiv:0802.4412. Bibcode:2009Nonli..22..421M. Дои:10.1088/0951-7715/22/2/010.
Голубицкий, Мартин; Стюарт, Ян (2003). Перспектива симметрии. Базель: Биркхаузер. ISBN 0-8176-2171-7.

внешняя ссылка

Графические динамические системы - математическая основа для систем, основанных на взаимодействии, их анализ и моделирование, Хеннинг Мортвейт

[wu-05-1] Ву, Чай Ва (2005). «Синхронизация в сетях нелинейных динамических систем, связанных ориентированным графом». Нелинейность. 18 (3): 1057–1064. Bibcode:2005Nonli..18.1057W. Дои:10.1088/0951-7715/18/3/007.

[Mortveit-08-2] Mortveit, Henning S .; Рейдис, Кристиан М. (2008). Введение в последовательные динамические системы. Universitext. Нью-Йорк: Springer Verlag. ISBN 978-0-387-30654-4.

[1]

[2]