Гипогамильтонов граф - Википедия - Hypohamiltonian graph
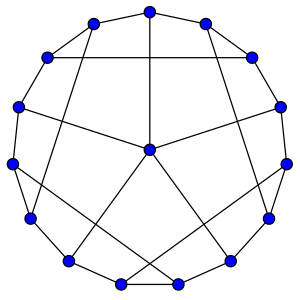
В математической области теория графов, график грамм как говорят гипогамильтониан если грамм сам по себе не имеет Гамильтонов цикл но каждый граф, образованный удалением одной вершины из грамм является Гамильтониан.
История
Гипогамильтоновы графы впервые были изучены Сусселье (1963). Линдгрен (1967) цитирует Годен, Герц и Росси (1964) и Бусакер и Саати (1965) как дополнительные ранние статьи по теме; еще одна ранняя работа Герц, Дуби и Виге (1967).
Грёчель (1980) резюмирует большую часть исследований в этой области следующим предложением: «Статьи, посвященные этим графам ... обычно демонстрируют новые классы гипогамильтоновых или гипотетических графов, показывающие, что для определенных порядков п такие графы действительно существуют или обладают странными и неожиданными свойствами ».
Приложения
Гипогамильтоновы графы возникают в целочисленное программирование решения для задача коммивояжера: некоторые виды гипогамильтоновых графов определяют грани из многогранник коммивояжер, фигура, определяемая как выпуклый корпус множества возможных решений задачи коммивояжера, и эти грани могут быть использованы в режущие методы для решения проблемы.[1] Грёчель (1980) отмечает, что вычислительная сложность определения того, является ли граф гипогамильтоновым, хотя и неизвестно, скорее всего, будет высоким, что затрудняет поиск граней этих типов, за исключением тех, которые определяются небольшими гипогамильтоновыми графами; к счастью, самые маленькие графы приводят к сильнейшим неравенствам для этого приложения.[2]
Понятия, тесно связанные с гипогамильтонностью, также использовались Пак, Лим и Ким (2007) измерить Отказоустойчивость из сетевые топологии за параллельные вычисления.
Характеристики
Каждый гипогамильтонов граф должен быть 3-вершинно-связанный, так как удаление любых двух вершин оставляет гамильтонов путь, который связан. Существуют п-вершинные гипогамильтоновы графы с максимальной степенью п/ 2, и в котором примерно п2/ 4 ребра.[3]

Герц, Дуби и Виге (1967) предположил, что каждый гипогамильтонов граф имеет обхват 5 и более, но это было опровергнуто Томассен (1974b), который нашел примеры с обхватом 3 и 4. Некоторое время было неизвестно, может ли гипогамильтонов граф планарный, но теперь известно несколько примеров,[4] самая маленькая из которых имеет 40 вершин.[5] Каждый плоский гипогамильтонов граф имеет хотя бы одну вершину с тремя инцидентными ребрами.[6]
Если 3-регулярный граф гамильтониан, его края можно раскрашивать с тремя цветами: используйте чередующиеся цвета для ребер в гамильтоновом цикле (который должен иметь одинаковую длину на лемма о рукопожатии ) и третий цвет для всех остальных краев. Поэтому все язвы кубические графы без мостов, требующие четырех цветов ребер, должны быть негамильтоновыми, а многие известные снарки являются гипогамильтоновыми. Каждый гипогамильтоновский снарк бикритический: удаление любых двух вершин оставляет подграф, края которого можно раскрасить только в три цвета.[7] Трехкратную раскраску этого подграфа можно описать просто: после удаления одной вершины оставшиеся вершины содержат гамильтонов цикл. После удаления второй вершины этот цикл становится путем, края которого можно раскрасить, чередуя два цвета. Остальные ребра образуют соответствие и может быть окрашен в третий цвет.
Цветовые классы любой 3-раскраски ребер 3-регулярного графа образуют три паросочетания, так что каждое ребро принадлежит ровно одному из паросочетаний. Гипогамильтоновы снарки не имеют разбиения на паросочетания этого типа, но Хэггквист (2007) предполагает, что ребра любого гипогамильтонова снарка могут быть использованы для образования шести паросочетаний, так что каждое ребро принадлежит ровно двум из паросочетаний. Это частный случай гипотезы Берге – Фулкерсона о том, что любой снарк имеет шесть паросочетаний с этим свойством.
Гипогамильтоновы графы не могут быть двудольными: в двудольном графе вершина может быть удалена для образования гамильтонова подграфа, только если она принадлежит большему из двух цветовых классов графа. Однако каждый двудольный граф происходит как индуцированный подграф некоторого гипогамильтонова графа.[8]
Примеры
Наименьший гипогамильтонов граф - это Граф Петерсена (Герц, Дуби и Виге 1967 ). В более общем плане обобщенный граф Петерсена GP (п, 2) является гипогамильтоновой, когда п равно 5 (mod 6);[9] граф Петерсена является примером этой конструкции с п = 5.
Линдгрен (1967) нашел еще один бесконечный класс гипогамильтоновых графов с числом вершин 4 (mod 6). Конструкция Линдгрена состоит из цикла длины 3 (mod 6) и единственной центральной вершины; центральная вершина соединяется с каждой третьей вершиной цикла ребрами, которые он называет спицами, а вершины, находящиеся на расстоянии двух позиций от каждой конечной точки спицы, соединяются друг с другом. Опять же, самым маленьким примером конструкции Линдгрена является граф Петерсена.
Дополнительные бесконечные семейства даются Бонди (1972), Дуайен и ван Дист (1975), и Гутт (1977).
Перечисление
Вацлав Хваталь в 1973 г. доказал, что для всех достаточно больших п существует гипогамильтонов граф с п вершины. Принимая во внимание последующие открытия,[10] «Достаточно большой», как теперь известно, означает, что такие графы существуют для всех п ≥ 18. Известен полный список гипогамильтоновых графов с не более чем 17 вершинами:[11] это 10-вершинный граф Петерсена, 13-вершинный граф и 15-вершинный граф, найденные компьютерным поиском Герц (1968), и четыре 16-вершинных графа. Существует не менее тринадцати гипогамильтоновых графов с 18 вершинами. Применяя триггерный метод Хваталь (1973) графу Петерсена и цветок snark, можно показать, что количество гипогамильтоновых графов, а точнее, количество гипогамильтоновых снарков, растет как экспоненциальная функция от количества вершин.[12]
Обобщения
Теоретики графов также изучали графики с возможностью отслеживания, графы, не содержащие гамильтонова пути, но такие, что каждое подмножество п - 1 вершину можно соединить путем.[13] Аналогичные определения гипогамильтоничности и гипотезы для ориентированные графы были рассмотрены несколькими авторами.[14]
Эквивалентное определение гипогамильтоновых графов состоит в том, что их самый длинный цикл имеет длину п - 1 и что пересечение всех самых длинных циклов пусто. Менке, Замфиреску и Замфиреску (1998) исследовать графы с тем же свойством, что пересечение самых длинных циклов пусто, но в которых длина самого длинного цикла короче, чем п − 1. Герц (1968) определяет цикличность графа как наибольшее число k так что каждый k вершины принадлежат циклу; гипогамильтоновы графы - это именно те графы, которые имеют циклируемость п - 1. Аналогично, Пак, Лим и Ким (2007) определить граф как ƒ-гамильтониан разлома если удаление не более вершин оставляет гамильтонов подграф. Шауэрте и Замфиреску (2006) изучать графики с цикличностью п − 2.
Примечания
- ^ Грёчель (1977); Грёчель (1980); Грётчель и Вакабаяши (1981).
- ^ Goemans (1995).
- ^ Томассен (1981).
- ^ Существование плоских гипогамильтоновых графов было поставлено как открытый вопрос Хваталь (1973), и Хватал, Кларнер и Кнут (1972) предложили приз в 5 долларов за строительство одного. Томассен (1976) использовал Теорема Гринберга найти планарные гипогамильтоновы графы с обхватом 3, 4 и 5 и показал, что существует бесконечно много плоских гипогамильтоновых графов.
- ^ Jooyandeh et al. (2013), используя компьютерный поиск и теорему Гринберга. Ранее небольшие плоские гипогамильтоновы графы с 42, 57 и 48 вершинами соответственно были найдены Винер и Арая (2009), Хацель (1979) и Замфиреску и Замфиреску (2007).
- ^ Томассен (1978).
- ^ Штеффен (1998); Штеффен (2001).
- ^ Кольер и Шмейхель (1977).
- ^ Робертсон (1969) доказано, что эти графы негамильтоновы, в то время как несложно проверить, что их удаления с одной вершиной являются гамильтоновыми. Видеть Альспах (1983) для классификации негамильтоновых обобщенных графов Петерсена.
- ^ Томассен (1974a); Дуайен и ван Дист (1975).
- ^ Олдред, Маккей и Вормолд (1997). Также (последовательность A141150 в OEIS ).
- ^ Скупень (1989); Скупень (2007).
- ^ Капур, Кронк и Лик (1968); Кронк (1969); Грюнбаум (1974); Томассен (1974a).
- ^ Фуке и Жоливе (1978); Грётчель и Вакабаяши (1980); Грётчель и Вакабаяши (1984); Томассен (1978).
Рекомендации
- Aldred, R.A .; Маккей, Б.Д.; Вормолд, Н. К. (1997), «Малые гипогамильтоновы графы» (PDF), J. Комбинаторная математика. Комбинаторные вычисления., 23: 143–152.
- Альспах, Б. (1983), "Классификация гамильтоновых обобщенных графов Петерсена", Журнал комбинаторной теории, серия B, 34 (3): 293–312, Дои:10.1016/0095-8956(83)90042-4, МИСТЕР 0714452.
- Бонди, Дж. А. (1972), "Вариации гамильтоновой темы", Канадский математический бюллетень, 15: 57–62, Дои:10.4153 / CMB-1972-012-3.
- Busacker, R.G .; Саати, Т. Л. (1965), Конечные графы и сети, Макгроу-Хилл.
- Хватал, В. (1973), «Триггеры в гипогамильтоновых графах», Канадский математический бюллетень, 16: 33–41, Дои:10.4153 / CMB-1973-008-9, МИСТЕР 0371722.
- Хватал, В.; Кларнер, Д. А .; Кнут, Д. Э. (1972), Избранные комбинаторные задачи исследования (PDF), Тех. Отчет STAN-CS-72-292, факультет компьютерных наук, Стэнфордский университет.
- Collier, J. B .; Шмейхель, Э. Ф. (1977), "Новые конструкции триггеров для гипогамильтоновых графов", Дискретная математика, 18 (3): 265–271, Дои:10.1016 / 0012-365X (77) 90130-3, МИСТЕР 0543828.
- Doyen, J .; Ван Дист В. (1975), "Новые семейства гипогамильтоновых графов", Дискретная математика, 13 (3): 225–236, Дои:10.1016 / 0012-365X (75) 90020-5, МИСТЕР 0416979.
- Fouquet, J.-L .; Жоливе, Дж. Л. (1978), "Гипогамильтоновы ориентированные графы", Cahiers Center Études Rech. Opér., 20 (2): 171–181, МИСТЕР 0498218.
- Gaudin, T .; Herz, P .; Росси (1964), "Решение проблемы № 29", Преподобный Franç. Речь. Операционнель, 8: 214–218.
- Goemans, Мишель X. (1995), "Сравнение наихудшего случая допустимых неравенств для TSP", Математическое программирование, 69 (1–3): 335–349, CiteSeerX 10.1.1.52.8008, Дои:10.1007 / BF01585563.
- Грётшель, М. (1977), "Гипогамильтоновы грани симметричного многогранника коммивояжера", Zeitschrift für Angewandte Mathematik und Mechanik, 58: 469–471.
- Грётшель, М. (1980), "О монотонной симметричной задаче коммивояжера: гипогамильтоновы / гипотетические графы и фасеты", Математика исследования операций, 5 (2): 285–292, Дои:10.1287 / moor.5.2.285, JSTOR 3689157.
- Грётшель, М.; Вакабаяси Ю. (1980), «Гипогамильтоновы орграфы», Методы исследования операций, 36: 99–119, Zbl 0436.05038.
- Грётшель, М.; Вакабаяси Ю. (1981), "О структуре монотонного асимметричного многогранника коммивояжера I: гипогамильтоновы грани", Дискретная математика, 24: 43–59, Дои:10.1016 / 0012-365X (81) 90021-2.
- Грётшель, М.; Wakabayashi, Y. (1984), "Конструкции предполагаемых орграфов", в Cottle, R.W .; Kelmanson, M. L .; Корте, Б. (ред.), Математическое программирование (Материалы Международного конгресса, Рио-де-Жанейро, 1981 г.), Северная Голландия.
- Грюнбаум, Б. (1974), «Вершины, пропущенные самыми длинными путями или цепями», Журнал комбинаторной теории, серия А, 17: 31–38, Дои:10.1016/0097-3165(74)90025-9, МИСТЕР 0349474.
- Гутт, Симона (1977), "Бесконечные семейства гипогамильтоновых графов", Королевская академия Бельгии, Bulletin de la Classe des Sciences, 5e Série, 63 (5): 432–440, МИСТЕР 0498243.
- Хэггквист, Р. (2007), Мохар, Б.; Новаковски, Р. Дж .; Вест, Д. Б. (ред.), «Проблема 443. Частный случай гипотезы Фулкерсона», Проблемы исследования 5-й словенской конференции (Блед, 2003), Дискретная математика, 307 (3–5): 650–658, Дои:10.1016 / j.disc.2006.07.013.
- Hatzel, W. (1979), "Ein planarer hypohamiltonscher Graph mit 57 Knoten", Математика. Анна., 243 (3): 213–216, Дои:10.1007 / BF01424541, МИСТЕР 0548801.
- Герц, Дж. К. (1968), "Sur la cyclabilité des graphes", Компьютеры в математических исследованиях, Северная Голландия, стр. 97–107, МИСТЕР 0245461.
- Herz, J. C .; Duby, J. J .; Vigué, F. (1967), "Recherche systématique des graphes hypohamiltoniens", в Розенштиль, П. (ред.), Теория графов: Международный симпозиум, Рим, 1966 г., Paris: Gordon and Breach, стр. 153–159..
- Джуйанде, Мохаммадреза; Маккей, Брендан Д.; Östergård, Patric R.J .; Pettersson, Ville H .; Замфиреску, Кэрол Т. (2013), Плоские гипогамильтоновы графы на 40 вершинах, arXiv:1302.2698, Bibcode:2013arXiv1302.2698J.
- Капур, С. Ф .; Kronk, H.V .; Лик, Д. Р. (1968), «Об обходных путях в графах», Канадский математический бюллетень, 11 (2): 195–201, Дои:10.4153 / CMB-1968-022-8, МИСТЕР 0229543.
- Кронк, Х. В. (1969), Клее, В. (ред.), «Существует ли граф, по которому можно отследить гипотезу?», «Проблемы исследования», Американский математический ежемесячный журнал, 76 (7): 809–810, Дои:10.2307/2317879, JSTOR 2317879.
- Линдгрен, В. Ф. (1967), "Бесконечный класс гипогамильтоновых графов", Американский математический ежемесячный журнал, 74 (9): 1087–1089, Дои:10.2307/2313617, JSTOR 2313617, МИСТЕР 0224501.
- Máčajová, E .; Шковьера, М. (2007), «Построение гипогамильтоновых снарков с циклической связностью 5 и 6», Электронный журнал комбинаторики, 14 (1): R14.
- Menke, B .; Zamfirescu, T. I .; Замфиреску, К. М. (1998), "Пересечения самых длинных циклов в сеточных графах", Журнал теории графов, 25 (1): 37–52, Дои:10.1002 / (SICI) 1097-0118 (199705) 25: 1 <37 :: AID-JGT2> 3.0.CO; 2-J.
- Mohanty, S.P .; Рао, Д. (1981), "Семейство гипогамильтоновых обобщенных призм", Комбинаторика и теория графов, Конспект лекций по математике, 885, Springer-Verlag, стр. 331–338, Дои:10.1007 / BFb0092278, ISBN 978-3-540-11151-1.
- Park, J.-H .; Lim, H.-S .; Ким, Х.-К. (2007), "Пан-связность и панцикличность гиперкубоподобных сетей межсоединений с неисправными элементами", Теоретическая информатика, 377 (1–3): 170–180, Дои:10.1016 / j.tcs.2007.02.029.
- Робертсон, Г. Н. (1969), Графики минимальные ограничения подпруги, валентности и связности, Докторская диссертация, Ватерлоо, Онтарио: Университет Ватерлоо.
- Шауэрте, Борис; Замфиреску, К. Т. (2006), «Регулярные графы, в которых каждая пара точек пропускается некоторым самым длинным циклом», An. Univ. Craiova Ser. Мат. Сообщить., 33: 154–173, МИСТЕР 2359901.
- Скупень, З. (1989), "Экспоненциально много гипогамильтоновых графов", Графы, гиперграфы и матроиды III (Proc. Conf. Kalsk 1988), Зелена-Гура: Высший инженерный колледж, стр. 123–132.. Как цитирует Скупень (2007).
- Skupień, Z. (2007), "Экспоненциально много гипогамильтоновых снарков", 6-й Чешско-словацкий международный симпозиум по комбинаторике, теории графов, алгоритмам и приложениям, Электронные заметки по дискретной математике, 28, стр. 417–424, Дои:10.1016 / j.endm.2007.01.059.
- Сусселье, Р. (1963), Берге, К. (ред.), "Problème № 29: Le cercle des irascibles", Problèmes plaisants et délectables, Преподобный Franç. Речь. Операционнель, 7: 405–406.
- Штеффен, Э. (1998), "Классификация и характеристики снарков", Дискретная математика, 188 (1–3): 183–203, Дои:10.1016 / S0012-365X (97) 00255-0, МИСТЕР 1630478.
- Штеффен, Э. (2001), "О бикритических снарках", Математика. Словака, 51 (2): 141–150, МИСТЕР 1841443.
- Томассен, Карстен (1974a), «Гипогамильтоновы графы и графы с возможностью отслеживания», Дискретная математика, 9: 91–96, Дои:10.1016 / 0012-365X (74) 90074-0, МИСТЕР 0347682.
- Томассен, Карстен (1974b), «О гипогамильтоновых графах», Дискретная математика, 10 (2): 383–390, Дои:10.1016 / 0012-365X (74) 90128-9, МИСТЕР 0357226.
- Томассен, Карстен (1976), «Плоские и бесконечные гипогамильтоновы графы с возможностью отслеживания», Дискретная математика, 14 (4): 377–389, Дои:10.1016 / 0012-365X (76) 90071-6, МИСТЕР 0422086.
- Томассен, Карстен (1978), «Гипогамильтоновы графы и орграфы», Теория и приложения графов (Proc. Internat. Conf., Western Mich. Univ., Kalamazoo, Mich., 1976), Конспект лекций по математике, 642, Берлин: Springer-Verlag, стр. 557–571, МИСТЕР 0499523.
- Томассен, Карстен (1981), "Плоские кубические гипогамильтонианы и отслеживаемые графы", Журнал комбинаторной теории, серия B, 30: 36–44, Дои:10.1016/0095-8956(81)90089-7, МИСТЕР 0609592.
- Винер, Габор; Арая, Макото (2009), Главный вопрос, arXiv:0904.3012, Bibcode:2009arXiv0904.3012W.
- Zamfirescu, C.T .; Замфиреску, Т. И. (2007), "Планарный гипогамильтонов граф с 48 вершинами", Журнал теории графов, 55 (4): 338–342, Дои:10.1002 / jgt.20241.
