Равнобедренный набор - Isosceles set

Уникальное 6-точечное равнобедренное тело, расположенное в плоскости. Заштрихованные области показывают четыре из 20 равнобедренных треугольников, образованных тройками этих точек.

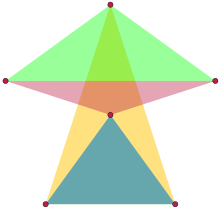
В дискретная геометрия, равнобедренный набор представляет собой набор точек, каждые три из которых образуют равнобедренный треугольник. Точнее, каждые три точки должны определять не более двух расстояний; это также позволяет выродиться равнобедренные треугольники, образованные тремя одинаково расположенными точками на прямой.

Задача поиска наибольшего равнобедренного множества в Евклидово пространство данного измерения был поставлен в 1946 г. Пол Эрдёш. В своей формулировке проблемы Эрдеш заметил, что наибольшее такое множество в Евклидова плоскость имеет шесть очков.^[1] В своем решении 1947 года Лерой Милтон Келли более убедительно показали, что единственное шеститочечное плоское равнобедренное множество состоит из вершин и центра правильный пятиугольник. В трех измерениях Келли нашла равнобедренный набор из восьми точек, шесть из которых совпадают; оставшиеся две точки лежат на линии, перпендикулярной пятиугольнику, проходящей через его центр, на том же расстоянии, что и вершины пятиугольника от центра.^[2] Позже было доказано, что этот трехмерный пример является оптимальным и единственным оптимальным решением.^[3][4]

В ${ displaystyle d}$-мерное пространство, равнобедренный набор может иметь не более

${ displaystyle { binom {d + 2} {2}}}$

точки.^[5] Это трудно для ${ displaystyle d = 6}$ и для ${ displaystyle d = 8}$ но не обязательно для других размеров. Максимальное количество точек в ${ displaystyle d}$-мерный равнобедренный набор, для ${ Displaystyle d = 1,2, точки, 8}$, как известно,^[6]

3, 6, 8, 11, 17, 28, 30, 45 (последовательность A175769 в OEIS )

но эти числа не известны для высших измерений.^[7]

Эту же проблему можно рассмотреть и для других метрические пространства. Например, для Пространства Хэмминга известны несколько меньшие оценки сверху, чем для евклидовых пространств той же размерности.^[7] В ультраметрическое пространство, все пространство (и любое его подмножество) является равнобедренным множеством. Поэтому ультраметрические пространства иногда называют равнобедренными. Однако не каждый равнобедренный набор ультраметрический; например, тупые равнобедренные евклидовы треугольники не являются ультраметричными.^[8]

Рекомендации