Анализ дерева предметов - Item tree analysis
Анализ дерева предметов (ITA) это данные аналитические метод, позволяющий построить иерархическую структуру по элементам опросник или же тест от наблюдаемых моделей ответа.
Предположим, что у нас есть анкета с м элементы, и субъекты могут отвечать положительно (1) или отрицательно (0) на каждый из этих элементов, т.е.дихотомический. Если п испытуемые отвечают на вопросы, в результате чего двоичный данные матрица Dс м колонны и п Типичные примеры этого формата данных - тестовые задания, которые испытуемые могут решить (1) или не выполнить (0). Другими типичными примерами являются анкеты, в которых вопросы представляют собой утверждения, с которыми испытуемые могут согласиться (1) или не согласиться (0).
В зависимости от содержания элементов возможно, что ответ субъекта на элемент j определяет ее или его ответы на другие вопросы. Например, возможно, что каждый субъект соглашается с пунктом j также согласен с пунктом я. В этом случае мы говорим, что пункт j подразумевает элемент я (короткая ). Цель ITA - выявить такиедетерминированный последствия от набор данных D.
Алгоритмы для ITA
ITA была первоначально разработана Ван Леуве в 1974 году.[1] Результат его алгоритм, который в дальнейшем мы будем называть Классическая ITA, это логически последовательный набор импликаций . Логически непротиворечивый означает, что если я подразумевает j и j подразумевает k тогда я подразумевает k за каждую тройку я, j, k пунктов. Таким образом, результатом ITA является рефлексивный и переходный отношение на наборе элементов, т.е. квазипорядок по предметам.
Другой алгоритм выполнения ITA был предложен в Шрепп (1999). Этот алгоритм называется Индуктивный ITA.
И классический ITA, и индуктивный ITA создают квазипорядок на элементе, установленном разведочный анализ данных. Но оба метода используют разные алгоритмы для построения этого квазипорядка. Для данного набора данных результирующие квазипорядки от классической и индуктивной ITA обычно будут различаться.
Подробное описание алгоритмов, используемых в классической и индуктивной ITA, можно найти в Шрепп (2003) или же Шрепп (2006)[1]. В недавней статье (Sargin & Ünlü, 2009) предлагаются некоторые модификации алгоритма индуктивной ITA, которые улучшают способность этого метода обнаруживать правильные последствия из данных (особенно в случае более высоких показателей ошибок случайного ответа).
Отношение к другим методам
ITA относится к группе методов анализа данных, называемых Булев анализ анкет.Логический анализ был представлен Flament в 1976 году.[2] Целью логического анализа является обнаружение детерминированных зависимостей (формулы из Логическая логика соединение предметов, например, , , и ) между пунктами анкеты или теста. Фламент (1976) разработан ряд различных методов логического анализа. См., Например, Ван Буггенхаут и Дегреф (1987), Duquenne (1987) или же Теунс (1994).Эти методы разделяют цель выводить детерминированные зависимости между элементами анкеты от данных, но разные алгоритмы для достижения этой цели. Сравнение ITA с другими методами анализа логических данных можно найти в Шрепп (2003).
Приложения
Доступно несколько исследовательских работ, в которых описаны конкретные применения анализа дерева элементов. Хелд и Короссы (1998) анализирует влияние на набор алгебра проблемы с классическим ITA. Анализ дерева предметов также используется в ряде социальные науки получить на виду в структуру дихотомических данных. В Барт и Крус (1973)Например, предшественник ITA используется для установления иерархического порядка по элементам, которые описывают социально неприемлемое поведение. В Янссенс (1999) используется метод булевого анализа для исследования процесса интеграции меньшинства в система ценностей доминирующей культуры. Шрепп[3] описывает несколько применений индуктивной ITA в анализе зависимостей между пунктами анкет по общественным наукам.
Пример заявки
Чтобы показать возможности анализа набора данных ITA, мы анализируем формулировки вопроса 4 Международной программы исследований в области социальных наук (ISSSP) за 1995 год с помощью индуктивной и классической ITA. ISSSP представляет собой продолжающуюся ежегодную программу перекрестных исследований. национальное сотрудничество в проведении опросов, охватывающих важные темы для исследований в области социальных наук. Программа ежегодно проводит один опрос с сопоставимыми вопросами в каждой из участвующих стран. Тема обзора 1995 г. национальная принадлежность. Мы анализируем результаты для вопроса 4 для набора данных Западная Германия Утверждение для вопроса 4 было:
Некоторые люди говорят, что для того, чтобы быть настоящим немцем, важно следующее. Другие говорят, что они не важны. Как вы думаете, насколько важным является каждое из следующих:
1. быть рожденным в Германии
2. иметь немецкое гражданство
3. прожить в Германии большую часть жизни
4. уметь говорить по-немецки
5. быть христианином
6. уважать политические институты Германии
7. чувствовать себя немцем
У испытуемых были возможности ответа Очень важно, Важный, Не очень важно, Совсем не важно, и Не могу выбрать ответить на утверждения. Чтобы применить ITA к этому набору данных, мы изменили категории ответов.
Очень важно и Важный имеют код 1. Не очень важно и Совсем не важно кодируются как 0. Не могу выбрать был обработан как отсутствующие данные.
На следующем рисунке показаны результирующие квази-порядки. от индуктивного ITA и из классической ITA.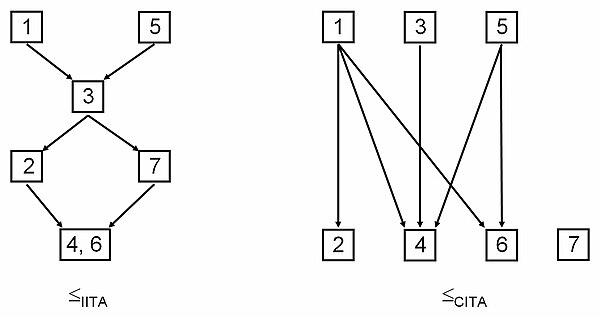
Доступное программное обеспечение
Программа ITA 2.0 реализует как классическую, так и индуктивную ITA. Программа доступна на [2]. Краткая документация программы доступна на [3].
Смотрите также
Примечания
Рекомендации
- Барт, В. М. и Крус, Д. Дж. (1973). Теоретико-упорядоченный метод определения иерархии элементов. Образовательно-психологическое измерение, 33, 291-300.
- Duquenne V (1987). Концептуальные значения между атрибутами и некоторыми свойствами представления для конечных решеток. В B Ganter, R Wille, K Wolfe (ред.), Beiträge zur Begriffsanalyse: Vorträge der Arbeitstagung Begriffsanalyse, Дармштадт 1986, стр. 313–339. Wissenschafts-Verlag, Мангейм.
- Flament C (1976). L’Analyse Bool´eenne de Questionnaire. Мутон, Париж.
- Хелд, Т., и Коросси, К. (1998). Анализ данных как эвристика для установления теоретически обоснованных структур элементов. Zeitschrift für Psychologie, 206, 169–188.
- Янссенс Р. (1999). Булевский подход к измерению групповых процессов и отношений. Концепция интеграции в качестве примера. Математические социальные науки, 38, 275-293.
- Шрепп М (1999). Об эмпирическом построении импликаций на двузначные тестовые задания. Математические социальные науки, 38 (3), 361–375.
- Шрепп, М (2002). Исследовательский анализ эмпирических данных путем булевого анализа анкет. Zeitschrift für Psychologie, 210/2, S. 99-109.
- Шрепп, М. (2003). Метод анализа иерархических зависимостей между элементами анкеты. Методы психологического исследования, 19, 43-79.
- Шрепп, М. (2006). ITA 2.0: программа для классического и индуктивного анализа дерева предметов. Журнал статистического программного обеспечения, Vol. 16, выпуск 10.
- Шрепп, М. (2006). Свойства коэффициента корреляционного согласия: комментарий к Ünlü & Albert (2004). Математические социальные науки, Vol. 51, выпуск 1, 117-123.
- Шрепп М. (2007). Об оценке мер соответствия для квази-заказов. Математические социальные науки Vol. 53, Выпуск 2, 196-208.
- Теунс П. (1994). Метод дихотомизации для булевого анализа количественных данных о взаимодействии. В G Fischer, D. Laming (eds.), Contributions to Mathematical Psychology, Psychometrics and Methodology, Scientific Psychology Series, pp. 173–194. Спрингер-Верлаг, Нью-Йорк.
- Юнлю, А., и Альберт, Д. (2004). Коэффициент корреляционного согласия CA - математический анализ описательной меры согласия. Математические социальные науки, 48, 281–314.
- Ван Буггенхаут Дж, Степень Е. (1987). О методах дихотомизации в булевом анализе анкет. В Э. Роскам, Р. Сак (ред.), «Математическая психология в прогрессе», издательство Elsevier Science Publishers B.V., Северная Голландия.
- Ван Леуве, J.F.J. (1974). Анализ дерева предметов. Nederlands Tijdschrift voor de Psychologie, 29, 475-484.
- Саргин, А., & Юнлю, А. (2009). Индуктивный анализ дерева элементов: исправления, улучшения и сравнения. Математические социальные науки, 58, 376–392.





