Карта Карно - Karnaugh map

эта статья может быть расширен текстом, переведенным с соответствующая статья на немецком. (Февраль 2018 г.) Щелкните [показать] для получения важных инструкций по переводу. Посмотреть Машинный перевод статьи на немецкий язык. Машинный перевод нравится DeepL или Гугл переводчик является полезной отправной точкой для переводов, но переводчики должны исправлять ошибки по мере необходимости и подтверждать точность перевода, а не просто копировать и вставлять машинно переведенный текст в английскую Википедию. Не переводите текст, который кажется ненадежным или некачественным. Если возможно, сверьте текст со ссылками, приведенными в статье на иностранном языке. Ты должен предоставлять авторское право в редактировать резюме сопровождая ваш перевод, предоставив межъязыковая ссылка к источнику вашего перевода. Сводка редактирования атрибуции модели Содержимое этой редакции переведено из существующей статьи в немецкой Википедии на [[: de: Karnaugh-Veitch-Diagramm]]; см. его историю для атрибуции. Вам также следует добавить шаблон {{Translated | de | Диаграмма Карно-Вейча}} к страница обсуждения. Для получения дополнительной информации см. Википедия: Перевод.

Пример карты Карно. На этом изображении фактически показаны две карты Карно: для функции ƒ, с помощью минтермы (цветные прямоугольники) и для его дополнения, используя maxterms (серые прямоугольники). На изображении, E() означает сумму минтермов, обозначенную в статье как ${displaystyle sum m_ {i}}$.

В Карта Карно (Км или K-карта) - метод упрощения Булева алгебра выражения. Морис Карно представил его в 1953 году^[1][2] как уточнение Эдвард В. Вейч 1952 год График Вейча,^[3][4] что на самом деле было переоткрытием Аллан Маркуанд 1881 год логическая диаграмма^[5] он же Диаграмма Маркуанда '^[4] но теперь основное внимание уделяется его полезности для коммутации цепей ».^[4] Поэтому диаграммы Вейча также известны как Диаграммы Маркуанда – Вейча,'^[4] и карты Карно как Карты Карно – Вейча (KV карты).

Карта Карно снижает потребность в обширных вычислениях за счет использования возможностей распознавания образов людьми.^[1] Это также позволяет быстро выявить и устранить потенциальные условия гонки.

Требуемые логические результаты переносятся из таблица истинности на двумерную сетку, где в картах Карно ячейки упорядочены в Код Грея,^[6][4] и каждая позиция ячейки представляет одну комбинацию входных условий, в то время как каждое значение ячейки представляет соответствующее выходное значение. Идентифицируются оптимальные группы единиц или нулей, которые представляют собой члены каноническая форма логики в исходной таблице истинности.^[7] Эти термины могут использоваться для написания минимального логического выражения, представляющего требуемую логику.

Карты Карно используются для упрощения требований реальной логики, чтобы их можно было реализовать с использованием минимального количества физических логических вентилей. А выражение суммы произведений всегда можно реализовать с помощью И ворота питаясь ИЛИ ворота, а выражение произведения сумм ведет к воротам ИЛИ, питающим ворота И.^[8] Карты Карно также можно использовать для упрощения логических выражений при разработке программного обеспечения. Логические условия, используемые, например, в условные утверждения, может быть очень сложным, что затрудняет чтение и сопровождение кода. После минимизации канонические выражения суммы произведений и произведений сумм могут быть реализованы напрямую с помощью логических операторов И и ИЛИ.^[9] Диаграммные и механические методы минимизации простых логических выражений существуют по крайней мере со времен средневековья. Более систематические методы минимизации сложных выражений начали разрабатываться в начале 1950-х годов, но до середины и конца 1980-х годов карта Карно была наиболее распространенной на практике.^[10]

пример

Карты Карно используются для упрощения Булева алгебра функции. Например, рассмотрим логическую функцию, описываемую следующим таблица истинности.

Таблица истинности функции

	А	B	C	D	${displaystyle f (A, B, C, D)}$
0	0	0	0	0	0
1	0	0	0	1	0
2	0	0	1	0	0
3	0	0	1	1	0
4	0	1	0	0	0
5	0	1	0	1	0
6	0	1	1	0	1
7	0	1	1	1	0
8	1	0	0	0	1
9	1	0	0	1	1
10	1	0	1	0	1
11	1	0	1	1	1
12	1	1	0	0	1
13	1	1	0	1	1
14	1	1	1	0	1
15	1	1	1	1	0

Ниже приведены две разные записи, описывающие одну и ту же функцию в неупрощенной булевой алгебре с использованием булевых переменных. А, B, C, D, и их обратные.

• ${displaystyle f (A, B, C, D) = sum _ {} m_ {i}, iin {6,8,9,10,11,12,13,14}}$ где ${displaystyle m_ {i}}$ являются минтермы для сопоставления (т. е. строк, которые имеют выход 1 в таблице истинности).
• ${displaystyle f (A, B, C, D) = prod _ {} M_ {i}, iin {0,1,2,3,4,5,7,15}}$ где ${displaystyle M_ {i}}$ являются maxterms для сопоставления (т. е. строк, которые имеют вывод 0 в таблице истинности).

Карта Карно

K-карта, нарисованная как на торе, так и на плоскости. Ячейки, отмеченные точками, находятся рядом.

Построение K-карты. Вместо выходных значений (крайние правые значения в таблице истинности) эта диаграмма показывает десятичное представление входных ABCD (крайние левые значения в таблице истинности), поэтому это не карта Карно.

В трех измерениях прямоугольник можно превратить в тор.

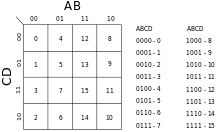
В приведенном выше примере четыре входные переменные могут быть объединены 16 различными способами, поэтому таблица истинности имеет 16 строк, а карта Карно - 16 позиций. Таким образом, карта Карно организована в виде сетки 4 × 4.

Индексы строк и столбцов (показанные сверху и снизу слева на карте Карно) упорядочены в Код Грея а не двоичный числовой порядок. Код Грея гарантирует, что между каждой парой соседних ячеек изменяется только одна переменная. Каждая ячейка завершенной карты Карно содержит двоичную цифру, представляющую выход функции для этой комбинации входов.

После того, как карта Карно построена, она используется для поиска одной из простейших возможных форм - каноническая форма - для информации в таблице истинности. Смежные единицы на карте Карно представляют возможности для упрощения выражения. Минтермы («минимальные термины») для окончательного выражения находятся обведением групп единиц на карте. Группы Minterm должны быть прямоугольными и иметь площадь, равную степени двойки (то есть 1, 2, 4, 8 ...). Прямоугольники Minterm должны быть как можно больше и не содержать нулей. Группы могут перекрываться, чтобы увеличивать каждую. Оптимальные группировки в приведенном ниже примере отмечены зеленой, красной и синей линиями, а красная и зеленая группы перекрываются. Красная группа - это квадрат 2 × 2, зеленая группа - это прямоугольник 4 × 1, а область перекрытия обозначена коричневым.

Ячейки часто обозначаются сокращением, которое описывает логическое значение входных данных, которые охватывает ячейка. Например, ОБЪЯВЛЕНИЕ будет означать ячейку, которая покрывает область 2x2, где А и D верны, т. е. ячейки под номерами 13, 9, 15, 11 на диаграмме выше. С другой стороны, АD будет означать ячейки, где А правда и D ложно (то есть D правда).

Сетка тороидально подключены, что означает, что прямоугольные группы могут перекрывать края (см. рисунок). Крайние правые ячейки на самом деле «смежны» с крайними левыми в том смысле, что соответствующие входные значения отличаются только на один бит; точно так же как и те, что на самом верху, и те, что внизу. Следовательно, АD может быть допустимым термином - он включает ячейки 12 и 8 вверху и переносится вниз, чтобы включать ячейки 10 и 14 - как есть BD, который включает четыре угла.

Решение

Диаграмма, показывающая две K-карты. K-карта для функции f (A, B, C, D) показана в виде цветных прямоугольников, которые соответствуют minterms. Коричневая область представляет собой перекрытие красного квадрата 2 × 2 и зеленого прямоугольника 4 × 1. K-карта для обратной функции f показана серыми прямоугольниками, которые соответствуют maxterms.

После того, как карта Карно построена и соседние единицы соединены прямоугольными и квадратными прямоугольниками, алгебраические термины могут быть найдены, исследуя, какие переменные остаются неизменными в каждом прямоугольнике.

Для красной группировки:

• А одинаков и равен 1 по всему блоку, поэтому его следует включить в алгебраическое представление красного минтерма.
• B не поддерживает одно и то же состояние (меняется с 1 на 0), поэтому его следует исключить.
• C не меняется. Он всегда равен 0, поэтому следует указать его дополнение NOT-C. Таким образом, C должны быть включены.
• D изменения, поэтому он исключен.

Таким образом, первый минтерм в булевом выражении суммы произведений равен АC.

Для зеленой группировки А и B поддерживать такое же состояние, пока C и D изменение. B равен 0 и должен быть инвертирован перед включением. Таким образом, второй член АB. Обратите внимание, что допустимо, чтобы зеленая группа перекрывалась с красной.

Таким же образом синяя группировка дает термин до н.эD.

Решения каждой группы объединены: нормальная форма схемы ${displaystyle A {overline {C}} + A {overline {B}} + BC {overline {D}}}$.

Таким образом, карта Карно послужила упрощением

${displaystyle {egin {align} f (A, B, C, D) = {} & {overline {A}} BC {overline {D}} + A {overline {B}}, {overline {C}}, {overline {D}} + A {overline {B}}, {overline {C}} D + A {overline {B}} C {overline {D}} + {} & A {overline {B}} CD + AB {overline {C}}, {overline {D}} + AB {overline {C}} D + ABC {overline {D}} = {} & A {overline {C}} + A {overline {B}} + BC {overline {D}} конец {выровнено}}}$

Это упрощение также можно было получить, тщательно применяя аксиомы булевой алгебры, но время, необходимое для этого, растет экспоненциально с увеличением количества членов.

Обратный

Обратное значение функции решается таким же образом путем группировки нулей.

Все три члена, описывающие обратное, показаны серыми прямоугольниками с разноцветными границами:

• коричневый: А, B
• золото: А, C
• синий: BCD

Это дает обратное:

${displaystyle {overline {f (A, B, C, D)}} = {overline {A}}, {overline {B}} + {overline {A}}, {overline {C}} + BCD}$

За счет использования Законы де Моргана, то произведение сумм можно определить:

${displaystyle {egin {выравнивается} f (A, B, C, D) & = {overline {overline {f (A, B, C, D)}}} & = {overline {{overline {A}}, {overline {B}} + {overline {A}}, {overline {C}} + BCD}} & = left ({overline {{overline {A}}, {overline {B}}}} ight) left) ({overline {{overline {A}}, {overline {C}}}} ight) left ({overline {BCD}} ight) & = left (A + Bight) left (A + Cight) left ({overline {B}} + {overline {C}} + {overline {D}} ight) конец {выровнено}}}$

Все равно

Значение ${displaystyle f (A, B, C, D)}$ для ABCD = 1111 заменяется на "все равно". Это полностью удаляет зеленый член и позволяет красному члену быть больше. Это также позволяет синему обратному члену сдвигаться и становиться больше

Карты Карно также позволяют упростить минимизацию функций, таблицы истинности которых включают "все равно «условия». Условие «безразлично» - это комбинация входных данных, для которых разработчик не заботится о том, что будет на выходе. Поэтому условия «безразлично» могут быть включены или исключены из любой прямоугольной группы в зависимости от того, что делает его больше. Обычно они обозначаются на карте знаком тире или X.

Пример справа такой же, как и в примере выше, но со значением ж(1,1,1,1) заменено на «все равно». Это позволяет красному члену полностью расширяться вниз и, таким образом, полностью удаляет зеленый член.

Это дает новое уравнение минимума:

${displaystyle f (A, B, C, D) = A + BC {overline {D}}}$

Обратите внимание, что первый член просто Ане АC. В этом случае элемент безразлично потерял термин (зеленый прямоугольник); упрощенный другой (красный); и удалил гоночную опасность (убрав желтый термин, как показано в следующем разделе о гоночных опасностях).

Обратный случай упрощается следующим образом:

${displaystyle {overline {f (A, B, C, D)}} = {overline {A}}, {overline {B}} + {overline {A}}, {overline {C}} + {overline {A }} D}$

Опасности гонки

Устранение

Карты Карно полезны для обнаружения и устранения условия гонки. Опасности гонки очень легко обнаружить с помощью карты Карно, потому что состояние гонки может существовать при перемещении между любой парой соседних, но не пересекающихся регионов, обозначенных на карте. Однако из-за природы кодирования Грея смежный имеет специальное определение, объясненное выше - мы фактически движемся по тору, а не по прямоугольнику, охватывая верх, низ и стороны.

• В примере над, потенциальное состояние гонки существует, когда C равно 1 и D равно 0, А равно 1, а B изменяется с 1 на 0 (переход из синего состояния в зеленое). Для этого случая определено, что выход остается неизменным на уровне 1, но поскольку этот переход не покрывается конкретным членом в уравнении, потенциал для Сбой (мгновенный переход выхода в 0) существует.
• В том же примере есть второй потенциальный сбой, который труднее обнаружить: когда D равно 0 и А и B оба равны 1, причем C изменяется с 1 на 0 (переход из синего состояния в красное). В этом случае сбой происходит от верхнего края карты к низу.

На этой диаграмме представлены гоночные опасности.

Выше диаграмма с согласованными условиями добавлена, чтобы избежать опасностей расы.

Возникнут ли на самом деле сбои, зависит от физической природы реализации, а нужно ли нам об этом беспокоиться, зависит от приложения. В тактовой логике достаточно, чтобы логика установила желаемое значение вовремя, чтобы уложиться в крайний срок. В нашем примере мы не рассматриваем синхронизированную логику.

В нашем случае дополнительный срок ${displaystyle A {overline {D}}}$ устранит потенциальную опасность гонки, установив мост между зеленым и синим выходными состояниями или синим и красным выходными состояниями: это показано как желтая область (которая оборачивается снизу вверх правой половины) на соседней диаграмме.

Срок избыточный с точки зрения статической логики системы, но такой избыточный, или согласованные условия, часто необходимы для обеспечения динамических характеристик без гонок.

Точно так же дополнительный срок ${displaystyle {overline {A}} D}$ должен быть добавлен к обратному, чтобы исключить другую потенциальную опасность гонки. Применение законов Де Моргана создает еще один продукт выражения сумм для ж, но с новым фактором ${displaystyle left (A + {overline {D}} ight)}$.

Примеры карт с двумя переменными

Ниже приведены все возможные карты Карно с 2-мя переменными и 2 × 2. Рядом с каждым из них перечислены минтермы в зависимости от ${displaystyle sum m ()}$ и гонка без опасностей (увидеть предыдущий раздел ) уравнение минимума. Минтерм определяется как выражение, которое дает наиболее минимальную форму выражения отображаемых переменных. Могут быть сформированы все возможные горизонтальные и вертикальные взаимосвязанные блоки. Эти блоки должны иметь размер степеней двойки (1, 2, 4, 8, 16, 32, ...). Эти выражения создают минимальное логическое отображение выражений минимальных логических переменных для отображаемых двоичных выражений. Вот все блоки с одним полем.

Блок может быть продолжен в нижней, верхней, левой или правой частях диаграммы. Это может даже выйти за пределы диаграммы для минимизации переменных. Это потому, что каждая логическая переменная соответствует каждому вертикальному столбцу и горизонтальной строке. Визуализацию k-карты можно считать цилиндрической. Поля по краям слева и справа смежны, а сверху и снизу - рядом. K-карты для четырех переменных должны быть изображены в виде бублика или тора. Четыре угла квадрата, нарисованного k-картой, смежны. Еще более сложные карты необходимы для 5 и более переменных.

• 

  Σм(0); K = 0

• 

  Σм(1); K = А′B′

• 

  Σм(2); K = AB′

• 

  Σм(3); K = А′B

• 

  Σм(4); K = AB

• 

  Σм(1,2); K = B′

• 

  Σм(1,3); K = А′

• 

  Σм(1,4); K = А′B′ + AB

• 

  Σм(2,3); K = AB′ + А′B

• 

  Σм(2,4); K = А

• 

  Σм(3,4); K = B

• 

  Σм(1,2,3); K = А ' + B′

• 

  Σм(1,2,4); K = А + B′

• 

  Σм(1,3,4); K = А′ + B

• 

  Σм(2,3,4); K = А + B

• 

  Σм(1,2,3,4); K = 1

Другие графические методы

Связанные методы графической минимизации включают:

• Диаграмма Маркуанда (1881) автор Аллан Маркуанд (1853–1924)^[5][4]
• График Вейча (1952) автор: Эдвард В. Вейч (1924–2013)^[3][4]

Смотрите также

• Алгебраическая нормальная форма (ANF)
• Диаграмма двоичного решения (BDD), структура данных, которая представляет собой сжатое представление логической функции.
• Минимизатор эвристической логики эспрессо
• Список тем по булевой алгебре
• Оптимизация логики
• Площадь Пеннета (аналогичная диаграмма в биологии)
• Алгоритм Куайна – Маккласки
• Разложение Рида – Мюллера
• Диаграмма Венна
• Полином Жегалкина

использованная литература

дальнейшее чтение

• Кац, Рэнди Ховард (1998) [1994]. Современный логический дизайн. Издательство Бенджамин / Каммингс. стр.70–85. Дои:10.1016/0026-2692(95)90052-7. ISBN  0-8053-2703-7.
• Вингрон, Шимон Питер (2004) [2003-11-05]. «Карты Карно». Теория переключения: понимание через логику предикатов. Берлин, Гейдельберг, Нью-Йорк: Springer-Verlag. С. 57–76. ISBN  3-540-40343-4.
• Викес, Уильям Э. (1968). «3.5. Диаграммы Вейча». Логический дизайн с интегральными схемами. Нью-Йорк, США: Джон Уайли и сыновья. стр.36–49. LCCN  68-21185. п. 36: […] Уточнение Диаграмма Венна в нем кружки заменены квадратами и расположены в виде матрицы. На диаграмме Вейтча квадраты помечены минтермы. Карно присвоил квадратам и их меткам единицы и нули и вывел общепринятую схему нумерации.
• Максфилд, Клайв «Макс» (29 ноября 2006 г.). «Логика Рида-Мюллера». Логика 101. EE Times. Часть 3. В архиве из оригинала на 2017-04-19. Получено 2017-04-19.
• Линд, Ларри Фредерик; Нельсон, Джон Кристофер Канлифф (1977). «Раздел 2.3». Анализ и дизайн последовательных цифровых систем. Macmillan Press. ISBN  0-33319266-4. (146 стр.)
• Держатель, Мишель Элизабет (март 2005 г.) [2005-02-14]. «Модифицированная техника карты Карно». IEEE Transactions по образованию. IEEE. 48 (1): 206–207. Дои:10.1109 / TE.2004.832879. eISSN  1557-9638. ISSN  0018-9359. S2CID  25576523. [2]
• Кавана, Джозеф (2008). Основы компьютерной арифметики и Verilog HDL (1-е изд.). CRC Press.
• Кохави, Цви; Джа, Нирадж К. (2009). Теория переключений и конечных автоматов (3-е изд.). Издательство Кембриджского университета. ISBN  978-0-521-85748-2.

внешние ссылки

• Обнаружение перекрывающихся прямоугольников, Герберт Гларнер.
• Использование карт Карно в практических приложениях, Схемотехнический проект управления светофором.
• K-Map Tutorial для 2, 3, 4 и 5 переменных
• Пример карты Карно
• УПРОЩЕНИЕ БУЛЕВЫХ ФУНКЦИЙ POCKET – PC, Ledion Bitincka - George E. Antoniou
• Устранение неполадок K-Map