В динамика жидкостей, Джет Ландау – Сквайра или же Затопленная струя Ландау описывает круглую затопленную струю, исходящую из точечного источника импульса в бесконечную жидкую среду того же типа. Это точное решение уравнений Навье-Стокса, которое было впервые обнаружено Лев Ландау в 1944 г.[1][2] а позже Герберт Сквайр в 1951 г.[3] Фактически, автомодельное уравнение было впервые выведено Н. А. Слезкиным в 1934 г.[4] но никогда не относился к струе. Следуя работам Ландау, В. И. Яцеев в 1950 г. получил общее решение уравнения.[5]
Математическое описание

Линии тока струи Ландау-Сквайра при c = 0,01

Линии тока струи Ландау-Сквайра при c = 0,1
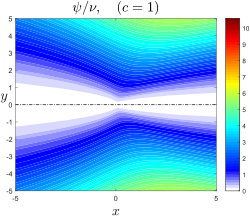
Линии тока струи Ландау-Сквайра при c = 1
Проблема описана в сферические координаты  с компонентами скорости
с компонентами скорости  . Течение осесимметрично, т.е. не зависит от
. Течение осесимметрично, т.е. не зависит от  . Тогда уравнение неразрывности и несжимаемая Уравнения Навье – Стокса сократить до
. Тогда уравнение неразрывности и несжимаемая Уравнения Навье – Стокса сократить до
![{ displaystyle { begin {align} & { frac {1} {r ^ {2}}} { frac { partial} { partial r}} (r ^ {2} u) + { frac { 1} {r sin theta}} { frac { partial} { partial theta}} (v sin theta) = 0 [8pt] & u { frac { partial u} { partial r}} + { frac {v} {r}} { frac { partial u} { partial theta}} - { frac {v ^ {2}} {r}} = - { frac { 1} { rho}} { frac { partial p} { partial r}} + nu left ( nabla ^ {2} u - { frac {2u} {r ^ {2}}} - { frac {2} {r ^ {2}}} { frac { partial v} { partial theta}} - { frac {2v cot theta} {r ^ {2}}} right ) [8pt] & u { frac { partial v} { partial r}} + { frac {v} {r}} { frac { partial v} { partial theta}} + { frac {uv} {r}} = - { frac {1} { rho r}} { frac { partial p} { partial theta}} + nu left ( nabla ^ {2} v + { frac {2} {r ^ {2}}} { frac { partial u} { partial theta}} - { frac {v} {r ^ {2} sin ^ {2} theta }} right) end {выровнен}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/29a48d8946a90c045c65908f76e200c62a56723b)
куда

Для решения доступно автомодельное описание в следующем виде:[6]

Подставляя указанную выше автомодельную форму в основные уравнения и используя граничные условия  на бесконечности давление находится в виде
на бесконечности давление находится в виде

куда  является константой. Используя это давление, снова находим из уравнения импульса:
является константой. Используя это давление, снова находим из уравнения импульса:
![{ displaystyle - { frac {u ^ {2}} {r}} + { frac {v} {r}} { frac { partial u} { partial theta}} = { frac { nu} {r ^ {2}}} left [2u + { frac {1} { sin theta}} { frac { partial} { partial theta}} left ( sin theta { frac { partial u} { partial theta}} right) right] + { frac {2c_ {1}} {r ^ {3}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d9956ba9728a61e68fb8213cfb695f88763e84d)
Замена  к
к  как независимая переменная, скорости становятся
как независимая переменная, скорости становятся

(для краткости используется тот же символ для  и
и  хотя функционально они одинаковы, но принимают разные числовые значения), и уравнение становится
хотя функционально они одинаковы, но принимают разные числовые значения), и уравнение становится
![{ displaystyle f '^ {2} + ff' '= 2f' + [(1- mu ^ {2}) f ''] '- 2c_ {1}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79f354361cfd11a18193a9fff5fe79599aa2c200)
После двух интегрирований уравнение сводится к

куда  и
и  - константы интегрирования. Вышеприведенное уравнение представляет собой Уравнение Риккати. После некоторых вычислений можно показать, что общее решение имеет вид
- константы интегрирования. Вышеприведенное уравнение представляет собой Уравнение Риккати. После некоторых вычислений можно показать, что общее решение имеет вид
![{ Displaystyle е = альфа (1+ му) + бета (1- му) + { гидроразрыва {2 (1- му ^ {2}) (1+ му) ^ { бета}} {(1- mu) ^ { alpha}}} left [c- int _ {1} ^ { mu} { frac {(1+ mu) ^ { beta}} {(1- mu) ^ { alpha}}} right] ^ {- 1},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/798d91fc7d69ce97747504b635e984b2afdc3708)
куда  являются константами. Физически релевантное решение струи соответствует случаю
являются константами. Физически релевантное решение струи соответствует случаю  (Эквивалентно мы говорим, что
(Эквивалентно мы говорим, что  , так что решение не имеет особенностей на оси симметрии, кроме начала координат).[7] Следовательно,
, так что решение не имеет особенностей на оси симметрии, кроме начала координат).[7] Следовательно,

Функция  относится к функция потока в качестве
относится к функция потока в качестве  , таким образом, контуры
, таким образом, контуры  для разных значений
для разных значений  обеспечивает оптимизацию. Постоянная
обеспечивает оптимизацию. Постоянная  описывает силу в начале координат, действующую в направлении струи (эта сила равна скорости передачи импульса через любую сферу вокруг начала координат плюс силу в направлении струи, прилагаемую сферой из-за давления и сил вязкости), точное соотношение между силой и константой дается выражением
описывает силу в начале координат, действующую в направлении струи (эта сила равна скорости передачи импульса через любую сферу вокруг начала координат плюс силу в направлении струи, прилагаемую сферой из-за давления и сил вязкости), точное соотношение между силой и константой дается выражением

Решение описывает струю жидкости, быстро удаляющуюся от источника и увлекающую медленно движущуюся жидкость за пределы струи. Край струи можно определить как место, где линии тока находятся на минимальном расстоянии от оси, т. Е. Край определяется как

Следовательно, сила может быть выражена альтернативно, используя этот полуугол конической границы струи:

Когда сила становится большой, полуугол струи становится малым, и в этом случае

и раствор внутри и снаружи струи становится

Струя в этом предельном случае называется Струя Schlichting. С другой стороны, когда сила мала,

полуугол приближается к 90 градусам (нет внутренней и внешней области, вся область рассматривается как одна область), само решение идет к

Смотрите также
Рекомендации
- ^ Ландау, Л. Д. (1944). Новое точное решение уравнений Навье-Стокса. В Докладах Академии Наук СССР (т. 44, с. 311-314).
- ^ Тер Хаар, Дирк, изд. Сборник статей Л. Д. Ландау. Эльзевир, 2013.
- ^ Сквайр, Х. Б. (1951). Круглая ламинарная струя. Ежеквартальный журнал механики и прикладной математики, 4(3), 321-329.
- ^ Слезкин Н. А. "О точном решении уравнений вязкого течения, Уч. Зап." (1934): 89-90.
- ^ Яцеев, В. И. (1950). Об одном классе точных решений уравнений движения вязкой жидкости. Журнал технической физики, 20 (11), 1031-1034.
- ^ Седов, Л. И. (1993). Методы подобия и размерности в механике. CRC Press.
- ^ Бэтчелор, Г. К. (2000). Введение в гидродинамику. Пресса Кембриджского университета.







![{ displaystyle { begin {align} & { frac {1} {r ^ {2}}} { frac { partial} { partial r}} (r ^ {2} u) + { frac { 1} {r sin theta}} { frac { partial} { partial theta}} (v sin theta) = 0 [8pt] & u { frac { partial u} { partial r}} + { frac {v} {r}} { frac { partial u} { partial theta}} - { frac {v ^ {2}} {r}} = - { frac { 1} { rho}} { frac { partial p} { partial r}} + nu left ( nabla ^ {2} u - { frac {2u} {r ^ {2}}} - { frac {2} {r ^ {2}}} { frac { partial v} { partial theta}} - { frac {2v cot theta} {r ^ {2}}} right ) [8pt] & u { frac { partial v} { partial r}} + { frac {v} {r}} { frac { partial v} { partial theta}} + { frac {uv} {r}} = - { frac {1} { rho r}} { frac { partial p} { partial theta}} + nu left ( nabla ^ {2} v + { frac {2} {r ^ {2}}} { frac { partial u} { partial theta}} - { frac {v} {r ^ {2} sin ^ {2} theta }} right) end {выровнен}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/29a48d8946a90c045c65908f76e200c62a56723b)





![{ displaystyle - { frac {u ^ {2}} {r}} + { frac {v} {r}} { frac { partial u} { partial theta}} = { frac { nu} {r ^ {2}}} left [2u + { frac {1} { sin theta}} { frac { partial} { partial theta}} left ( sin theta { frac { partial u} { partial theta}} right) right] + { frac {2c_ {1}} {r ^ {3}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d9956ba9728a61e68fb8213cfb695f88763e84d)





![{ displaystyle f '^ {2} + ff' '= 2f' + [(1- mu ^ {2}) f ''] '- 2c_ {1}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79f354361cfd11a18193a9fff5fe79599aa2c200)



![{ Displaystyle е = альфа (1+ му) + бета (1- му) + { гидроразрыва {2 (1- му ^ {2}) (1+ му) ^ { бета}} {(1- mu) ^ { alpha}}} left [c- int _ {1} ^ { mu} { frac {(1+ mu) ^ { beta}} {(1- mu) ^ { alpha}}} right] ^ {- 1},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/798d91fc7d69ce97747504b635e984b2afdc3708)













