Список секундных моментов площади - List of second moments of area
Ниже приводится список секундных моментов площади некоторых форм. В второй момент площади, также известный как момент инерции области, является геометрическим свойством области, которое отражает то, как ее точки распределены относительно произвольной оси. В единица измерения размерности второго момента площади - это длина в четвертой степени, L4, и его не следует путать с момент инерции массы. Однако, если деталь тонкая, момент инерции массы равен удельной площади, умноженной на момент инерции площади.
Вторые моменты площади
Учтите, что в следующих уравнениях:
и
.
| Описание | Фигура | Момент инерции площади | Комментарий |
|---|---|---|---|
| Закрашенная круглая область радиуса р |  | [1] | это Полярный момент инерции. |
| An кольцо внутреннего радиуса р1 и внешний радиус р2 |  | Для тонких трубок и . Итак, для тонкой трубки . это Полярный момент инерции. | |
| Заполненный круговой сектор угла θ в радианы и радиус р относительно оси, проходящей через центр тяжести сектора и центр круга |  | Эта формула верна только для 0 ≤ ≤ | |
| Закрашенный полукруг с радиусом р относительно горизонтальной линии, проходящей через центр тяжести площади |  | [2] | |
| Закрашенный полукруг, как указано выше, но относительно оси, коллинеарной с основанием | 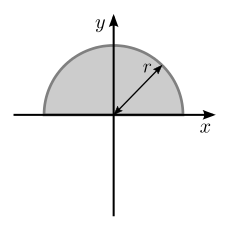 | [2] | : Это следствие теорема о параллельной оси и тот факт, что расстояние между осями x предыдущей и этой оси равно |
| Закрашенная четверть круга с радиусом р с осями, проходящими через базы |  | [3] | |
| Закрашенная четверть круга с радиусом р с осями, проходящими через центроид |  | [3] | Это следствие теорема о параллельной оси и тот факт, что расстояние между этими двумя осями равно |
| Заполненный эллипс радиус которого по Иксось а и радиус которого по уось б |  | ||
| Закрашенная прямоугольная область с шириной основания б и высота час | 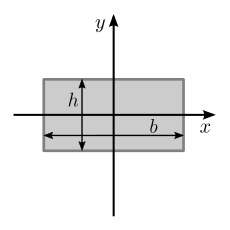 | [4] | |
| Закрашенная прямоугольная область, как указано выше, но относительно оси, коллинеарной с основанием |  | [4] | Это результат теорема о параллельной оси |
| Дупло прямоугольник с внутренним прямоугольником шириной б1 и чей рост час1 |  | ||
| Заполненная треугольная область с шириной основания б, высота час и смещение верхней вершины аотносительно оси, проходящей через центроид |  | [5] | |
| Заливанная треугольная область, как указано выше, но относительно оси, коллинеарной с основанием |  | [5] | Это следствие теорема о параллельной оси |
| Угол с равными ножками, обычно используемый в инженерных приложениях |  | это часто неиспользуемое произведение инерции, используемое для определения инерции с вращающейся осью | |
| Заполненный правильный шестиугольник с длиной стороны а |  | Результат действителен как для горизонтальной, так и для вертикальной оси, проходящей через центроид, и, следовательно, также действителен для оси с произвольным направлением, проходящей через начало координат. |
Теорема о параллельной оси

Теорема о параллельных осях может использоваться для определения второго момента площади твердого тела вокруг любой оси, учитывая момент инерции тела относительно параллельной оси, проходящей через центр масс объекта, и расстояние по перпендикуляру (d) между осями.
Смотрите также
Рекомендации
- ^ "Круг". eFunda. Получено 2006-12-30.
- ^ а б "Круговая половина". eFunda. Получено 2006-12-30.
- ^ а б «Четверть круга». eFunda. Получено 2006-12-30.
- ^ а б «Прямоугольная площадка». eFunda. Получено 2006-12-30.
- ^ а б «Треугольная зона». eFunda. Получено 2006-12-30.











































