Девять лемм - Nine lemma

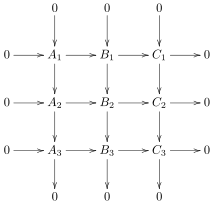
Девять lemma.svg

В математика, то девять лемм (или лемма 3 × 3) - утверждение о коммутативные диаграммы и точные последовательности действительно в категории группы и любой абелева категория. В нем говорится: если диаграмма справа является коммутативной диаграммой и все столбцы, а также две нижние строки точны, то верхняя строка также точна. Аналогичным образом, если все столбцы, а также две верхние строки точны, то нижняя строка также точна. Точно так же, поскольку диаграмма симметрична относительно своей диагонали, строки и столбцы также могут меняться местами в приведенном выше.

Лемму о девяти можно доказать прямым погоня за диаграммой, или применяя лемма о змеях (в два нижних ряда в первом случае и в два верхних ряда во втором).

Линдерхольм (стр. 201) предлагает сатирический взгляд на лемму девяти:

"Нарисовать крестики-нолики доска ... Не заполняйте ее крестиками и ноликами ... Вместо этого используйте изогнутые стрелки ... Помашите руками над этой доской сложными узорами. Сделайте несколько нулей, но не в квадратах; поместите их на обоих концах горизонтальной и вертикальной линий. Делать лица. Теперь вы доказали:
(а) Девять лемм
(б) Лемма Шестнадцати
(c) Лемма Двадцати пяти ... "

Есть два варианта леммы девять: точная лемма девять и симметричная девятка (см. Леммы 3.3, 3.4 в главе XII книги [1]).

Рекомендации

  1. ^ Маклейн, Сондерс (1967). Гомология (Repr. Of 1. ed. 1963. ed.). Берлин [u.a.]: Springer. С. 365–366. ISBN  9783540586623.