Коммутативная диаграмма - Википедия - Commutative diagram

Коммутативная диаграмма, использованная при доказательстве пять лемм.

В математика, и особенно в теория категорий, а коммутативная диаграмма это диаграмма так, что все направленные пути на диаграмме с одинаковыми начальной и конечной точками приводят к одному и тому же результату.^[1] Говорят, что коммутативные диаграммы играют роль в теории категорий: уравнения играть в алгебра (видеть Барр и Уэллс (2002), Раздел 1.7)).

Описание

Коммутативная диаграмма часто состоит из трех частей:

объекты (также известен как вершины)
морфизмы (также известен как стрелки или же края)
дорожки или композиты

Символы стрелок

В текстах по алгебре тип морфизма может обозначаться разными стрелками:

А мономорфизм (инъективный гомоморфизм) можно пометить ${ displaystyle hookrightarrow}$ .^[2]
An эпиморфизм (сюръективный гомоморфизм) может быть помечен ${ displaystyle twoheadrightarrow}$ .
An изоморфизм (биективный гомоморфизм) можно пометить ${ Displaystyle { overset { sim} { rightarrow}}}$ .
Пунктирная стрелка обычно представляет утверждение о том, что указанный морфизм существует (если остальная часть диаграммы верна); стрелка может быть дополнительно помечена как ${ Displaystyle существует}$ $существуют$ .
- Если морфизм к тому же уникален, то пунктирная стрелка может быть помечена ${ displaystyle!}$ или же ${ displaystyle существует!}$ .

Проверка коммутативности

Коммутативность имеет смысл для многоугольник любого конечного числа сторон (включая только 1 или 2), и диаграмма коммутативна, если каждая многоугольная поддиаграмма коммутативна.

Обратите внимание, что диаграмма может быть некоммутативной, т. Е. Композиция разных путей на диаграмме может не давать одинаковый результат.

Фразы

Такие фразы, как «эта коммутативная диаграмма» или «диаграмма коммутирует»^[2] может быть использовано.

Примеры

На левой диаграмме, которая выражает первая теорема об изоморфизме коммутативность треугольника означает, что ${ displaystyle f = { тильда {f}} circ pi}$ . На правой диаграмме коммутативность квадрата означает ${ Displaystyle ч сирк е = к сирк г}$ .

Чтобы диаграмма, приведенная ниже, коммутировала, должны быть выполнены три равенства:

${ Displaystyle г CIRC H CIRC G = H CIRC G CIRC L}$
${ Displaystyle м circ g = G circ l}$
${ displaystyle r circ h = H circ m}$

Здесь, поскольку первое равенство следует из двух последних, достаточно показать, что (2) и (3) верны, чтобы диаграмма коммутировала. Однако, поскольку равенство (3) обычно не следует из двух других, обычно недостаточно иметь только равенства (1) и (2), если нужно показать, что диаграмма коммутирует.

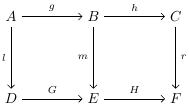Схема погони

Схема погони (также называемый схематический поиск) - метод математическое доказательство используется особенно в гомологическая алгебра, где свойство некоторого морфизма устанавливается путем отслеживания элементов коммутативной диаграммы.^[3] Доказательство путем поиска диаграммы обычно включает формальное использование свойств диаграммы, таких как инъективный или же сюръективный карты или точные последовательности.^[4] А силлогизм построен, для которого графическое отображение диаграммы является просто наглядным пособием. Отсюда следует, что в конце концов нужно «гоняться» за элементами на диаграмме, пока не будет построен или проверен желаемый элемент или результат.

Примеры доказательств по диаграммам включают те, которые обычно приводятся для пять лемм, то лемма о змеях, то лемма о зигзаге, а девять лемм.

В теории высших категорий

В теории высших категорий рассматриваются не только объекты и стрелки, но и стрелки между стрелками, стрелки между стрелками между стрелками и т. Д. до бесконечности. Например, категория малых категорий Кот естественно 2-категория, с функторы как его стрелки и естественные преобразования как стрелки между функторами. В этой настройке коммутативные диаграммы также могут включать в себя эти более высокие стрелки, которые часто изображаются в следующем стиле: ${ displaystyle Rightarrow}$ . Например, следующая (несколько тривиальная) диаграмма изображает две категории C и Dвместе с двумя функторами F, грамм : C → D и естественное преобразование α : F ⇒ грамм:

Есть два вида композиций в 2 категории (называемые вертикальная композиция и горизонтальная композиция), а также могут быть изображены через вставка диаграмм (видеть 2-категория # Определение Например).

Диаграммы как функторы

Коммутативная диаграмма в категории C можно интерпретировать как функтор из индексной категории J к C; называют функтор a диаграмма.

Более формально коммутативная диаграмма - это визуализация диаграммы, индексированной категория poset. Такая диаграмма обычно включает:

узел для каждого объекта в категории индекса,
стрелка для порождающего набора морфизмов (исключая тождественные карты и морфизмы, которые могут быть выражены как композиции),
коммутативность диаграммы (равенство различных составов карт между двумя объектами), соответствующая уникальности карты между двумя объектами в категории poset.

И наоборот, учитывая коммутативную диаграмму, она определяет категорию poset, где:

объекты - это узлы,
существует морфизм между любыми двумя объектами тогда и только тогда, когда между узлами существует (направленный) путь,
с тем отношением, что этот морфизм уникален (любая композиция отображений определяется своей областью и целью: это аксиома коммутативности).

Однако не всякая диаграмма коммутирует (понятие диаграммы строго обобщает коммутативную диаграмму). В качестве простого примера диаграмма одного объекта с эндоморфизмом ( ${ displaystyle f двоеточие от X до X}$ ) или двумя параллельными стрелками ( ${ displaystyle bullet rightrightarrows bullet}$ , то есть, ${ displaystyle f, g двоеточие от X до Y}$ , иногда называемый бесплатный колчан ), как используется в определении эквалайзер не нужно добираться. Кроме того, диаграммы могут быть беспорядочными или невозможными для рисования, когда количество объектов или морфизмов велико (или даже бесконечно).

Смотрите также

Математическая диаграмма

Библиография

Адамек, Иржи; Хорст Херрлих; Джордж Э. Стрекер (1990), Абстрактные и конкретные категории (PDF), Джон Уайли и сыновья, ISBN 0-471-60922-6 Теперь доступна бесплатная онлайн-версия (4,2 МБ в формате PDF).
Барр, Майкл; Уэллс, Чарльз (2002), Топосы, тройки и теории (PDF), ISBN 0-387-96115-1 Доработанная и исправленная бесплатная онлайн-версия Grundlehren der Mathematischen Wissenschaften (278) Springer-Verlag, 1983).

внешняя ссылка

Диаграмма Погоня в MathWorld
WildCats пакет теории категорий для Mathematica. Манипуляция и визуализация объектов, морфизмы, категории, функторы, естественные преобразования.

[1] Вайсштейн, Эрик В. «Коммутативная диаграмма». mathworld.wolfram.com. Получено 2019-11-25.

[:0-2] а ^б «Математика - Теория категорий - Стрелка - Мартин Бейкер». www.euclideanspace.com. Получено 2019-11-25.

[3] «Окончательный глоссарий высшего математического жаргона - погоня». Математическое хранилище. 2019-08-01. Получено 2019-11-25.

[4] Вайсштейн, Эрик В. "Погоня за диаграммой". mathworld.wolfram.com. Получено 2019-11-25.

[1]

[2]

[3]

[4]