Ядро (теория категорий) - Kernel (category theory)
Эта статья нужны дополнительные цитаты для проверка. (Декабрь 2009 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |
В теория категорий и его приложения к другим отраслям математика, ядра являются обобщением ядер групповые гомоморфизмы, ядра модульные гомоморфизмы и некоторые другие ядра из алгебры. Интуитивно понятно, что ядро морфизм ж : Икс → Y это «самый общий» морфизм k : K → Икс который дает ноль при составлении с (сопровождаемым) ж.
Обратите внимание, что пары ядер и различия ядер (также известный как двоичный эквалайзеры ) иногда называют "ядро"; хотя и связаны, это не совсем одно и то же и в этой статье не обсуждается.
Определение
Позволять C быть категория.Чтобы определить ядро в общем теоретико-категориальном смысле, C необходимо иметь нулевые морфизмы.В этом случае, если ж : Икс → Y произвольный морфизм в C, то ядро ж является эквалайзер из ж и нулевой морфизм из Икс к YВ символах:
- кер (ж) = экв (ж, 0XY)
Чтобы быть более точным, следующие универсальная собственность может быть использован. Ядро ж является объект K вместе с морфизмом k : K → Икс такой, что:
- ж ∘k нулевой морфизм из K к Y;
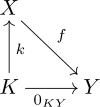
- Учитывая любой морфизм k′ : K′ → Икс такой, что ж ∘k′ - нулевой морфизм, существует единственный морфизм ты : K′ → K такой, что k∘ты = k ′.

Обратите внимание, что во многих конкретный контекстах, можно было бы ссылаться на объект K как "ядро", а не морфизм k.В таких ситуациях K будет подмножество из Икс, и этого было бы достаточно, чтобы восстановить k как карта включения; в неконкретном случае, напротив, нам понадобится морфизм k описать как K следует интерпретировать как подобъект из Икс. В любом случае можно показать, что k всегда мономорфизм (в категорическом смысле). Можно представить ядро как пару (K, k), а не просто K или же k один.
Не каждому морфизму требуется ядро, но если оно есть, то все его ядра изоморфны в сильном смысле: если k : K → Икс и ℓ : L → Икс ядра ж : Икс → Y, то существует единственный изоморфизм φ: K → L такой, что ℓ∘φ = k.
Примеры
Ядра знакомы по многим категориям из абстрактная алгебра, например, категория группы или категория (слева) модули за фиксированный звенеть (включая векторные пространства за фиксированный поле ). Чтобы быть точным, если ж : Икс → Y это гомоморфизм в одной из этих категорий, и K это его ядро в обычном алгебраическом смысле, тогда K это подалгебра из Икс и гомоморфизм включения из K к Икс является ядром в категорическом смысле.
Обратите внимание, что в категории моноиды теоретико-категориальные ядра существуют так же, как и для групп, но эти ядра не несут достаточной информации для алгебраических целей. Поэтому понятие ядра, изучаемое в теории моноидов, немного отличается (см. # Отношение к алгебраическим ядрам ниже).
в категория унитальных колец, в теоретико-категориальном смысле ядер нет; действительно, в этой категории нет даже нулевых морфизмов. Тем не менее в теории колец все еще изучается понятие ядра, которое соответствует ядрам в категория неунитальных колец.
В категории точечные топологические пространства, если ж : Икс → Y - непрерывное точечное отображение, то прообраз отмеченной точки, K, является подпространством Икс. Карта включения K в Икс категоричное ядро ж.
Отношение к другим категориальным понятиям
Двойственная концепция ядра - это концепция коядро То есть ядро морфизма - его коядро в противоположная категория, наоборот.
Как упоминалось выше, ядро - это тип двоичного эквалайзера, или разностное ядро И наоборот, в предаддитивная категория, каждый бинарный эквалайзер может быть построен как ядро, а именно: эквалайзер морфизмов ж и грамм ядро разница грамм − жВ символах:
- экв (ж, грамм) = ker (грамм − ж).
Именно из-за этого бинарные эквалайзеры называются «разностными ядрами» даже в непредаддитивных категориях, где морфизмы не могут быть вычтены.
Каждое ядро, как и любой другой эквалайзер, является мономорфизм Наоборот, мономорфизм называется нормальный если это ядро морфизма. Категория называется нормальный если каждый мономорфизм нормален.
Абелевы категории, в частности, всегда нормальны. В этой ситуации ядро коядро любого морфизма (который всегда существует в абелевой категории) оказывается изображение этого морфизма; в символах:
- я ж = ker coker ж (в абелевой категории)
Когда м это мономорфизм, это должен быть собственный образ; таким образом, абелевы категории не только нормальны, так что каждый мономорфизм является ядром, но мы также знаем который морфизм мономорфизм является ядром, а именно его коядром.
- м = ker (коксователь м) (для мономорфизмов в абелевой категории)
Связь с алгебраическими ядрами
Универсальная алгебра определяет понятие ядра для гомоморфизмов между двумя алгебраические структуры того же вида. Эта концепция ядра измеряет, насколько данный гомоморфизм далек от инъективный Между этим алгебраическим понятием и категоричным понятием ядра есть некоторое совпадение, поскольку оба они обобщают ситуацию с группами и модулями, упомянутыми выше. В целом, однако, универсально-алгебраическое понятие ядра больше похоже на теоретико-категориальное понятие ядра. пара ядер В частности, пары ядер могут использоваться для интерпретации ядер в теории моноидов или теории колец в терминах теории категорий.
Источники
- Awodey, Стив (2010) [2006]. Теория категорий (PDF). Oxford Logic Guides. 49 (2-е изд.). Издательство Оксфордского университета. ISBN 978-0-19-923718-0.
- Ядро в nLab
