Категория запятых - Comma category
Эта статья включает в себя список общих Рекомендации, но он остается в основном непроверенным, потому что ему не хватает соответствующих встроенные цитаты. (Март 2016 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |
В математика, а категория запятой (особый случай - категория срезов) является конструкцией в теория категорий. Это дает другой способ взглянуть на морфизмы: вместо того, чтобы просто связывать объекты категория друг для друга морфизмы становятся самостоятельными объектами. Это понятие было введено в 1963 г. Ф. В. Лавер (Лавер, 1963, стр. 36), хотя техника не[нужна цитата ] стали широко известны много лет спустя. Некоторые математические концепции можно рассматривать как категории с запятыми. Категории запятых также гарантируют существование некоторых пределы и копределы. Название происходит от обозначения, первоначально использовавшегося Ловером, в котором участвовали запятая знак препинания. Название сохраняется, даже несмотря на то, что стандартные обозначения были изменены, поскольку использование запятой в качестве оператора потенциально сбивает с толку, и даже Ловеру не нравится малоинформативный термин «категория запятой» (Lawvere, 1963, стр. 13).
Определение
Самая общая конструкция категорий запятых включает два функторы с таким же кодоменом. Часто один из них будет иметь домен 1 (категория одного объекта и одного морфизма). В некоторых статьях теории категорий рассматриваются только эти частные случаи, но термин «запятая категория» на самом деле гораздо более общий.
Общая форма
Предположим, что , , и категории, и и (для источника и цели) являются функторы:
Мы можем сформировать категорию запятой следующее:
- Объекты все тройки с объект в , объект в , и морфизм в .
- Морфизмы из к все пары куда и морфизмы в и соответственно, так что следующая диаграмма ездит на работу:
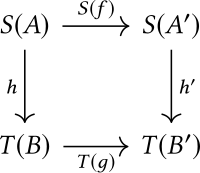
Морфизмы составляются взятием быть , если последнее выражение определено. Морфизм идентичности на объекте является .
Категория среза
Первый частный случай возникает, когда , функтор это функтор идентичности, и (категория с одним объектом и один морфизм). потом для какого-то объекта в .
В этом случае записывается категория запятой , и его часто называют категория срезов над или категория объекты над . Объекты можно упростить до пар , куда . Иногда, обозначается . Морфизм из к в категории срезов можно упростить до стрелки сделать следующую диаграмму коммутируемой:
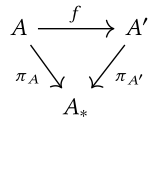
Категория Coslice
В двойной понятие категории среза - это категория среза. Здесь, , есть домен и является функтором тождества.
В этом случае часто пишется категория запятой , куда является объектом выбран . Это называется категория coslice относительно , или категория объекты под . Объекты парные с . Данный и , морфизм в категории кослиц - это отображение сделать следующую диаграмму коммутируемой:
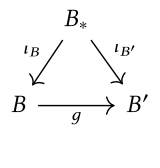
Категория стрелки
и находятся функторы идентичности на (так ).
В данном случае категория запятой - это категория стрелки. . Его объекты - морфизмы , а его морфизмы - коммутирующие квадраты в .[1]

Другие варианты
В случае категории среза или среза тождественный функтор может быть заменен каким-либо другим функтором; это дает семейство категорий, особенно полезных при изучении присоединенные функторы. Например, если это забывчивый функтор отображение абелева группа к его базовый набор, и некоторые фиксированные набор (рассматривается как функтор от 1), то категория запятой есть объекты, которые являются картами из к набору, лежащему в основе группы. Это относится к левому сопряженному , который является функтором, отображающим множество в свободная абелева группа имея это в качестве основы. В частности, исходный объект из каноническая инъекция , куда свободная группа, порожденная .
Объект называется морфизм из к или -структурированная стрелка с доменом .[1] Объект называется морфизм из к или -конструктурированная стрелка с кодоменом .[1]
Другой особый случай возникает, когда оба и являются функторами с областью . Если и , то категория запятой , написано , это дискретная категория чьи объекты являются морфизмами из к .
An категория установщика является (неполной) подкатегорией категории запятой, где и необходимы. Категория "запятая" также может использоваться для вставки и , куда и являются двумя проекционными функторами из Категория продукта .
Характеристики
Для каждой категории запятой есть забывчивые функторы от нее.
- Функтор домена, , который отображает:
- объекты: ;
- морфизмы: ;
- Функтор кодомена, , который отображает:
- объекты: ;
- морфизмы: .
- Функтор стрелки, , который отображает:
- объекты: ;
- морфизмы: ;
Примеры использования
Некоторые известные категории
Несколько интересных категорий имеют естественное определение в терминах категорий запятых.
- Категория заостренные наборы категория запятая, с быть (выбирающим функтором) любым одноэлементный набор, и (тождественный функтор) категория наборов. Каждый объект этой категории представляет собой набор вместе с функцией, выбирающей какой-либо элемент набора: «базовую точку». Морфизмы - это функции на множествах, которые отображают базовые точки в базовые точки. Аналогичным образом можно сформировать категорию заостренные места .
- Категория ассоциативных алгебр над кольцом категория coslice , поскольку любой гомоморфизм колец вызывает ассоциативный -алгебра на , наоборот. Морфизмы тогда карты которые заставляют диаграмму коммутировать.
- Категория графики является , с функтор, принимающий набор к . Объекты тогда состоят из двух наборов и функции; это индексирующий набор, набор узлов, а выбирает пары элементов для каждого входа из . То есть, выбирает определенные края из набора возможных краев. Морфизм в этой категории состоит из двух функций, одна из которых относится к набору индексации, а другая - к набору узлов. Они должны «согласиться» в соответствии с общим определением, приведенным выше, что означает, что должен удовлетворить . Другими словами, край, соответствующий определенному элементу набора индексирования, при преобразовании должен быть таким же, как край для переведенного индекса.
- Многие операции «расширения» или «маркировки» могут быть выражены в терминах категорий, запятых. Позволять - функтор, переводящий каждый граф в набор его ребер, и пусть быть (выбирающим функтором) определенным множеством: тогда - категория графов, ребра которых помечены элементами из . Такую форму категории запятых часто называют объекты -над - тесно связан с «объектами над "обсуждалось выше. Здесь каждый объект принимает форму , куда это граф и функция из краев к . Узлы графа могут быть помечены практически таким же образом.
- Категория называется местно декартово закрыто если каждый кусочек декартово закрыто (см. выше понятие ломтик). Локально декартовы закрытые категории - это классификация категорий из теории зависимых типов.
Пределы и универсальные морфизмы
Пределы и копределы в категориях запятые могут быть «унаследованы». Если и находятся полный, это непрерывный функтор, и - еще один функтор (не обязательно непрерывный), то категория запятой произведено завершено,[2] и проекционные функторы и непрерывны. Аналогично, если и неполные, и является непрерывный, тогда коколонна, а проекционные функторы коконепрерывны.
Например, обратите внимание, что в приведенной выше конструкции категории графов как категории запятых категория множеств полна и коколонна, а тождественный функтор непрерывен и коконепрерывен. Таким образом, категория графов полна и коколонна.
Понятие о универсальный морфизм к определенному копилку или от предела может быть выражено через категорию запятой. По сути, мы создаем категорию, объектами которой являются конусы, а ограничивающим конусом - конус. конечный объект; тогда каждый универсальный морфизм для предела - это просто морфизм конечного объекта. Это работает в двойном случае, когда категория коконов имеет исходный объект. Например, пусть быть категорией с функтор, принимающий каждый объект к и каждая стрелка к . Универсальный морфизм из к состоит по определению из объекта и морфизм с универсальным свойством, что для любого морфизма есть уникальный морфизм с . Другими словами, это объект из категории запятой. наличие морфизма к любому другому объекту в этой категории; это изначально. Это служит для определения сопродукт в , когда он существует.
Дополнения
Ловер показал, что функторы и находятся прилегающий тогда и только тогда, когда категории запятых и , с и тождественные функторы на и соответственно, изоморфны, и эквивалентные элементы в категории запятая могут быть спроецированы на тот же элемент . Это позволяет описывать дополнения без привлечения множеств и фактически было первоначальной мотивацией для введения категорий запятых.
Природные преобразования
Если домены равны, то диаграмма, определяющая морфизмы в с идентична диаграмме, которая определяет естественная трансформация . Разница между этими двумя понятиями состоит в том, что естественное преобразование - это особый набор морфизмов типа вида , а объекты категории запятая содержат все морфизмы типа такой формы. Функтор категории запятая выбирает этот конкретный набор морфизмов. Это кратко описано в наблюдении С.А.Хука.[3]что естественное преобразование , с , соответствует функтору который отображает каждый объект к и отображает каждый морфизм к . Это биективный соответствие между естественными преобразованиями и функторы которые разделы обоих забывчивых функторов из .
Рекомендации
- ^ а б c Адамек, Иржи; Херрлих, Хорст; Стрекер, Джордж Э. (1990). Абстрактные и конкретные категории (PDF). Джон Вили и сыновья. ISBN 0-471-60922-6.
- ^ Ридхард, Дэвид Э .; Берстолл, Род М. (1988). Вычислительная теория категорий (PDF). Прентис Холл.
- ^ Мак-Лейн, Сондерс (1998), Категории для рабочего математика, Тексты для выпускников по математике 5 (2-е изд.), Springer-Verlag, p. 48, ISBN 0-387-98403-8
- Категория запятых в nLab
- Ловер, Вт (1963). «Функториальная семантика алгебраических теорий» и «Некоторые алгебраические проблемы в контексте функциональной семантики алгебраических теорий». http://www.tac.mta.ca/tac/reprints/articles/5/tr5.pdf
внешняя ссылка
Эта статья использование внешняя ссылка может не следовать политикам или рекомендациям Википедии. (Июль 2014 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |
- Дж. Адамек, Х. Херрлих, Г. Штеккер, Абстрактная и конкретная категории - радость кошек
- WildCats пакет теории категорий для Mathematica. Манипуляция и визуализация объектов, морфизмы, категории, функторы, естественные преобразования, универсальные свойства.
- Интерактивная веб-страница который порождает примеры категориальных конструкций в категории конечных множеств.






























































































































