Пять лемм - Википедия - Five lemma
В математика, особенно гомологическая алгебра и другие приложения абелева категория теория, пять лемм является важным и широко используемым лемма о коммутативные диаграммы Лемма о пяти верна не только для абелевых категорий, но и работает в категория групп, Например.
Лемму о пяти можно рассматривать как комбинацию двух других теорем: четыре леммы, которые двойной друг другу.
Заявления
Рассмотрим следующие коммутативная диаграмма в любом абелева категория (например, категория абелевы группы или категория векторные пространства над данным поле ) или в категории группы.
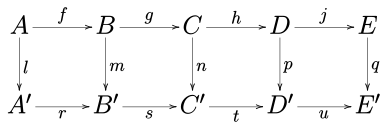
Лемма пяти утверждает, что если строки точный, м и п находятся изоморфизмы, л является эпиморфизм, и q это мономорфизм, тогда п также является изоморфизмом.
Две четыре леммы утверждают:
(1) Если строки коммутативной диаграммы
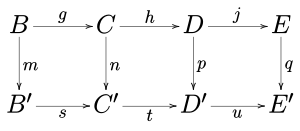
точны и м и п являются эпиморфизмами и q является мономорфизмом, то п это эпиморфизм.
(2) Если строки коммутативной диаграммы

точны и м и п являются мономорфизмами и л является эпиморфизмом, то п является мономорфизмом.
Доказательство
Метод доказательства, который мы будем использовать, обычно называют погоня за диаграммой.[1] Мы докажем пять лемм, отдельно доказывая каждую из двух четырех лемм.
Чтобы выполнить поиск диаграмм, мы предполагаем, что находимся в категории модули над некоторыми звенеть, так что мы можем говорить о элементы объектов на диаграмме и думайте о морфизмах диаграммы как функции (по факту, гомоморфизмы ), действующий на эти элементы, тогда морфизм - это мономорфизм если и только если это инъективный, и это эпиморфизм тогда и только тогда, когда он сюръективный. Точно так же, чтобы иметь дело с точностью, мы можем думать о ядра и изображений в теоретико-функциональном смысле. Доказательство будет по-прежнему применимо к любой (малой) абелевой категории, поскольку Теорема вложения Митчелла, который утверждает, что любая малая абелева категория может быть представлена как категория модулей над некоторым кольцом. Для категории групп просто превратите все аддитивные обозначения ниже в мультипликативные обозначения и обратите внимание, что коммутативность абелевой группы никогда не используется.
Итак, чтобы доказать (1), предположим, что м и п сюръективны и q инъективно.


- Позволять c ′ быть элементом C ′.
- С п сюръективно, существует элемент d в D с п(d) = т(c ′).
- По коммутативности диаграммы ты(п(d)) = q(j(d)).
- Поскольку я т = ker ты по точности 0 = ты(т(c ′)) = ты(п(d)) = q(j(d)).
- С q инъективен, j(d) = 0, поэтому d в кере j = им час.
- Следовательно, существует c в C с час(c) = d.
- потом т(п(c)) = п(час(c)) = т(c ′). С т является гомоморфизмом, то т(c ′ − п(c)) = 0.
- По точности, c ′ − п(c) находится в образе s, значит, существует б ' в B ′ с s(б ') = c ′ − п(c).
- С м сюръективно, мы можем найти б в B такой, что б ' = м(б).
- По коммутативности, п(грамм(б)) = s(м(б)) = c ′ − п(c).
- С п является гомоморфизмом, п(грамм(б) + c) = п(грамм(б)) + п(c) = c ′ − п(c) + п(c) = c ′.
- Следовательно, п сюръективно.
Тогда для доказательства (2) предположим, что м и п инъективны и л сюръективно.

- Позволять c в C быть таким, чтобы п(c) = 0.
- т(п(c)) тогда 0.
- По коммутативности, п(час(c)) = 0.
- С п инъективен, час(c) = 0.
- По точности есть элемент б из B такой, что грамм(б) = c.
- По коммутативности, s(м(б)) = п(грамм(б)) = п(c) = 0.
- По точности тогда существует элемент а ' из A ′ такой, что р(а ') = м(б).
- С л сюръективно, есть а в А такой, что л(а) = а '.
- По коммутативности м(ж(а)) = р(л(а)) = м(б).
- С м инъективен, ж(а) = б.
- Так c = грамм(ж(а)).
- Поскольку состав грамм и ж тривиально, c = 0.
- Следовательно, п инъективно.
Объединение двух четырех лемм доказывает всю лемму из пяти.
Приложения
Лемма пяти часто применяется к длинные точные последовательности: при вычислении гомология или когомологии данного объекта, обычно используется более простой подобъект, гомологии / когомологии которого известны, и получается длинная точная последовательность, которая включает неизвестные группы гомологий исходного объекта. Одного этого часто недостаточно для определения неизвестных групп гомологий, но если можно сравнить исходный объект и подобъект с хорошо изученными с помощью морфизмов, то индуцируется морфизм между соответствующими длинными точными последовательностями, и тогда можно будет выполнить пять лемм. использоваться для определения неизвестных групп гомологии.
Смотрите также
- Лемма короткая пятерка, частный случай леммы пяти для короткие точные последовательности
- Лемма о змее, еще одна лемма, доказываемая поиском диаграмм
- Девять лемм
Примечания
- ^ Мэсси (1991). Базовый курс алгебраической топологии. п. 184.
Рекомендации
- В. Р. Скотт: Теория групп, Прентис-Холл, 1964.
- Мэсси, Уильям С. (1991), Базовый курс алгебраической топологии, Выпускные тексты по математике, 127 (3-е изд.), Springer, ISBN 978-0-387-97430-9


