Нечетный график - Odd graph
| Нечетный график | |
|---|---|
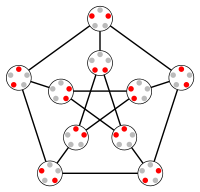 О3 = Кг5,2 это граф Петерсена | |
| Вершины | |
| Края | |
| Диаметр | п − 1[1][2] |
| Обхват | 3 если п = 2 5 если п = 3 6 если п > 3[3] |
| Характеристики | Дистанционно-транзитивный |
| Обозначение | Оп |
| Таблица графиков и параметров | |

в математический поле теория графов, то нечетные графики Оп семья симметричные графы с высоким странный обхват, определенные из определенных установить системы. Они включают и обобщают Граф Петерсена.
Определение и примеры
Нечетный график Оп имеет по одной вершине для каждого из (п - 1) -элементные подмножества a (2п - 1) -элементный набор. Две вершины соединены ребром тогда и только тогда, когда соответствующие подмножества непересекающийся.[4] Это, Оп это Граф Кнезера КГ(2п − 1,п − 1).
О2 это треугольник, а О3 знакомый Граф Петерсена.
В обобщенные нечетные графы определяются как дистанционно регулярные графы с диаметр п - 1 и нечетный обхват 2п - 1 для некоторых п.[5] К ним относятся нечетные графики и свернутые кубические графы.
История и приложения
Хотя граф Петерсена известен с 1898 года, его определение как нечетного графа восходит к работе Ковалевский (1917), который также изучал нечетный граф О4.[2][6]Нечетные графы были изучены для их приложений в химическая теория графов, при моделировании сдвигов ионы карбония.[7][8] Их также предлагали в качестве топология сети в параллельные вычисления.[9]
Обозначение Оп для этих графов был введен Норман Биггс в 1972 г.[10] Биггс и Тони Гардинер объясните название нечетных графов в неопубликованной рукописи 1974 года: каждому ребру нечетного графа может быть присвоен уникальный элемент Икс какой "странный мужчина ", т. е. не входит ни в одно из подмножеств, связанных с вершинами, инцидентными этому ребру.[11][12]
Характеристики
Нечетный график Оп имеет степень п. Она имеет вершины и края. Следовательно, количество вершин для п = 1, 2, ... есть
Расстояние и симметрия
Если две вершины в Оп соответствуют множествам, которые отличаются друг от друга удалением k элементы из одного набора и добавление k различных элементов, то они могут быть достигнуты друг от друга за 2k шаги, каждая пара которых выполняет одно добавление и удаление. Если 2k < п, это кратчайший путь; в противном случае будет короче найти путь этого типа от первого набора к набору, дополнительному ко второму, а затем достичь второго набора еще на один шаг. Следовательно диаметр из Оп является п − 1.[1][2]
Каждый нечетный граф 3-дуговые переходные: каждый ориентированный трехреберный путь в нечетном графе может быть преобразован в любой другой такой путь посредством симметрии графа.[13]Нечетные графики переходное расстояние, следовательно дистанция регулярная.[2] Как дистанционно регулярные графы, они однозначно определяются своим массивом пересечений: никакие другие дистанционно регулярные графы не могут иметь такие же параметры, как нечетный граф.[14] Однако, несмотря на высокую степень симметрии, нечетные графы Оп за п > 2 никогда Графики Кэли.[15]
Поскольку нечетные графы регулярны и реберно-транзитивный, их связность вершин равняется их степени, п.[16]
Нечетные графики с п > 3 имеют обхват шесть; однако, хотя они не двудольные графы, их странные циклы намного длиннее. В частности, нечетный граф Оп имеет странный обхват 2п - 1. Если п-регулярный граф имеет диаметр п - 1 и нечетный обхват 2п - 1 и имеет только п отчетливый собственные значения, он должен быть регулярным. Дистанционно регулярные графы с диаметром п - 1 и нечетный обхват 2п - 1 известны как обобщенные нечетные графы, и включить свернутые кубические графы а также сами нечетные графы.[5]
Независимые множества и раскраска вершин
Позволять Оп - нечетный граф, определенный из подмножеств (2п - 1) -элементный комплект Икс, и разреши Икс быть любым членом Икс. Тогда среди вершин Оп, точно вершины соответствуют множествам, содержащимИкс. Поскольку все эти наборы содержат Икс, они не пересекаются и образуют независимый набор из Оп. Это, Оп имеет 2п - 1 разные независимые наборы размеров . Это следует из Теорема Эрдеша – Ко – Радо. что это максимальные независимые множества из Оп. это число независимости из Оп является Кроме того, каждый максимальный независимый набор должен иметь такую форму, поэтому Оп имеет ровно 2п - 1 максимум независимых комплектов.[2]
Если я - максимальное независимое множество, образованное наборами, содержащими Икс, то дополнять из я - это множество вершин, не содержащих Икс. Этот дополнительный набор побуждает а соответствие в г. Каждая вершина независимого множества смежна с п вершины совпадения, и каждая вершина совпадения смежна с п - 1 вершина независимого множества.[2] Из-за этого разложения и из-за того, что нечетные графы не являются двудольными, они имеют хроматическое число три: вершинам максимального независимого набора может быть назначен один цвет, и еще двух цветов достаточно, чтобы раскрасить дополнительное соответствие.
Краска окраски
К Теорема Визинга, количество цветов, необходимое для раскрасьте края нечетного графа Оп либо п или п + 1, а в случае графа Петерсена О3 это п + 1. Когда п является степенью двойки, количество вершин в графе нечетное, из чего снова следует, что количество цветов ребер равно п + 1.[17] Однако, О5, О6, и О7 каждый может быть окрашен по краю п цвета.[2][17]
Биггс[10] объясняет эту проблему следующей историей: одиннадцать футбольный игроки в вымышленном городе Кроам хотят собрать пары команды по пять человек (со странным человеком, работающим в качестве судьи) всеми 1386 возможными способами, и они хотят запланировать игры между каждой парой таким образом, чтобы шесть игр каждой команды игрались в шесть разных дней недели, с воскресеньями. выкл для всех команд. Возможно ли это сделать? В этой истории каждая игра представляет собой край О6, каждый будний день представлен цветом, а крайняя 6-цветная окраска О6 обеспечивает решение проблемы расписания игроков.
Гамильтоничность
Граф Петерсена О3 хорошо известный негамильтонов граф, но все нечетные графы Оп за п ≥ 4, как известно, имеют гамильтонов цикл.[18]Поскольку нечетные графики вершинно-транзитивный, они, таким образом, являются одним из частных случаев, когда положительный ответ на Гипотеза Ловаса известен. Биггс[2] предположил в более общем смысле, что края Оп можно разделить на реберно-непересекающиеся гамильтоновы циклы. Когда п является нечетным, тогда оставшиеся края должны образовывать идеальное совпадение. Эта более сильная гипотеза была проверена для п = 4, 5, 6, 7.[2][17] За п = 8, нечетное количество вершин в Оп предотвращает 8-цветовую раскраску ребер, но не исключает возможности разбиения на четыре гамильтоновых цикла.
Рекомендации
- ^ а б Биггс, Норман Л. (1976), "Автоморфные графы и условие Крейна", Geometriae Dedicata, 5 (1): 117–127, Дои:10.1007 / BF00148146.
- ^ а б c d е ж грамм час я Биггс, Норман (1979), "Некоторая теория нечетных графов", Вторая международная конференция по комбинаторной математике, Летопись Нью-Йоркской академии наук, 319: 71–81, Дои:10.1111 / j.1749-6632.1979.tb32775.x.
- ^ Уэст, Дуглас Б. (2000), «Упражнение 1.1.28», Введение в теорию графов (2-е изд.), Englewood Cliffs, NJ: Prentice-Hall, p. 17.
- ^ Вайсштейн, Эрик В. «Нечетный график». MathWorld.
- ^ а б Ван Дам, Эдвин; Хемерс, Виллем Х. (2010), Нечетная характеристика обобщенных нечетных графов, CentER Discussion Paper Series No. 2010-47, SSRN 1596575.
- ^ Ковалевски, А. (1917), "Dodekaederaufgabe als Buntordnungproblem У. Р. Гамильтона", Sitzungsber. Акад. Wiss. Вена (Abt. IIa), 126: 67–90, 963–1007. Как цитирует Биггс (1979).
- ^ Балабан, Александру Т .; Fǎrcaşiu, D .; Bǎnic, R. (1966), "Графики множественных 1,2-сдвигов в ионах карбония и родственных системах", Преподобный Рум. Чим., 11: 1205.
- ^ Балабан, Александру Т. (1972), "Химические графики, Часть XIII: Комбинаторные шаблоны", Rev. Roumaine Math. Pures Appl., 17: 3–16.
- ^ Гафур, Ариф; Башков, Теодор Р. (1991), "Исследование нечетных графов как отказоустойчивых сетей межсоединений", Транзакции IEEE на компьютерах, 40 (2): 225–232, Дои:10.1109/12.73594.
- ^ а б Биггс, Норман (1972), Гай, Ричард К. (ред.), "Проблема раскраски ребер", Проблемы исследования, Американский математический ежемесячный журнал, 79 (9): 1018–1020, Дои:10.2307/2318076, JSTOR 2318076.
- ^ Брауэр, Андрис; Cohen, Arjeh M .; Ноймайер, А. (1989), Дистанционно регулярные графы, ISBN 0-387-50619-5.
- ^ Эд Пегг младший (29 декабря 2003 г.), Кубические симметричные графы, Математические игры, Математическая ассоциация Америки, заархивировано из оригинал 21 августа 2010 г., получено 24 августа, 2010.
- ^ Бабай, Ласло (1995), "Группы автоморфизмов, изоморфизм, реконструкция", в Грэм, Рональд Л.; Грётшель, Мартин; Ловас, Ласло (ред.), Справочник по комбинаторике, я, North-Holland, стр. 1447–1540, Предложение 1.9, архивировано из оригинал 11 июня 2010 г..
- ^ Луна, Aeryung (1982), "Характеристика нечетных графов Оk по параметрам », Дискретная математика, 42 (1): 91–97, Дои:10.1016 / 0012-365X (82) 90057-7.
- ^ Годсил, К. Д. (1980), "Более странная теория графов", Дискретная математика, 32 (2): 205–207, Дои:10.1016 / 0012-365X (80) 90055-2.
- ^ Уоткинс, Марк Э. (1970), "Связность транзитивных графов", Журнал комбинаторной теории, 8: 23–29, Дои:10.1016 / S0021-9800 (70) 80005-9, Г-Н 0266804
- ^ а б c Мередит, Гай Х. Дж .; Ллойд, Э. Кейт (1973), «Футболисты Кроама», Журнал комбинаторной теории, серия B, 15 (2): 161–166, Дои:10.1016/0095-8956(73)90016-6.
- ^ Мютце, Торстен; Нумменпало, Джерри; Вальчак, Бартош (2018), «Разреженные графы Кнезера гамильтоновы», STOC'18 - Материалы 50-го ежегодного симпозиума ACM SIGACT по теории вычислений, Нью-Йорк: ACM, стр. 912–919, arXiv:1711.01636, Г-Н 3826304





