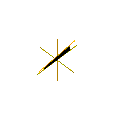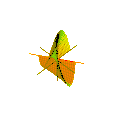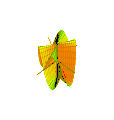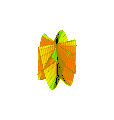Коноид Плюккерса - Википедия - Plückers conoid

Рис. 1. Коноид Плюккера с п=2.
Рис. 2. Коноид Плюккера с п = 3.
Рис. 3. Коноид Плюккера с п = 4.

В геометрия, Коноид Плюккера это линейчатая поверхность назван в честь немецкого математика Юлиус Плюкер. Его также называют конический клин или же цилиндроид; однако последнее название неоднозначно, так как "цилиндроид" может также относиться к эллиптический цилиндр.

Коноид Плюккера - это поверхность, определяемая функцией двух переменных:

Эта функция имеет существенная особенность на источник.

Используя цилиндрические координаты в пространстве, мы можем записать указанную выше функцию в параметрические уравнения

Таким образом, коноид Плюккера является правый коноид, которую можно получить, вращая горизонтальную линию вокруг оси z при колебательном движении (с периодом 2π) вдоль отрезка [−1, 1] оси (рисунок 4).

Обобщение коноида Плюккера дается параметрическими уравнениями

куда п обозначает количество складок на поверхности. Отличие в том, что период колебательного движения по z- ось 2π/п. (Рисунок 5 для п = 3)

Рис. 4. Коноид Плюккера с п = 2.
Рис. 5. Коноид Плюккера с п = 3

  • Анимация коноида Плюккера с n = 2

  • Коноид Плюккера с n = 2

  • Коноид Плюккера n = 3

  • Анимация коноида Плюккера с n = 2

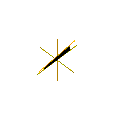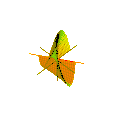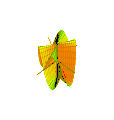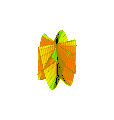
  • Анимация коноида Плюккера с n = 3

  • Коноид Плюккера n = 4

Смотрите также

Рекомендации

  • А. Грей, Э. Аббена, С. Саламон, Современная дифференциальная геометрия кривых и поверхностей в системе Mathematica, 3-е изд. Бока-Ратон, Флорида: CRC Press, 2006. [1] (ISBN  978-1-58488-448-4)
  • Владимир Юрьевич Ровенский, Геометрия кривых и поверхностей с MAPLE [2] (ISBN  978-0-8176-4074-3)

внешняя ссылка