Полупорядок - Semiorder

В Диаграмма Хассе полупорядка. Два элемента можно сравнить, если их вертикальные координаты отличаются хотя бы на одну единицу (расстояние между сплошными синими линиями).

В теория порядка, раздел математики, полурядный - это тип упорядочения элементов с числовыми оценками, при котором элементы с сильно различающимися оценками сравниваются по своим оценкам, а оценки в пределах заданного погрешность считаются несравненный. Полупорядки были введены и применены в математическая психология к Дункан Люс (1956 ) как модель человеческих предпочтений. Они обобщают строгие слабые порядки, в котором пункты с равными баллами могут быть равны, но нет права на ошибку. Они являются частным случаем частичные заказы и из интервальные заказы, и может быть охарактеризована среди частичных заказов дополнительными аксиомы, или двумя запрещенными четырехпозиционными подотрядами.

Определение

Аксиома 2

Аксиома 3

Позволять Икс будет набором элементов, и пусть <будет бинарное отношение на Икс.Предметы Икс и у как говорят несравненныйздесь написано как Икс ~ у, если ни Икс < у ни у < Икс правда. Тогда пара (Икс, <) является полупорядком, если он удовлетворяет следующим трем аксиомам:^[1]

Для всех Икс и у, это невозможно для обоих Икс < у и у < Икс быть правдой. То есть <должен быть асимметричное отношение
Для всех Икс, у, z, и ш, если Икс < у, у ~ z, и z < ш, тогда Икс < ш.
Для всех Икс, у, z, и ш, если Икс < у и у < z, то либо Икс < ш или же ш < z. Эквивалентно, с теми же предположениями о Икс, у, z, любой другой предмет ш должен быть сопоставим хотя бы с одним из Икс, у, или же z.

Из первой аксиомы следует, что Икс ~ Икс, а значит, и вторая аксиома (с у = z) следует, что <является переходное отношение.

Через запрещенные подзаказы

А частичный заказ является полупорядком тогда и только тогда, когда он не содержит следующих двух частичных порядков в качестве подотряда.^[2]

Запрещенные подзаказы для полупорядков

Отношение к другим видам заказа

Частичные заказы

Можно определить частичный заказ (Икс, ≤) из полупорядка (Икс, <), объявив, что Икс ≤ у когда либо Икс < у или же Икс = у. Из аксиом, для выполнения которых требуется частичный порядок, рефлексивность (Икс ≤ Икс) автоматически следует из этого определения, антисимметрия (если Икс ≤ у и у ≤ Икс тогда Икс = у) следует из аксиомы первого полупорядка, а транзитивность (если Икс ≤ у и у ≤ z тогда Икс ≤ z) следует из второй аксиомы полупорядка. И наоборот, из определенного таким образом частичного порядка можно восстановить полупорядок, объявив, что Икс < у в любое время Икс ≤ у и Икс ≠ у. Первая из перечисленных выше аксиом полупорядка автоматически следует из аксиом, определяющих частичный порядок, а остальные - нет. Вторая и третья аксиомы полупорядка запрещают частичные порядки из четырех элементов, образующих две непересекающиеся цепочки: вторая аксиома запрещает две цепочки по два элемента в каждой, а третья элемент запрещает цепочку из трех элементов с одним несвязанным элементом.

Слабые приказы

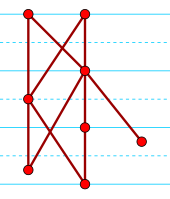
Всякий строгий слабый порядок <также является полупорядком. В частности, транзитивность <и транзитивность несравнимости относительно <вместе подразумевают указанную выше аксиому 2, в то время как транзитивность одной только несравнимости влечет аксиому 3. Полупорядок, показанный на верхнем изображении, не является строгим слабым порядком, поскольку самая правая вершина несравнима с двумя его ближайшими левыми соседями, но они сопоставимы.

Интервальные заказы

Отношение является полупорядком тогда и только тогда, когда оно может быть получено как интервальный порядок интервалов единичной длины ${ displaystyle ( ell _ {i}, ell _ {i} +1)}$ .

Квазитранзитивные отношения

В соответствии с Амартья К. Сен,^[3] полузаказы были рассмотрены Дин Т. Джеймисон и Лоуренс Дж. Лау^[4] и оказался частным случаем квазитранзитивные отношения. Фактически, любой полупорядок является квазитранзитивным отношением, поскольку он транзитивен. Более того, добавление к заданному полупорядку всех его пар несравнимых элементов сохраняет результирующее отношение квазитранзитивным.^[5]

Теория полезности

Первоначальная мотивация для введения полупорядков заключалась в моделировании человеческих предпочтений без предположения (как это делают строгие слабые порядки), что несравнимость является переходное отношение. Например, если Икс, у, и z представляют три количества одного и того же материала, и Икс и z отличаются наименьшей величиной, заметной как разница, в то время как у находится на полпути между ними двумя, тогда разумно предпочтение между Икс и z но не между двумя другими парами, нарушая транзитивность.^[6]

Итак, предположим, что Икс это набор предметов, а ты это вспомогательная функция который отображает членов Икс к действительные числа. Строгий слабый порядок можно определить на Икс объявляя два объекта несравнимыми, если они имеют равную полезность, и в противном случае используя численное сравнение, но это обязательно приводит к переходному отношению несравнимости. Вместо этого, если установить числовой порог (который может быть нормализован до 1), так что полезности в пределах этого порога друг друга объявляются несравнимыми, тогда возникает полупорядок.

В частности, определите бинарное отношение <из Икс и ты установив Икс < у в любое время ты(Икс) ≤ ты(у) - 1. Тогда (Икс, <) - полупорядок.^[7] Его можно эквивалентно определить как интервальный порядок определяется интервалами [ты(Икс),ты(Икс) + 1].^[8]

С другой стороны, не каждый полупорядок может быть определен таким образом с помощью числовых утилит. Например, если полупорядок (Икс, <) включает бесчисленный полностью упорядоченное подмножество тогда не существует достаточно большого числа действительных чисел с достаточно большим интервалом, чтобы представить это подмножество в числовом виде. Однако любой конечный полупорядок можно определить из функции полезности.^[9] Фишберн (1973) предоставляет точную характеристику полупорядков, которая может быть определена численно.

Если полупорядок задан только в терминах отношения порядка между его парами элементов, то можно построить функцию полезности, которая представляет порядок во времени. $О (п 2)$ , куда $п$ - количество элементов в полупорядке.^[10]

Комбинаторное перечисление

Количество отличных полупорядков на п немаркированные предметы даются Каталонские числа

{ displaystyle { frac {1} {n + 1}} { binom {2n} {n}},}

^[11]

а количество полурядок на п отмеченные элементы задаются последовательностью

1, 1, 3, 19, 183, 2371, 38703, 763099, 17648823, ... (последовательность A006531 в OEIS ).^[12]

Другие результаты

Любой конечный полупорядок имеет размер заказа максимум три.^[13]

Среди всех частичных порядков с фиксированным количеством элементов и фиксированным количеством сопоставимых пар частичные порядки, которые имеют наибольшее количество линейные расширения являются полупорядками.^[14]

Известно, что полупорядки подчиняются 1 / 3–2 / 3 гипотеза: в любом конечном полупорядке, который не является полным порядком, существует пара элементов Икс и у такой, что Икс появляется раньше, чем у между 1/3 и 2/3 линейных расширений полупорядка.^[2]

Набор полупорядков на п-элементный набор есть хорошо оцененный: если два полугруппы в одном наборе отличаются друг от друга добавлением или удалением k порядка отношений, то можно найти путь k шаги от первого полупорядка ко второму таким образом, что каждый шаг пути добавляет или удаляет одно отношение порядка, а каждое промежуточное состояние в пути само является полупорядком.^[15]

В графы несравнимости полупорядков называются графики безразличия, и являются частным случаем интервальные графики.^[16]

Примечания

^ Люс (1956) описывает эквивалентный набор из четырех аксиом, первые две из которых объединяют определение несравнимости и первую аксиому, перечисленные здесь.
^ ^а ^б Брайтвелл (1989).
^ Сен (1971, Раздел 10, с. 314) Поскольку Люси смоделировала безразличие между Икс и у как "ни xRy ни yRx", а Сен смоделировал это как" оба xRy и yRx", Замечание Сена на стр. 314, вероятно, имеет в виду последнее свойство.
^ Джеймисон и Лау (1970).
^ Бургхардт (2018), Лемма 20, с. 27.
^ Люс (1956), п. 179.
^ Люс (1956) Теорема 3 описывает более общую ситуацию, в которой порог сравнимости между двумя полезностями является функцией полезности, а не равен 1.
^ Фишберн (1970).
^ Этот результат обычно приписывается Скотт и Суппес (1958); см., например, Рабинович (1977). Тем не мение, Люс (1956) Теорема 2 доказывает более общее утверждение, что конечный полупорядок может быть определен из функции полезности и пороговой функции всякий раз, когда некоторый базовый слабый порядок может быть определен численно. Для конечных полупорядков нетривиально то, что слабый порядок можно определить численно с помощью единичной пороговой функции.
^ Эйвери (1992).
^ Ким и Роуш (1978).
^ Шандон, Лемэр и Пуже (1978).
^ Рабинович (1978).
^ Фишберн и Троттер (1992).
^ Дуаньон и Фальмань (1997).
^ Робертс (1969).

дальнейшее чтение

Пирло, М .; Винке, доктор наук (1997), Полупорядки: свойства, представления, приложения, Теория и библиотека решений. Серия B: Математические и статистические методы, 36, Дордрехт: Kluwer Academic Publishers Group, ISBN 0-7923-4617-3, МИСТЕР 1472236.

[1] Люс (1956) описывает эквивалентный набор из четырех аксиом, первые две из которых объединяют определение несравнимости и первую аксиому, перечисленные здесь.

[:0-2] а ^б Брайтвелл (1989).

[3] Сен (1971, Раздел 10, с. 314) Поскольку Люси смоделировала безразличие между Икс и у как "ни xRy ни yRx", а Сен смоделировал это как" оба xRy и yRx", Замечание Сена на стр. 314, вероятно, имеет в виду последнее свойство.

[FOOTNOTEJamisonLau1970-4] Джеймисон и Лау (1970).

[FOOTNOTEBurghardt2018Lemma_20,_p._27-5] Бургхардт (2018), Лемма 20, с. 27.

[6] Люс (1956), п. 179.

[7] Люс (1956) Теорема 3 описывает более общую ситуацию, в которой порог сравнимости между двумя полезностями является функцией полезности, а не равен 1.

[8] Фишберн (1970).

[9] Этот результат обычно приписывается Скотт и Суппес (1958); см., например, Рабинович (1977). Тем не мение, Люс (1956) Теорема 2 доказывает более общее утверждение, что конечный полупорядок может быть определен из функции полезности и пороговой функции всякий раз, когда некоторый базовый слабый порядок может быть определен численно. Для конечных полупорядков нетривиально то, что слабый порядок можно определить численно с помощью единичной пороговой функции.

[FOOTNOTEAvery1992-10] Эйвери (1992).

[11] Ким и Роуш (1978).

[12] Шандон, Лемэр и Пуже (1978).

[13] Рабинович (1978).

[14] Фишберн и Троттер (1992).

[15] Дуаньон и Фальмань (1997).

[FOOTNOTERoberts1969-16] Робертс (1969).

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]