Раздавленное запутывание - Squashed entanglement

Раздавленное запутывание, также называемый CMI запутанность (CMI можно произносить как «увидеть меня»), это теоретико-информационная мера квантовая запутанность для двудольной квантовой системы. Если ${displaystyle varrho _ {A, B}}$ это матрица плотности системы ${displaystyle (A, B)}$ состоит из двух подсистем ${displaystyle A}$ и ${displaystyle B}$, то запутанность CMI ${displaystyle E_ {CMI}}$ системы ${displaystyle (A, B)}$ определяется

${displaystyle E_ {CMI} (varrho _ {A, B}) = {frac {1} {2}} min _ {varrho _ {A, B, Lambda} in K} S (A: B | Lambda)}$,

Уравнение (1)

куда ${displaystyle K}$ - множество всех матриц плотности ${displaystyle varrho _ {A, B, Lambda}}$ для трехсторонней системы ${displaystyle (A, B, Lambda)}$ такой, что ${displaystyle varrho _ {A, B} = tr_ {Lambda} (varrho _ {A, B, Lambda})}$. Таким образом, запутанность CMI определяется как экстремум функциональный ${displaystyle S (A: B | Lambda)}$ из ${displaystyle varrho _ {A, B, Lambda}}$. Мы определяем ${displaystyle S (A: B | Lambda)}$квантовая Условная взаимная информация (CMI), ниже. Более общая версия уравнения (1) заменяет "min" (минимум) в уравнении (1) на "inf" (инфимум ). Когда ${displaystyle varrho _ {A, B}}$ чистое состояние, ${displaystyle E_ {CMI} (varrho _ {A, B}) = S (varrho _ {A}) = S (varrho _ {B})}$, в соответствии с определением запутанность формации для чистых состояний. Здесь ${displaystyle S (varrho)}$ это Энтропия фон Неймана матрицы плотности ${displaystyle varrho}$.

Мотивация для определения запутанности CMI

Запутанность CMI имеет свои корни в классическая (неквантовая) теория информации, как мы объясним далее.

Учитывая любые два случайные переменные ${displaystyle A, B}$классическая теория информации определяет взаимная информация, мера корреляций, как

${displaystyle H (A: B) = H (A) + H (B) -H (A, B),}$.

Уравнение (2)

Для трех случайных величин ${displaystyle A, B, Lambda}$, он определяет CMI как

${displaystyle {egin {matrix} H (A: B | Lambda) & = & H (A | Lambda) + H (B | Lambda) -H (A, B | Lambda) & = & H (A, Lambda) + H (B, лямбда) -H (лямбда) -H (A, B, лямбда) конец {матрица}}}$.

Уравнение (3)

Можно показать, что ${displaystyle H (A: B | Lambda) geq 0}$.

Теперь предположим ${displaystyle varrho _ {A, B, Lambda}}$ - матрица плотности трехчастной системы ${displaystyle (A, B, Lambda)}$. Мы будем представлять частичный след из ${displaystyle varrho _ {A, B, Lambda}}$ по отношению к одной или двум его подсистемам ${displaystyle varrho _ {A, B, Lambda}}$ со стертым символом отслеживаемой системы. Например, ${displaystyle varrho _ {A, B} = tr_ {Lambda} (varrho _ {A, B, Lambda})}$. Квантовый аналог уравнения (2) можно определить следующим образом:

${displaystyle S (A: B) = S (varrho _ {A}) + S (varrho _ {B}) - S (varrho _ {A, B}),}$,

Уравнение (4)

и квантовый аналог уравнения (3) формулой

${displaystyle S (A: B | Lambda) = S (varrho _ {A, Lambda}) + S (varrho _ {B, Lambda}) - S (varrho _ {Lambda}) - S (varrho _ {A, B , Лямбда}),}$.

Уравнение (5)

Можно показать, что ${displaystyle S (A: B | Lambda) geq 0}$. Это неравенство часто называют сильная субаддитивность свойство квантовой энтропии.

Рассмотрим три случайные величины ${displaystyle A, B, Lambda}$ с распределением вероятностей ${displaystyle P_ {A, B, Lambda} (a, b, lambda)}$, который мы будем сокращать как ${displaystyle P (a, b, lambda)}$. Для тех, кто особенный ${displaystyle P (a, b, lambda)}$ формы

${displaystyle P (a, b, lambda) = P (a | lambda) P (b | lambda) P (lambda),}$,

Уравнение (6)

Рис.1: Байесовская сеть, представление уравнения (6)

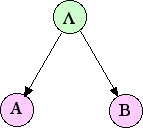
можно показать, что ${displaystyle H (A: B | Lambda) = 0}$. Распределения вероятностей вида (6) на самом деле описываются Байесовская сеть показано на рис.1.

Классическую запутанность CMI можно определить следующим образом:

${displaystyle E_ {CMI} (P_ {A, B}) = min _ {P_ {A, B, Lambda} in K} H (A: B | Lambda)}$,

Уравнение (7)

куда ${displaystyle K}$ - это множество всех вероятностных распределений ${displaystyle P_ {A, B, Lambda}}$ в трех случайных величинах ${displaystyle A, B, Lambda}$, так что ${displaystyle sum _ {lambda} P_ {A, B, Lambda} (a, b, lambda) = P_ {A, B} (a, b),}$для всех ${displaystyle a, b}$. Потому что, учитывая распределение вероятностей ${displaystyle P_ {A, B}}$, всегда можно продолжить его до распределения вероятностей ${displaystyle P_ {A, B, Lambda}}$ который удовлетворяет уравнению (6)^{[нужна цитата ]}, следует, что классическая CMI-запутанность, ${displaystyle E_ {CMI} (P_ {A, B})}$, равна нулю для всех ${displaystyle P_ {A, B}}$. Дело в том, что ${displaystyle E_ {CMI} (P_ {A, B})}$ всегда исчезает - важная мотивация для определения ${displaystyle E_ {CMI} (varrho _ {A, B})}$. Нам нужна мера квантовой запутанности, которая исчезает в классическом режиме.

Предполагать ${displaystyle w_ {lambda}}$ за ${displaystyle lambda = 1,2, ..., dim (лямбда)}$ представляет собой набор неотрицательных чисел, которые в сумме составляют единицу, и ${displaystyle | lambda angle}$ за ${displaystyle lambda = 1,2, ..., dim (лямбда)}$ является ортонормированным базисом гильбертова пространства, связанного с квантовой системой ${displaystyle Lambda}$. Предполагать ${displaystyle varrho _ {A} ^ {lambda}}$ и ${displaystyle varrho _ {B} ^ {lambda}}$, за ${displaystyle lambda = 1,2, ..., dim (лямбда)}$ - матрицы плотности систем ${displaystyle A}$ и ${displaystyle B}$, соответственно. Можно показать, что следующая матрица плотности

${displaystyle varrho _ {A, B, Lambda} = sum _ {lambda} varrho _ {A} ^ {lambda} varrho _ {B} ^ {lambda} w_ {lambda} | langle langle lambda |,}$

Уравнение (8)

удовлетворяет ${displaystyle S (A: B | Lambda) = 0}$. Уравнение (8) является квантовым аналогом уравнения (6). Прослеживая матрицу плотности уравнения (8) по ${displaystyle Lambda}$, мы получили ${displaystyle varrho _ {A, B} = sum _ {lambda} varrho _ {A} ^ {lambda} varrho _ {B} ^ {lambda} w_ {lambda},}$, который является отделимое состояние. Следовательно, ${displaystyle E_ {CMI} (varrho _ {A, B})}$ (1) обращается в нуль для всех сепарабельных состояний.

Когда ${displaystyle varrho _ {A, B}}$ чистое состояние, получается${displaystyle E_ {CMI} (varrho _ {A, B}) = S (varrho _ {A}) = S (varrho _ {B})}$. Это согласуется с определением запутанность формации для чистых состояний, как указано в Ben96.

Далее предположим ${displaystyle | psi _ {A, B} ^ {lambda} angle}$ за ${displaystyle lambda = 1,2, ..., dim (лямбда)}$ некоторые состояния в гильбертовом пространстве, связанные с квантовой системой ${displaystyle (A, B)}$. Позволять ${displaystyle K}$ - набор матриц плотности, определенных ранее для уравнения (1). Определять ${displaystyle K_ {o}}$ быть набором всех матриц плотности ${displaystyle varrho _ {A, B, Lambda}}$ это элементы ${displaystyle K}$ и иметь особую форму ${displaystyle varrho _ {A, B, Lambda} = sum _ {lambda} | psi _ {A, B} ^ {lambda} angle langle psi _ {A, B} ^ {lambda} | w_ {lambda} | lambda angle langle lambda |,}$. Можно показать, что если в уравнении (1) заменить множество ${displaystyle K}$ своим собственным подмножеством ${displaystyle K_ {o}}$, то уравнение (1) сводится к определению запутанности образования для смешанных состояний, как это дано в Ben96. ${displaystyle K}$ и ${displaystyle K_ {o}}$ представляют различные степени знания о том, как ${displaystyle varrho _ {A, B, Lambda}}$ был создан. ${displaystyle K}$ представляет собой полное невежество.

Поскольку запутанность CMI сводится к запутанность формации если свести к минимуму ${displaystyle K_ {o}}$ вместо ${displaystyle K}$можно ожидать, что запутанность CMI наследует многие желательные свойства от запутанности образования.

История

Важное неравенство ${displaystyle S (A: B | Lambda) geq 0}$ был впервые доказан Либом и Рускаем в LR73.

Классический CMI, определяемый уравнением (3), впервые введен теория информации знания, вскоре после основополагающей статьи Шеннона 1948 г. и, по крайней мере, уже в 1954 г. McG54. Квантовый CMI, задаваемый уравнением (5), был впервые определен Серфом и Адами в Cer96. Однако, похоже, Серф и Адами не осознавали связь CMI с запутанностью или возможность получения меры квантовой запутанности на основе CMI; это можно вывести, например, из более поздней статьи, Cer97, где они пытаются использовать ${displaystyle S (A | B)}$ вместо CMI, чтобы понять запутанность. Первая статья, в которой явно указывается на связь между CMI и квантовой запутанностью, выглядит так: Tuc99.

Окончательное определение запутанности CMI (1) было впервые дано Туччи в серии из 6 статей. (См., Например, уравнение (8) Tuc02 и уравнение (42) Tuc01a). В Tuc00b, он указал на классическую вероятностную мотивацию уравнения (1) и его связь с определениями запутанности образования для чистых и смешанных состояний. В Tuc01a, он представил алгоритм и компьютерную программу, основанную на Метод Аримото-Блахута теории информации, для численного расчета запутанности CMI. В Tuc01b, он рассчитал запутанность CMI аналитически для смешанного состояния двух кубиты.

В Сено03, Хайден, Джозса, Петц и Винтер исследовали связь между квантовым CMI и отделимость.

Однако этого не произошло, пока Chr03, что было показано, что запутанность CMI на самом деле является мерой запутанности, т.е. что она не увеличивается при локальных операциях и классической коммуникации (LOCC). Доказательство адаптировано Ben96 аргументы о запутанности образования. В Chr03, они также доказали множество других интересных неравенств, касающихся запутанности CMI, в том числе то, что она аддитивна, и исследовали ее связь с другими мерами запутанности. Название сплющенное запутывание впервые появился в Chr03. В Chr05, Кристандл и Винтер аналитически вычислили CMI-запутанность некоторых интересных состояний.

В Ali03, Алики и Фаннес доказали непрерывность запутанности CMI. В BCY10, Брандао, Кристандл и Ярд показали, что запутанность CMI равна нулю тогда и только тогда, когда состояние разделимо. В Хуа14, Хуанг доказал, что вычисление сжатой запутанности NP-сложно.

Рекомендации

• Ali03 Alicki, R .; Фаннес, М. (2003). «Непрерывность квантовой взаимной информации». J. Phys. А. 37 (55): L55 – L57. arXiv:Quant-ph / 0312081. Bibcode:2004JPhA ... 37L..55A. Дои:10.1088 / 0305-4470 / 37/5 / L01.
• BCY10 Brandao, F .; Christandl, M .; Ярд, Дж. (Сентябрь 2011 г.). «Верное раздавленное запутывание». Коммуникации по математической физике. 306 (3): 805–830. arXiv:1010.1750. Bibcode:2011CMaPh.306..805B. Дои:10.1007 / s00220-011-1302-1.
• Ben96 Беннетт, Чарльз Х .; Ди Винченцо, Дэвид П .; Смолин, Джон А .; Wootters, Уильям К. (1996). «Смешанная запутанность состояний и квантовая коррекция ошибок». Физический обзор A. 54 (5): 3824–3851. arXiv:Quant-ph / 9604024. Bibcode:1996ПхРвА..54.3824Б. Дои:10.1103 / PhysRevA.54.3824. PMID  9913930.
• Cer96 Cerf, N.J .; Адами, К. (1996). «Квантовая механика измерения». arXiv:Quant-ph / 9605002.
• Cer97 Cerf, N.J .; Adami, C .; Гингрич, Р. М. (1999). «Квантовый условный оператор и критерий отделимости». Физический обзор A. 60 (2): 893–898. arXiv:Quant-ph / 9710001. Bibcode:1999PhRvA..60..893C. Дои:10.1103 / PhysRevA.60.893.
• Chr03 Маттиас Кристандл; Андреас Винтер (2003). ""Сдавленное запутывание ": мера аддитивного запутывания". Журнал математической физики. 45 (3): 829–840. arXiv:Quant-ph / 0308088. Bibcode:2004JMP .... 45..829C. Дои:10.1063/1.1643788.
• Chr05 Маттиас Кристандл; Андреас Винтер (2005). «Неопределенность, моногамия и блокировка квантовых корреляций». IEEE Transactions по теории информации. 51 (9): 3159–3165. arXiv:Quant-ph / 0501090. Дои:10.1109 / TIT.2005.853338.
• Chr06 Матиас Кристандл (2006). «Структура двудольных квантовых состояний - выводы из теории групп и криптографии». arXiv:Quant-ph / 0604183. Кембриджская докторская диссертация.
• Сено03 Патрик Хайден; Ричард Джозса; Денес Петц; Андреас Винтер (2004). «Структура состояний, удовлетворяющих сильной субаддитивности квантовой энтропии с равенством». Коммуникации по математической физике. 246 (2): 359–374. arXiv:Quant-ph / 0304007. Bibcode:2004CMaPh.246..359H. Дои:10.1007 / s00220-004-1049-z.
• Хуа14 Хуан, Ичэнь (21 марта 2014 г.). «Вычислительный квантовый диссонанс является NP-полным». Новый журнал физики. 16 (3): 033027. arXiv:1305.5941. Bibcode:2014NJPh ... 16c3027H. Дои:10.1088/1367-2630/16/3/033027.
• LR73 Эллиотт Х. Либ, Мэри Бет Рускай, "Доказательство сильной субаддитивности квантово-механической энтропии", Журнал математической физики 14 (1973) 1938-1941.
• McG54 W.J. McGill, "Многомерная передача информации", IRE Trans. Информация. Теория 4 (1954) 93-111.
• Tuc99 Туччи, Роберт Р. (1999). «Квантовая запутанность и условная передача информации». arXiv:Quant-ph / 9909041.
• Tuc00a Туччи, Роберт Р. (2000). «Разделимость матриц плотности и условная передача информации». arXiv:Quant-ph / 0005119.
• Tuc00b Туччи, Роберт Р. (2000). «Запутанность формирования и условной передачи информации». arXiv:Quant-ph / 0010041.
• Tuc01a Туччи, Роберт Р. (2001). «Релаксационный метод расчета квантовой запутанности». arXiv:Quant-ph / 0101123.
• Tuc01b Туччи, Роберт Р. (2001). «Сплетение колокольных смесей двух кубитов». arXiv:Quant-ph / 0103040.
• Tuc02 Туччи, Роберт Р. (2002). «Запутанность дистилляции и условной взаимной информации». arXiv:Quant-ph / 0202144.

внешняя ссылка

• Верное сплющенное запутывание