Радиус устойчивости - Stability radius

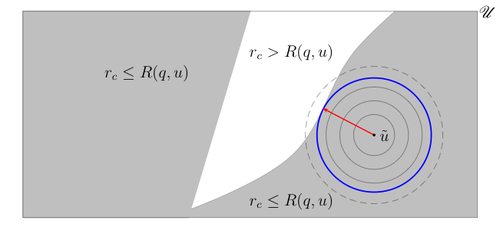
Радиус устойчивости объекта (системы, функции, матрицы, параметра) в заданной номинальной точке - это радиус наибольшего мяч с центром в номинальной точке, все элементы которого удовлетворяют заранее заданным условиям устойчивости. Картина этого интуитивного представления такова:

куда ${ displaystyle { hat {p}}}$ обозначает номинальную точку, ${ displaystyle P}$ обозначает пространство всех возможных значений объекта ${ displaystyle p}$ , а затемненная область, ${ Displaystyle P (s)}$ , представляет собой набор точек, удовлетворяющих условиям устойчивости. Радиус синего круга, показанного красным, - это радиус устойчивости.

Абстрактное определение

Формальное определение этого понятия варьируется в зависимости от области применения. Следующее абстрактное определение весьма полезно^[1]^[2]

{ displaystyle { hat { rho}} ({ hat {p}}): = max { rho geq 0: p in P (s), forall p in B ( rho , { hat {p}}) }}

куда ${ displaystyle B ( rho, { hat {p}})}$ обозначает закрытый мяч радиуса ${ displaystyle rho}$ в ${ displaystyle P}$ сосредоточен на ${ displaystyle { hat {p}}}$ .

История

Похоже, концепция была изобретена в начале 1960-х годов.^[3]^[4] В 1980-х годах он стал популярным в теории управления.^[5] и оптимизация.^[6] Он широко используется в качестве модели локальной устойчивости к небольшим отклонениям от заданной номинальной стоимости интересующего объекта.

Связь с моделью максимина Вальда

Было показано^[2] что модель радиуса устойчивости является примером Модель максимина Вальда. Это,

{ displaystyle max { rho geq 0: p in P (s), forall p in B ( rho, { hat {p}}) } Equiv max _ { rho geq 0} min _ {p in B ( rho, { hat {p}})} f ( rho, p)}

куда

{ Displaystyle е ( rho, p) = left {{ begin {array} {cc} rho &, p in P (s) - infty &, p notin P (s ) end {array}} right.}

Большой штраф ( ${ displaystyle - infty}$ ) - это устройство, заставляющее ${ displaystyle max}$ игрок не нарушает номинал за пределами радиуса устойчивости системы. Это показатель того, что модель устойчивости является моделью локальной стабильности / устойчивости, а не глобальной.

Теория принятия решений по информационным пробелам

Теория принятия решений по информационным пробелам это недавняя теория вероятностных решений. Утверждается, что он радикально отличается от всех современных теорий принятия решений в условиях неопределенности. Но это было показано^[2] что его модель устойчивости, а именно

{ displaystyle { hat { alpha}} (q, { тильда {u}}): = max { alpha geq 0: r_ {c} leq R (q, u), forall и в U ( alpha, { tilde {u}}) }}

фактически является моделью радиуса устойчивости, характеризуемой простым требованием устойчивости вида ${ displaystyle r_ {c} leq R (q, u)}$ куда ${ displaystyle q}$ обозначает рассматриваемое решение, ${ displaystyle u}$ обозначает интересующий параметр, ${ displaystyle { tilde {u}}}$ обозначает оценку истинного значения ${ displaystyle u}$ и ${ Displaystyle U ( альфа, { тильда {и}})}$ обозначает шар радиуса ${ displaystyle alpha}$ сосредоточен на ${ displaystyle { tilde {u}}}$ .

Поскольку модели радиуса устойчивости предназначены для работы с небольшими отклонениями номинального значения параметра, модель устойчивости информационного зазора измеряет местная устойчивость решений в окрестности оценки ${ displaystyle { tilde {u}}}$ .

Сниедович^[2] утверждает, что по этой причине теория не подходит для обработки серьезной неопределенности, характеризующейся плохой оценкой и обширным пространством неопределенности.

Альтернативное определение

Бывают случаи, когда удобнее определять радиус устойчивости несколько иначе. Например, во многих приложениях в теории управления радиус устойчивости определяется как величина наименьшего дестабилизирующего возмущения номинального значения интересующего параметра.^[7] Картина такая:

Более формально

{ displaystyle { hat { rho}} (q): = min _ {p notin P (s)} dist (p, { hat {p}})}

куда ${ displaystyle dist (p, { hat {p}})}$ обозначает расстояние из ${ displaystyle p in P}$ из ${ displaystyle { hat {p}}}$ .

Радиус устойчивости функций

В радиус устойчивости из непрерывная функция ж (в функциональное пространство F) относительно открыто область стабильности D это расстояние между ж и набор неустойчивых функций (относительно D). Мы говорим, что функция стабильный относительно D если его спектр находится в D. Здесь понятие спектра определяется в каждом конкретном случае, как объясняется ниже.

Определение

Формально, если обозначить множество стабильных функций через S (D) а радиус устойчивости - на г (ж, D), тогда:

{ Displaystyle г (е, D) = inf _ {г в C} { | г |: е + г notin S (D) },}

куда C это подмножество F.

Обратите внимание, что если ж уже нестабильно (относительно D), тогда г (е, D) = 0 (так долго как C содержит ноль).

Приложения

Понятие радиуса устойчивости обычно применяется к специальные функции так как многочлены (тогда спектр - это корни) и матрицы (спектр - это собственные значения ). Случай, когда C является собственным подмножеством F позволяет рассматривать структурированные возмущения (например, для матрицы нам могут понадобиться возмущения только в последней строке). Это интересный показатель надежности, например, в теория управления.

Характеристики

Позволять ж быть (сложный ) полином степени п, C = F - множество полиномов степени меньше (или равной) п (которое мы здесь отождествляем с множеством ${ Displaystyle mathbb {C} ^ {п + 1}}$ коэффициентов). Мы принимаем за D Открыто единичный диск, что означает, что мы ищем расстояние между многочленом и множеством Шура стабильные многочлены. Потом:

{ Displaystyle г (е, D) = inf _ {z in partial D} { frac {| f (z) |} { | q (z) |}},}

куда q содержит каждый базисный вектор (например, ${ Displaystyle д (г) = (1, г, ldots, г ^ {п})}$ когда q - обычная силовая основа). Этот результат означает, что радиус устойчивости ограничен минимальным значением, которое ж достигает единичного круга.

Примеры

Полином ${ displaystyle f (z) = z ^ {8} -9/10}$ (нули которого являются корнями 8-й степени из 0.9) имеет радиус устойчивости 1/80, если q является степенным базисом, а норма - бесконечной нормой. Значит, должен существовать полином грамм с (бесконечной) нормой 1/90 такая, что ж + г имеет (по крайней мере) корень на единичной окружности. Такой грамм например ${ Displaystyle г (г) = - 1/90 сумма _ {я = 0} ^ {8} г ^ {я}}$ . В самом деле, (f + g) (1) = 0 и 1 находится на единичной окружности, что означает, что ж + г нестабильно.