Тетраэдрический купол - Tetrahedral cupola
| Тетраэдрический купол | ||
|---|---|---|
 Диаграмма Шлегеля | ||
| Тип | Многогранный купол | |
| Символ Шлефли | {3,3} v rr {3,3} | |
| Клетки | 16 | 1 рр {3,3} 1+4 {3,3} 4+6 {}×{3} |
| Лица | 42 | 24 треугольника 18 квадратов |
| Края | 42 | |
| Вершины | 16 | |
| Двойной | ||
| Группа симметрии | [3,3,1], порядок 24 | |
| Характеристики | выпуклый, правильное лицо | |
В 4-х мерном геометрия, то четырехгранный купол это полихорон ограничен одним тетраэдр, параллельный кубооктаэдр, соединенных 10 треугольные призмы, и 4 треугольные пирамиды.[1]
Связанные многогранники
В четырехгранный купол можно отрезать от 5-клеточный, на гиперплоскость параллельно тетраэдрической ячейке. В кубооктаэдр основание проходит через центр бегущей 5-ячеек, поэтому Тетраэдрический купол содержит половину тетраэдрических и треугольных призматических ячеек бегущей 5-ячейки. Купол можно увидеть на А2 и А3 Ортогональная проекция плоскости Кокстера 5-клеточной структуры:
| А3 Самолет Кокстера | ||
|---|---|---|
| Ранцинированный 5-клеточный | Тетраэдр (Верх купола) | Кубооктаэдр (Купольная база) |
 |  | 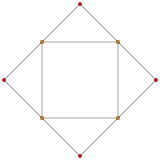 |
| А2 Самолет Кокстера | ||
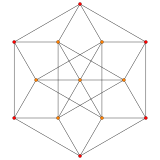 |  | 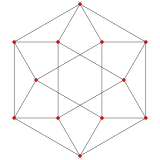 |
Смотрите также
- Тетраэдрическая пирамида (5 ячеек)
Рекомендации
- ^ Выпуклый сегментохора Д-р Ричард Клитцинг, Симметрия: культура и наука, Vol. 11, №№ 1-4, 139-181, 2000 (4,23 тетраэдр || кубооктаэдр)
внешняя ссылка
| Этот 4-многогранник статья - это заглушка. Вы можете помочь Википедии расширяя это. |
