Турбо код - Turbo code

В теория информации, турбокоды (первоначально на французском Турбокоды) являются классом высокопроизводительных упреждающее исправление ошибок (FEC) коды, разработанные в период с 1990 по 1991 год, но впервые опубликованные в 1993 году. Они были первыми практическими кодами, которые приблизились к максимальной пропускной способности канала или Предел Шеннона, теоретический максимум для кодовая скорость при котором надежная связь все еще возможна при определенном уровне шума. Турбокоды используются в 3G /4G мобильная связь (например, в UMTS и LTE ) И в (Глубокий космос ) спутник коммуникации а также другие приложения, в которых разработчики стремятся обеспечить надежную передачу информации по каналам связи с ограниченной полосой пропускания или задержкой при наличии искажающего данные шума. Турбо-коды конкурируют с Коды LDPC («проверка четности с низкой плотностью»), которые обеспечивают аналогичную производительность.

Название «турбо-код» возникло из-за контура обратной связи, используемого во время обычного декодирования турбокода, который был аналогичен обратной связи выхлопных газов, используемой для двигателя. турбонаддув. Hagenauer утверждал, что термин турбо-код является неправильным, поскольку в процессе кодирования нет обратной связи.^[1]

История

Заявка на фундаментальный патент на турбокоды была подана 23 апреля 1991 г. В патентной заявке перечислены Клод Берру как единственный изобретатель турбокодов. Подача патента привела к получению нескольких патентов, в том числе Патент США 5,446,747, срок действия которого истек 29 августа 2013 года.

Первой публичной статьей по турбо-кодам была "Кодирование и декодирование с исправлением ошибок, близкое к пределу Шеннона: турбо-коды".^[2] Этот документ был опубликован в 1993 г. в материалах Международной конференции по коммуникациям IEEE. Документ 1993 года был сформирован из трех отдельных документов, которые были объединены из-за нехватки места. В результате слияния газета перечислила трех авторов: Берроу, Glavieux, и Thitimajshima (от Télécom Bretagne, бывшего ENST Бретань, Франция). Однако из первоначальной заявки на патент ясно, что Берроу является единственным изобретателем турбо-кодов и что другие авторы статьи предоставили материал, отличный от основных концепций.

Турбокоды были настолько революционными на момент своего появления, что многие эксперты в области кодирования не поверили полученным результатам. Когда производительность была подтверждена, в мире кодирования произошла небольшая революция, которая привела к исследованию многих других типов итеративной обработки сигналов.

Первым классом турбокода был параллельный каскадный сверточный код (PCCC). С момента появления оригинальных параллельных турбокодов в 1993 году было обнаружено множество других классов турбокодов, включая серийные версии. последовательные конкатенированные сверточные коды и коды повторного накопления. Методы итеративного турбодекодирования также применялись к более традиционным системам FEC, включая сверточные коды с коррекцией Рида-Соломона, хотя эти системы слишком сложны для практической реализации итерационных декодеров. Турбо-эквализация также вытекала из концепции турбо-кодирования.

В дополнение к турбокодам Берроу также изобрел рекурсивные систематические сверточные коды (RSC), которые используются в примерной реализации турбокодов, описанных в патенте. Турбокоды, которые используют коды RSC, кажутся более эффективными, чем турбокоды, которые не используют коды RSC.

До турбокодов лучшие конструкции были серийными. составные коды на основе внешнего Исправление ошибок Рида-Соломона код в сочетании с внутренним Витерби-декодированный короткая длина ограничения сверточный код, также известные как коды RSV.

В более поздней статье Берроу отнесся к интуиции «Дж. Баттейла, Дж. Хагенауэр и П. Хоэхер, который в конце 80-х подчеркнул интерес к вероятностной обработке. "Он добавляет".Р. Галлагер и М. Таннер уже придумал методы кодирования и декодирования, общие принципы которых тесно связаны, «хотя необходимые вычисления в то время были непрактичными.^[3]

Пример кодировщика

Существует множество различных экземпляров турбокодов, использующих различные кодирующие компоненты, соотношения ввода / вывода, перемежители и шаблоны прокалывания. Этот пример реализации кодера описывает классический турбокодер и демонстрирует общую конструкцию параллельных турбокодов.

Эта реализация кодировщика отправляет три подблока битов. Первый подблок - это м-битовый блок данных полезной нагрузки. Второй подблок п / 2 биты четности для данных полезной нагрузки, вычисленные с использованием рекурсивного систематического сверточный код (Код RSC). Третий подблок - п / 2 биты четности для известного перестановка данных полезной нагрузки, снова вычисленных с использованием кода RSC. Таким образом, с полезной нагрузкой отправляются два избыточных, но разных подблока битов четности. Полный блок имеет м + п биты данных с кодовой скоростью м/(м + п). В перестановка данных полезной нагрузки выполняется устройством, называемым перемежитель.

Аппаратно этот турбокодер состоит из двух одинаковых кодеров RSC, С₁ и C₂, как показано на рисунке, которые соединены друг с другом с помощью схемы конкатенации, называемые параллельная конкатенация:

На рисунке M это регистр памяти. Входные биты линии задержки и силы перемежителя d_k появляться в разных последовательностях. На первой итерации входная последовательность d_k появляется на обоих выходах энкодера, Икс_k и у_1к или же у_2k из-за систематичности кодировщика. Если кодировщики C₁ и C₂ используются в п₁ и п₂ итераций, их скорости соответственно равны

${ displaystyle { begin {align} ~ R_ {1} & = { frac {n_ {1} + n_ {2}} {2n_ {1} + n_ {2}}} ~ R_ {2} & = { frac {n_ {1} + n_ {2}} {n_ {1} + 2n_ {2}}} end {выровнено}}}$

Декодер

Декодер построен аналогично вышеуказанному кодировщику. Два элементарных декодера соединены между собой, но последовательно, а не параллельно. В ${ displaystyle textstyle DEC_ {1}}$ декодер работает на более низкой скорости (т.е. ${ displaystyle textstyle R_ {1}}$), таким образом, он предназначен для ${ displaystyle textstyle C_ {1}}$ кодировщик и ${ displaystyle textstyle DEC_ {2}}$ это для ${ displaystyle textstyle C_ {2}}$ соответственно. ${ displaystyle textstyle DEC_ {1}}$ дает мягкое решение что приводит к ${ displaystyle textstyle L_ {1}}$ задерживать. Такая же задержка вызвана линией задержки в кодировщике. В ${ displaystyle textstyle DEC_ {2}}$причины операции ${ displaystyle textstyle L_ {2}}$ задерживать.

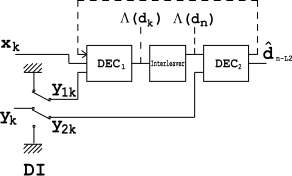
Перемежитель, установленный между двумя декодерами, используется здесь для рассеивания пакетов ошибок, исходящих от ${ displaystyle textstyle DEC_ {1}}$ выход. DI block - это модуль демультиплексирования и вставки. Он работает как переключатель, перенаправляя входные биты на ${ displaystyle textstyle DEC_ {1}}$ в один момент и чтобы ${ displaystyle textstyle DEC_ {2}}$ в другом. В выключенном состоянии он питает оба ${ displaystyle textstyle y_ {1k}}$ и ${ displaystyle textstyle y_ {2k}}$ входы с битами заполнения (нулями).

Считайте без памяти AWGN канал, и предположим, что при k-й итерации декодер получает пару случайных величин:

${ displaystyle { begin {align} ~ x_ {k} & = (2d_ {k} -1) + a_ {k} ~ y_ {k} & = 2 (Y_ {k} -1) + b_ { к} конец {выровнено}}}$

куда ${ displaystyle textstyle a_ {k}}$ и ${ displaystyle textstyle b_ {k}}$ независимые компоненты шума, имеющие одинаковую дисперсию ${ displaystyle textstyle sigma ^ {2}}$. ${ displaystyle textstyle Y_ {k}}$ это k-й бит от ${ displaystyle textstyle y_ {k}}$ выход энкодера.

Избыточная информация демультиплексируется и отправляется через DI к ${ displaystyle textstyle DEC_ {1}}$ (когда ${ displaystyle textstyle y_ {k} = y_ {1k}}$) и ${ displaystyle textstyle DEC_ {2}}$ (когда ${ displaystyle textstyle y_ {k} = y_ {2k}}$).

${ displaystyle textstyle DEC_ {1}}$ дает мягкое решение; то есть:

${ displaystyle Lambda (d_ {k}) = log { frac {p (d_ {k} = 1)} {p (d_ {k} = 0)}}}$

и доставляет его ${ displaystyle textstyle DEC_ {2}}$. ${ displaystyle textstyle Lambda (d_ {k})}$ называется логарифм отношения правдоподобия (LLR). ${ displaystyle textstyle p (d_ {k} = i), , i in {0,1 }}$ это апостериорная вероятность (APP) ${ displaystyle textstyle d_ {k}}$ бит данных, который показывает вероятность интерпретации полученного ${ displaystyle textstyle d_ {k}}$ немного как ${ displaystyle textstyle i}$. Принимая LLR в учетную запись, ${ displaystyle textstyle DEC_ {2}}$ дает трудное решение; то есть декодированный бит.

Известно, что Алгоритм Витерби не может рассчитать приложение, поэтому его нельзя использовать в ${ displaystyle textstyle DEC_ {1}}$. Вместо этого модифицированный Алгоритм BCJR используется. За ${ displaystyle textstyle DEC_ {2}}$, то Алгоритм Витерби подходящий.

Однако изображенная структура не является оптимальной, поскольку ${ displaystyle textstyle DEC_ {1}}$ использует только надлежащую часть доступной избыточной информации. Для улучшения конструкции используется петля обратной связи (см. Пунктирную линию на рисунке).

Подход мягких решений

Интерфейс декодера выдает целое число для каждого бита в потоке данных. Это целое число является мерой того, насколько вероятно, что бит равен 0 или 1, и также называется мягкий бит. Целое число может быть взято из диапазона [-127, 127], где:

• −127 означает «конечно 0»
• −100 означает «очень вероятно 0»
• 0 означает «это может быть либо 0, либо 1»
• 100 означает "очень вероятно 1"
• 127 означает "конечно 1"

Это вводит вероятностный аспект в поток данных от внешнего интерфейса, но он передает больше информации о каждом бите, чем просто 0 или 1.

Например, для каждого бита внешний интерфейс традиционного беспроводного приемника должен решить, находится ли внутреннее аналоговое напряжение выше или ниже заданного порогового уровня напряжения. Для декодера турбокода внешний интерфейс будет обеспечивать целочисленную меру того, насколько далеко внутреннее напряжение от заданного порога.

Чтобы расшифровать м + п-битовый блок данных, интерфейс декодера создает блок мер правдоподобия с одной мерой правдоподобия для каждого бита в потоке данных. Есть два параллельных декодера, по одному для каждого из^п⁄₂субблоки -битной четности. Оба декодера используют подблок м вероятности для данных полезной нагрузки. Декодер, работающий над вторым субблоком четности, знает перестановку, которую кодер использовал для этого субблока.

Решение гипотез для поиска битов

Ключевым нововведением турбокодов является то, как они используют данные вероятности для согласования различий между двумя декодерами. Каждый из двух сверточных декодеров генерирует гипотезу (с производными вероятностями) для шаблона м биты в подблоке полезной нагрузки. Битовые комбинации гипотез сравниваются, и, если они отличаются, декодеры обмениваются полученными вероятностями, которые они имеют для каждого бита в гипотезах. Каждый декодер включает в себя оценки правдоподобия, полученные от другого декодера, чтобы сформировать новую гипотезу для битов в полезной нагрузке. Затем они сравнивают эти новые гипотезы. Этот итеративный процесс продолжается до тех пор, пока два декодера не придут к одной и той же гипотезе для м-битовый шаблон полезной нагрузки, обычно от 15 до 18 циклов.

Можно провести аналогию между этим процессом и решением таких головоломок, как кроссворд или же судоку. Рассмотрим частично завершенный, возможно, искаженный кроссворд. Два решателя головоломки (декодера) пытаются решить эту задачу: у одного есть только «нисходящие» ключи (биты четности), а у другого - только «поперечные» ключи. Для начала оба решателя угадывают ответы (гипотезы) на свои подсказки, отмечая, насколько они уверены в каждой букве (бит полезной нагрузки). Затем они сравнивают записи, обмениваясь ответами и рейтингами доверия друг с другом, замечая, где и чем они отличаются. Основываясь на этих новых знаниях, они оба придумывают обновленные ответы и рейтинги уверенности, повторяя весь процесс, пока не придут к одному и тому же решению.

Спектакль

Турбокоды работают хорошо благодаря привлекательной комбинации случайного появления кода в канале вместе с физически реализуемой структурой декодирования. На турбо-коды влияет этаж ошибок.

Практические приложения с использованием турбокодов

Телекоммуникации:

• Турбокоды широко используются в 3G и 4G стандарты мобильной телефонии; например, в HSPA, EV-DO и LTE.
• MediaFLO, система наземного мобильного телевидения от Qualcomm.
• В канал взаимодействия из спутниковая связь системы, такие как DVB-RCS^[4] и DVB-RCS2.
• Недавний НАСА миссии, такие как Марсианский разведывательный орбитальный аппарат использовать турбо-коды как альтернативу RS -Витерби коды.
• IEEE 802.16 (WiMAX ), стандарт беспроводной городской сети, использует блочное турбо-кодирование и сверточное турбо-кодирование.

Байесовская формулировка

Из искусственный интеллект точки зрения, турбокоды можно рассматривать как пример зацикленного распространение веры в Байесовские сети.^[5]

Смотрите также

• Сверточный код
• Алгоритм Витерби
• Декодирование с мягким решением
• Перемежитель
• Алгоритм BCJR
• Код проверки на четность с низкой плотностью
• Последовательные каскадные сверточные коды
• Турбо эквалайзер
• Прямое исправление ошибок

Рекомендации

внешняя ссылка

• "Завершение идеального кода", IEEE Spectrum, март 2004 г.
• «Турбо-код UMTS и эффективная реализация декодера, подходящая для программно-определяемых радиостанций» (Международный журнал беспроводных информационных сетей)
• Дана Маккензи (2005), «Доведи до предела», Новый ученый, 187 (2507): 38–41, ISSN  0262-4079. (предварительный просмотр, копировать )
• «Нажимая предел», а Новости науки статья о развитии и генезисе турбокодов
• Международный симпозиум по турбо-кодам
• Библиотека кодированной модуляции, библиотека с открытым исходным кодом для моделирования турбо-кодов в Matlab
• «Турбо-уравнение: принципы и новые результаты», Транзакции IEEE по коммуникациям статья об использовании сверточных кодов совместно с канальной коррекцией.
• Домашняя страница IT ++ В IT ++ это мощная библиотека C ++, которая, в частности, поддерживает турбо-коды
• Публикации турбо-кодов Дэвида Маккея
• Домашняя страница AFF3CT (A Fast Forward Error Correction Toolbox) для моделирования высокоскоростных турбо-кодов в программном обеспечении
• Турбо код доктора Сильви Керуэдан и Доктор Клод Берру (scholarpedia.org).
• Эталонный дизайн 3GPP LTE Turbo.
• Оцените производительность BER турбокода в AWGN (MatLab).
• Параллельное каскадное сверточное кодирование: турбо-коды (MatLab Simulink)

дальнейшее чтение