Вириальное расширение - Virial expansion

Эта статья поднимает множество проблем. Пожалуйста помоги Улучши это или обсудите эти вопросы на страница обсуждения. (Узнайте, как и когда удалить эти сообщения-шаблоны) Эта статья возможно содержит оригинальные исследования. Пожалуйста Улучши это к проверка заявленные претензии и добавление встроенные цитаты. Заявления, содержащие только оригинальные исследования, следует удалить. (Июль 2019) (Узнайте, как и когда удалить этот шаблон сообщения) Эта статья может требовать уборка встретиться с Википедией стандарты качества. Конкретная проблема: Неформальный язык и ненейтральный тон Пожалуйста помоги улучшить эту статью если вы можете. (Июль 2019) (Узнайте, как и когда удалить этот шаблон сообщения) (Узнайте, как и когда удалить этот шаблон сообщения)

Классический вириальное расширение выражает давление ${ displaystyle P}$ из система многих частиц в равновесие как степенной ряд в числовая плотность:

${ Displaystyle Z Equiv { frac {P} {RT rho}} = A + B rho + C rho ^ {2} + cdots}$

Здесь количество ${ Displaystyle Z экв { гидроразрыва {P} {RT rho}}}$ это коэффициент сжимаемости. Это вириальное уравнение состояния, наиболее общая функция, связывающая PρT свойства жидкостей, впервые предложенная Камерлинг-Оннес.^[1] Коэффициент сжимаемости - это безразмерная величина, показывающая, насколько реальная жидкость отличается от идеального газа. А - это первый вириальный коэффициент, который имеет постоянное значение 1 и утверждает, что при низкой молярной плотности все жидкости ведут себя как идеальные газы. Вириальные коэффициенты B, C, Dи т. д., зависят от температуры и обычно представлены в виде ряда Тейлора через 1 /Т.

Второй и третий вириальные коэффициенты

Второй и третий вириальные коэффициенты интенсивно изучались и сводились в таблицы для многих жидкостей на протяжении более столетия. Наиболее обширный сборник был в книгах Димондса.^[2][3] Недавно Центр термодинамических исследований Национального института стандартов и технологий (NIST / TRC) опубликовал огромное количество термодинамических данных в виде веб-термо-таблиц (WTT).^[4] В версии WTT-Lite в Интернете доступны критически проверенные данные по 150 жидкостям. Таблицы второго и третьего вириальных коэффициентов многих жидкостей также включены в этот сборник.

2-й и 3-й вириальные коэффициенты аргона

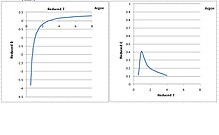
Второй и третий вириальные коэффициенты аргона как функции температуры показаны на следующем рисунке.^[5] Пониженная температура и пониженные вириальные коэффициенты, масштабируемые по соответствующим критическим свойствам, все безразмерны. Большинство жидкостей ведут себя одинаково.^{[когда определяется как? ]}

Второй вириальный коэффициент монотонно уменьшается с понижением температуры. Однако третий вириальный коэффициент имеет форму колокола. Он увеличивается при понижении температуры до критической, затем проходит через пик и быстро уменьшается до 0 при понижении температуры от критической точки до тройной точки. Физически неразумно, чтобы она уменьшалась ниже критической температуры, потому что третий вириальный коэффициент теоретически представляет силу отталкивания между тремя молекулами, которая, как ожидается, увеличится при более низкой температуре, поскольку молекулы сжимаются.

Причина уменьшения третьего вириального коэффициента ниже критической температуры заключается в том, что он был проанализирован неправильно. Обычно изотермы PρT удобно измерять в газовой фазе. Ниже критической температуры газовая фаза конденсируется и сосуществует с жидкой фазой, и изотерма PρT становится плоской. Давление насыщения не изменяется до тех пор, пока газ полностью не конденсируется в жидкость, а затем давление повышается по мере увеличения плотности. Существует большой разрыв между чистой газовой фазой и чистой жидкой фазой, где отсутствуют полезные данные о давлении, за исключением давления насыщения. Если анализировать только данные в газовой фазе, третий вириальный коэффициент становится очень малым, поскольку изотерма PρT в газовой фазе почти линейна. Однако, если бы были включены точки данных в чистой жидкой фазе, регрессия второго порядка дала бы большой третий вириальный коэффициент. Полученный таким образом третий вириальный коэффициент будет монотонно увеличиваться при понижении температуры от критической точки до тройной точки.

Ожидание того, что третий вириальный коэффициент является монотонно возрастающей функцией 1 / T, можно проверить с помощью уравнений состояния, которые точно предсказывают изотермы PρT в области насыщения, где сосуществуют газовая и жидкая фазы. Большинство уравнений состояния можно преобразовать в вириальную форму, так что полученные из них второй и третий вириальные коэффициенты можно будет точно сравнить.

Приведение уравнений состояния к вириальной форме

Большинство уравнений состояния можно переформулировать и преобразовать в вириальные уравнения, чтобы оценить и сравнить их неявные второй и третий вириальные коэффициенты. Основополагающий Уравнение Ван-дер-Ваальса государства,^[6] был предложен в 1873 г .:

${ displaystyle P = { frac {RT} { left (v-b right)}} - { frac {a} {v ^ {2}}}}$

куда v = 1/ρ молярный объем. Его можно переставить, расширив 1 / (v - б) в серию Тейлора:

${ displaystyle Z = 1 + left (b - { frac {a} {RT}} right) rho + b ^ {2} rho ^ {2} + b ^ {3} rho ^ {3 } + cdots}$

Второй вириальный коэффициент имеет примерно правильное поведение, поскольку он монотонно уменьшается при понижении температуры. Третий и более высокие вириальные коэффициенты не зависят от температуры и определенно неверны, особенно при низких температурах. Почти все последующие уравнения состояния, полученные из уравнения Ван-дер-Ваальса, как и уравнения Дитеричи,^[7] Бертело,^[8] Редлих-Квонг,^[9] Пенг-Робинсон,^[10] и т. д., страдали от особенности, вносимой 1 / (v - б), и невозможно было заставить точно представить изотермы PρT при температурах ниже критической. Многие из них дали адекватные вторые вириальные коэффициенты, но большинство дали неправильные третьи вириальные коэффициенты.

Другая школа уравнений состояния, начатая Битти-Бриджманом,^[11] тем не менее, они были более тесно связаны с вириальными уравнениями и показали более точное представление поведения флюидов как в газовой, так и в жидкой фазах. Их легко переформулировать в вириальные уравнения состояния и сравнить друг с другом. Уравнение состояния Битти-Бриджмена, предложенное в 1928 г.,

${ displaystyle p = { frac {RT} {v ^ {2}}} left (1 - { frac {c} {vT ^ {3}}} right) (v + B) - { frac {A} {v ^ {2}}}}$

куда

${ displaystyle A = A_ {0} left (1 - { frac {a} {v}} right)}$

${ displaystyle B = B_ {0} left (1 - { frac {b} {v}} right)}$

можно переставить:

${ displaystyle Z = 1 + left (B_ {0} - { frac {A_ {0}} {RT}} - { frac {c} {RT ^ {3}}} right) rho - left (B_ {0} b - { frac {A_ {0} a} {RT ^ {3}}} right) rho ^ {2} + left ({ frac {B_ {0} bc} { T ^ {3}}} right) rho ^ {3}}$

Это уравнение состояния очень хорошо отражает второй вириальный коэффициент. Однако третий вириальный коэффициент имел неправильный знак. Следовательно, он не смог представить изотермы, близкие к критической температуре и ниже нее.

Уравнение состояния Бенедикта-Вебба-Рубина^[12] в 1940 г. произошло значительное улучшение в представлении изотерм ниже критической температуры:

${ displaystyle Z = 1 + left (B_ {0} - { frac {A_ {0}} {RT}} - { frac {C_ {0}} {RT ^ {3}}} right) rho + left (b - { frac {a} {RT}} right) rho ^ {2} + left ({ frac { alpha a} {RT}} right) rho ^ {5 } + { frac {c rho ^ {2}} {RT ^ {3}}} left (1+ gamma rho ^ {2} right) exp left (- gamma rho ^ { 2} right)}$

Другие улучшения были предложены Starling^[13] в 1972 г .:

${ displaystyle Z = 1 + left (B_ {0} - { frac {A_ {0}} {RT}} - { frac {C_ {0}} {RT ^ {3}}} + { frac {D_ {0}} {RT ^ {4}}} - { frac {E_ {0}} {RT ^ {5}}} right) rho + left (b - { frac {a} { RT}} - { frac {d} {RT ^ {2}}} right) rho ^ {2} + alpha left ({ frac {a} {RT}} + { frac {d} {RT ^ {2}}} right) rho ^ {5} + { frac {c rho ^ {2}} {RT ^ {3}}} left (1+ gamma rho ^ {2 } right) exp left (- gamma rho ^ {2} right)}$

Ниже приведены графики уменьшенных второго и третьего вириальных коэффициентов в зависимости от пониженной температуры согласно Старлингу [13]:

2-й и 3-й вириальные коэффициенты для 12 флюидов.

Экспоненциальные члены в последних двух уравнениях кажутся устрашающими и неприемлемыми для последовательности вириального разложения. Его цель состояла в том, чтобы исправить третий вириальный коэффициент, чтобы изотермы в жидкой фазе могли быть правильно представлены. На самом деле экспоненциальный член очень быстро сходится как ρ увеличивается, и если мы возьмем только первые два члена в его ряду разложения Тейлора, ${ displaystyle 1- gamma rho ^ {2}}$, и умножьте его на ${ displaystyle 1+ gamma rho ^ {2}}$, результат ${ Displaystyle 1- gamma ^ {2} rho ^ {4}}$. Таким образом, это способствовало ${ displaystyle c / RT ^ {3}}$ член третьего вириального коэффициента и один член восьмого вириального коэффициента, который можно эффективно игнорировать.

После разложения экспоненциальных членов уравнения состояния Бенедикта-Уэбба-Рубина и Старлинга имеют такую ​​интересную форму:

${ Displaystyle Z = 1 + b rho _ {r} + c rho _ {r} ^ {2} + f rho _ {r} ^ {5}}$

Четвертый и пятый вириальные коэффициенты равны нулю. После третьего вириального члена следующий значимый член - шестой вириальный коэффициент. Кажется, что первые три вириальных члена доминируют над коэффициентом сжимаемости жидкостей, вплоть до ${ displaystyle 0,5T_ {c}}$, и до ${ displaystyle 2.0 rho _ {c}}$.

В оригинальном исследовании 1901 года Камерлинг-Оннеса [1] он опустил четвертый вириальный коэффициент D, и обозначил высшие члены как остаток в своем вириальном уравнении. К сожалению, значение первых трех третьих вириальных членов так и не было полностью оценено, и их влияние на газо-жидкое равновесие было замаскировано другими более высокими вириальными коэффициентами в слепом поиске точности, с алгоритмами «многомерной оптимизации» и т.п. .

Теперь понятно, почему Бенедикт-Уэбб-Рубин улучшил уравнение состояния Битти-Бриджмена, добавив сложный экспоненциальный член. Они должны были признать, что третий вириальный коэффициент в газовой фазе мал, но должен быть большим в жидкой фазе. Вместо увеличения третьего вириального коэффициента они решили добавить странный экспоненциальный член, единственной целью которого было увеличение третьего вириального коэффициента при более низких температурах. Расширение Тейлора этого экспоненциального члена раскрывает их истинные намерения.

При повторном анализе данных, представленных Старлингом [13], лучше всего представлены вириальные коэффициенты:

${ displaystyle b = b_ {0} + { frac {b_ {1}} {t_ {r}}} + { frac {b_ {2}} {t_ {r} ^ {2}}} + { гидроразрыв {b_ {3}} {t_ {r} ^ {3}}}}$

${ displaystyle c = c_ {0} + { frac {c_ {1}} {t_ {r}}} + { frac {c_ {2}} {t_ {r} ^ {2}}} + { гидроразрыв {c_ {3}} {t_ {r} ^ {3}}}:}$

${ displaystyle f = f_ {0} + { frac {f_ {1}} {t_ {r}}}}$

b и c могут быть определены с использованием простого регрессионного анализа второго порядка из экспериментальных изотерм PρT. ${ displaystyle b_ {0} -b_ {3}}$ и ${ displaystyle c_ {0} -c_ {3}}$ затем можно определить с помощью регрессионного анализа третьего порядка на б и c. ${ displaystyle f_ {0} -f_ {1}}$ затем может быть определен путем анализа остатков в коэффициенте сжимаемости после удаления первых трех вириальных членов из вириального уравнения. Данные, представленные Старлингом [13], повторно анализируются, и результаты показаны в следующей таблице. Все эти коэффициенты безразмерны, поскольку все они масштабированы с учетом критических молярных объемов и критической температуры.

Жидкость	${ displaystyle b_ {0}}$	${ displaystyle b_ {1}}$	${ displaystyle b_ {2}}$	${ displaystyle b_ {3}}$	${ displaystyle c_ {0}}$	${ displaystyle c_ {1}}$	${ displaystyle c_ {2}}$	${ displaystyle c_ {3}}$	${ displaystyle f_ {0}}$	${ displaystyle f_ {1}}$
Метан	0.440	-1.171	-0.236	-0.210	0.364	-0.275	-0.014	0.396	0.0319	1.71E-03
Этан	0.330	-0.806	-0.363	-0.378	0.553	-0.675	-0.038	0.680	0.0461	2.63E-03
Пропан	0.288	-0.706	-0.245	-0.575	0.532	-0.546	-0.308	0.843	0.0334	1.89E-02
н-бутан	0.377	-0.916	-0.115	-0.610	0.547	-0.519	-0.347	0.871	0.0305	2.04E-02
и-бутан	0.438	-1.051	-0.172	-0.401	0.483	-0.342	-0.021	0.538	0.0194	1.19E-03
н-пентан	0.481	-1.056	-0.166	-0.560	0.668	-0.720	-0.204	0.841	0.0411	1.17E-02
и-пентан	0.242	-0.674	-0.306	-0.520	0.815	-0.943	-0.194	0.868	0.0484	9.99E-03
н-хин	0.435	-0.636	-0.358	-0.759	0.848	-1.275	-0.105	1.120	0.0604	4.98E-03
н-гептан	0.493	-0.798	-0.636	-0.428	0.589	-0.738	-0.017	0.814	0.0508	1.21E-03
н-октан	0.600	-0.744	-0.456	-0.763	0.174	-0.197	-0.272	0.919	0.0144	1.99E-02
Азот	0.502	-1.380	0.092	-0.333	0.400	-0.276	-0.027	0.322	0.0279	2,72E-03
CO2	0.178	-0.044	-1.517	0.039	0.428	-0.422	-0.008	0.687	0.0490	9.52E-04
ЧАС2S	0.191	-0.927	-0.078	-0.366	1.093	-1.227	-0.001	0.577	0.0578	8,37E-05

Кубическое вириальное уравнение состояния

Очень интересно, что трехчленное вириальное уравнение или кубическое вириальное уравнение состояния

${ Displaystyle Z = 1 + B rho + C rho ^ {2}}$

обладает всеми прекрасными атрибутами уравнения состояния Ван-дер-Ваальса без его фатальной сингулярности на v = б. Теоретически второй вириальный коэффициент представляет силы бимолекулярного притяжения, а третий вириальный член представляет силы отталкивания между тремя молекулами в тесном контакте. Интуитивно следует ожидать B стал отрицательным при низкой температуре, а C останется положительным, чтобы уравновесить эффект B и толкает Z и, следовательно, давление до высоких значений как ρ увеличивается.

Как упоминалось ранее, это кубическое вириальное уравнение состояния имеет все атрибуты уравнения состояния Ван-дер-Ваальса, без существенной проблемы сингулярности при v = б. В критическом состоянии коэффициенты B и C могут быть решены в близкой форме. Создание критических условий:

${ displaystyle { frac { mathrm {d} P} { mathrm {d} v}} = 0}$ и ${ displaystyle { frac { mathrm {d} ^ {2} P} { mathrm {d} v ^ {2}}} = 0}$

кубическое вириальное уравнение можно решить, чтобы получить:

${ displaystyle B = -v_ {c}}$ , ${ displaystyle C = { frac {v_ {c} ^ {2}} {3}}}$ и :${ displaystyle Z_ {c} = { frac {P_ {c} v_ {c}} {RT_ {c}}} = 1/3}$

${ displaystyle Z_ {c}}$ поэтому составляет 0,333 по сравнению с 0,375 из уравнения состояния Ван-дер-Ваальса.

Между критической точкой и тройной точкой находится область насыщения флюидов. В этой области газовая фаза сосуществует с жидкой фазой под давлением насыщения. ${ displaystyle P _ { rm {sat}}}$, и температура насыщения ${ displaystyle T _ { rm {sat}}}$. Под давлением насыщения жидкая фаза имеет молярный объем ${ displaystyle v _ { rm {l}}}$, а газовая фаза имеет молярный объем ${ displaystyle v _ { rm {g}}}$. Соответствующие молярные плотности равны ${ displaystyle rho _ { rm {l}}}$ и ${ displaystyle rho _ { rm {g}}}$. Это свойства насыщения, необходимые для вычисления второго и третьего вириальных коэффициентов.

Действительное уравнение состояния должно давать изотерму, пересекающую горизонтальную линию ${ displaystyle P _ { rm {sat}}}$ в ${ displaystyle v _ { rm {l}}}$ и ${ displaystyle v _ { rm {g}}}$, на ${ displaystyle T _ { rm {sat}}}$. Под ${ displaystyle P _ { rm {sat}}}$ и ${ displaystyle T _ { rm {sat}}}$, газ находится в равновесии с жидкостью. Это означает, что изотерма PρT должна иметь три корня при ${ displaystyle P _ { rm {sat}}}$. Кубическое вириальное уравнение состояния при ${ displaystyle T _ { rm {sat}}}$ является:

${ displaystyle P _ { rm {sat}} = RT _ { rm {sat}} left (1 + B rho + C rho ^ {2} right) rho}$

Его можно переставить так:

${ displaystyle 1 - { frac {RT _ { rm {sat}}} {P _ { rm {sat}}}} left (1 + B rho + C rho ^ {2} right) rho = 0}$

Фактор ${ displaystyle RT _ { rm {sat}} / P _ { rm {sat}}}$ фактически является объемом насыщенного газа в соответствии с законом идеального газа, и ему можно дать уникальное имя ${ displaystyle v ^ { rm {id}}}$:

${ displaystyle v ^ { rm {id}} = { frac {RT _ { rm {sat}}} {P _ { rm {sat}}}}}$

В области насыщения кубическое уравнение имеет три корня, и его можно альтернативно записать как:

${ displaystyle left (1-v _ { rm {l}} rho right) left (1-v _ { rm {m}} rho right) left (1-v _ { rm {g }} rho right) = 0}$

который может быть расширен как:

${ displaystyle 1- left (v _ { rm {l}} + v _ { rm {g}} + v_ {m} right) rho + left (v _ { rm {l}} v _ { rm {g}} + v _ { rm {g}} v _ { rm {m}} + v _ { rm {m}} v _ { rm {l}} right) rho ^ {2} -v_ { rm {l}} v _ { rm {g}} v _ { rm {m}} rho ^ {3} = 0}$

${ displaystyle v _ { rm {m}}}$ объем неустойчивого состояния между ${ displaystyle v _ { rm {l}}}$ и ${ displaystyle v _ { rm {g}}}$. Кубические уравнения идентичны. Следовательно, из линейных членов в этих уравнениях, ${ displaystyle v_ {m}}$ можно решить:

${ displaystyle v _ { rm {m}} = v ^ { rm {id}} - v _ { rm {l}} - v _ { rm {g}}}$

Из квадратичных членов B можно решить:

${ displaystyle B = - { frac { left (v _ { rm {l}} v _ { rm {g}} + v _ { rm {g}} v _ { rm {m}} + v _ { rm {m}} v _ { rm {l}} right)} {v ^ { rm {id}}}}}$

А в кубических условиях C можно решить:

${ displaystyle C = { frac {v _ { rm {l}} v _ { rm {g}} v _ { rm {m}}} {v ^ { rm {id}}}}}$

С ${ displaystyle v _ { rm {l}}}$, ${ displaystyle v _ { rm {g}}}$ и ${ displaystyle P _ { rm {sat}}}$ были составлены таблицы для многих жидкостей с ${ displaystyle T _ { rm {sat}}}$ в качестве параметра просто вычислить B и C в области насыщения этих жидкостей. Результаты в целом согласуются с результатами, вычисленными по уравнениям состояния Бенедикта-Уэбба-Рубина и Старлинга. Однако точность в B и C критически зависят от измерений ${ displaystyle v _ { rm {g}}}$ и ${ displaystyle P _ { rm {sat}}}$, которые очень сложно точно измерить при низких температурах. Таким образом, ошибки измерения, вносимые в B и C следует учитывать при сравнении полученных таким образом значений со значениями, полученными в результате регрессионного анализа изотерм PρT второго порядка.

Равновесие газ-жидкость-твердое тело

Кубическое вириальное уравнение состояния точно представляет газожидкостное равновесие большинства веществ от критической точки до тройной точки, где начинает появляться твердая фаза. Его несложно расширить для учета равновесия газ-жидкость-твердое тело:

${ displaystyle P = { frac {RT} {V}} left (1 + { frac {B} {V}} + { frac {C} {V ^ {2}}} + { frac { U} {V ^ {n}}} + { frac {W} {V ^ {2n}}} right)}$

В этом вириальном уравнении первый член ${ displaystyle { frac {RT} {V}}}$ представляет собой давление, создаваемое кинетической энергией молекул. Второй срок ${ displaystyle { frac {RTB} {V ^ {2}}}}$ представляет собой дальнодействующее бимолекулярное притяжение, а третий член ${ displaystyle { frac {RTC} {V ^ {3}}}}$ представляет собой трехмолекулярное отталкивание на коротком расстоянии. Второй член толкает изотерму PVT вниз по мере уменьшения объема, а третий член толкает изотерму вверх. Когда температура ниже критической точки, изотерма PVT, таким образом, имеет S-образный изгиб, который позволяет жидкой фазе сосуществовать с преобладающей газовой фазой.

Если бы у нас был ${ displaystyle { frac {RTU} {V ^ {n}}}}$ член для опускания изотермы PVT в жидкую фазу, и ${ displaystyle { frac {RTW} {V ^ {2n}}}}$ Чтобы подтолкнуть его обратно вверх, может быть создана твердая фаза, поскольку эти два элемента создают еще один S-образный изгиб между жидкостью и твердым телом. Было продемонстрировано ^[14] что такой S-образный изгиб может быть синтезирован с использованием ${ displaystyle delta}$-функция типа функции Лоренца над уравнением состояния Ван-дер-Ваальса. Такое уравнение состояния было некрасивым, и им очень трудно было манипулировать математически. Приведенное выше вириальное уравнение намного чище и проще.

Аргон используется для реалистичной оценки этого расширенного вириального уравнения для равновесия газ-жидкость-твердое тело. Данные будут проанализированы в сокращенных формах. Все переменные PVT масштабируются по их соответствующим критическим значениям. Из принципа соответствующих состояний ожидается, что результаты будут применимы к другим жидкостям с хорошими характеристиками. Соответствующие данные для аргона приведены в следующей таблице:

Когда переменные п, V, и Т заменяются их приведенными эквивалентами, ${ displaystyle p = { frac {P} {P_ {c}}}}$, ${ displaystyle v = { frac {V} {V_ {c}}}}$, и ${ displaystyle t = { frac {T} {T_ {c}}}}$, вириальное уравнение принимает следующий вид:

${ displaystyle p = { frac {t} {vZ_ {c}}} left (1 - { frac {b} {v}} + { frac {c} {v ^ {2}}} - left ({ frac {v_ {u}} {v}} right) ^ {n} + left ({ frac {v_ {w}} {v}} right) ^ {2n} right)}$

куда ${ displaystyle Z_ {c} = { frac {P_ {c} V_ {c}} {RT_ {c}}}}$, ${ displaystyle b = { frac {B} {V_ {c}}}}$, ${ displaystyle c = { frac {C} {V_ {c} ^ {2}}}}$, ${ Displaystyle U = v_ {u} ^ {n}}$, и ${ Displaystyle W = v_ {w} ^ {2n}}$. Нас будет интересовать в основном условие в тройной точке аргона, где б = 3,424 и c = 1,152 из более раннего исследования [ссылка отсутствует].

.

${ displaystyle V_ {w}}$ должен быть немного больше, чем объем твердого аргона, 0,33, и ${ displaystyle v_ {u}}$ должен находиться между объемами жидкого и твердого аргона. Первоначально, ${ displaystyle v_ {w}}$ устанавливается равным объему твердого вещества, чтобы получить последний резко нарастающий край изотермы, где твердая фаза появляется при очень малом объеме. Экспоненциальный п затем необходимо определить, чтобы долина в п-2п потенциал должен уместиться между объемами твердого (0,33) и жидкого (0,378). После определения экспоненты n значение ${ displaystyle v_ {u}}$ может быть скорректирован так, чтобы удовлетворять правилу Гиббса, которое требует, чтобы свободная энергия Гиббса жидкой и твердой фаз была равной при температуре и давлении тройной точки.

Чтобы получить твердую фазу в аргоне, экспоненциальное значение n должно быть очень большим, больше 20; в противном случае изотерма PVT не смогла бы принять S-образную форму между жидкостью и твердым телом. Лучшая оценка заключается в том, что п = 30, ${ displaystyle t_ {t} = 0,553}$, ${ displaystyle v_ {w} = 0,335}$, и ${ displaystyle v_ {u} = 0,3443}$. Изотерма показана на правом рисунке, на котором три вириальных члена нанесены отдельно для ясности:

${ displaystyle p_ {1} = { frac {t_ {t}} {vZ_ {c}}} left (1 - { frac {b} {v}} + { frac {c} {v ^ { 2}}} right)}$

${ displaystyle p_ {2} = { frac {t_ {t}} {vZ_ {c}}} left ({ frac {v_ {u}} {v}} right) ^ {n}}$

${ displaystyle p = { frac {t_ {t}} {vZ_ {c}}} left ({ frac {v_ {w}} {v}} right) ^ {2n}}$

${ displaystyle p = p_ {1} -p_ {2} + p_ {3}}$

PVT-изотерма аргона с n = 30.

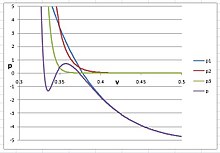
На этом рисунке ${ displaystyle p_ {1}}$ представляет собой сумму первых трех вириальных членов кубического вириального уравнения и показывает поведение аргона в его газовой и жидкой фазах. ${ displaystyle p_ {2}}$ представляет собой потенциал, внесенный ${ displaystyle left ({ frac {v_ {u}} {v}} right) ^ {n}}$ срок, и ${ displaystyle p_ {3}}$ представляет собой взносы ${ displaystyle left ({ frac {v_ {w}} {v}} right) ^ {2n}}$ срок. Когда п < 30, ${ displaystyle p_ {2}}$ будет мешать ${ displaystyle p_ {1}}$ и значительно снизить объем жидкости.

Было удивительно, что для образования твердой фазы n должно быть больше 20. Было хорошо известно, что потенциал Ленарда-Джонса 6-12 использовался для вычисления второго вириального коэффициента на основе принципов квантовой механики. Квантовая механика связывает второй вириальный коэффициент с бимолекулярным притяжением, а третий коэффициент с трехмолекулярным отталкиванием и т. Д. В жидкой фазе аргона один атом окружен 12 ближайшими соседями и до 32 ближайших соседей. . В твердой фазе все атомы заблокированы на месте, а количество взаимодействующих соседей бесконечно. Следовательно, п = 30 или даже больше, вполне разумно, хотя и удивительно.

Впервые в истории термодинамики у нас есть вириальное уравнение состояния для количественного описания равновесия газ-жидкость-твердое тело для аргона и всех жидкостей, которые соблюдают принцип соответствующих состояний в его тройной точке:

${ displaystyle p = { frac {t_ {t}} {vZ_ {c}}} left (1 - { frac {3.424} {v}} + { frac {1.152} {v ^ {2}}) } - left ({ frac {0.3443} {v}} right) ^ {30} + left ({ frac {0.3350} {v}} right) ^ {60} right)}$

Состояние вириальных уравнений

С развитием компьютеров вириальные уравнения использовались для представления больших объемов данных PρT без понимания их коэффициентов. Из уравнений состояния Бенедикта-Уэбба-Рубина и Старлинга было определено, что наилучшее вириальное уравнение состояния должно иметь форму:${ Displaystyle Z = 1 + b rho _ {r} + c rho _ {r} ^ {2} + f rho _ {r} ^ {5}}$. Второй и третий вириальные коэффициенты в этом уравнении можно вычислить из экспериментальных данных PρT с помощью простой линейной регрессии, доступной в Excel. После удаления первых трех вириальных членов остаток в коэффициенте сжимаемости Z затем будет проанализирован для получения шестого вириального коэффициента.

Смотрите также

• Теорема вириала
• Статистическая механика
• Уравнение состояния

Рекомендации