Граф Винера – Арайи - Wiener–Araya graph
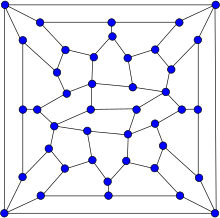
| Граф Винера-Арая | |
|---|---|
 | |
| Вершины | 42 |
| Края | 67 |
| Радиус | 5 |
| Диаметр | 7 |
| Обхват | 4 |
| Автоморфизмы | 2 |
| Хроматическое число | 3 |
| Хроматический индекс | 4 |
| Характеристики | Гипогамильтониан Планарный |
| Таблица графиков и параметров | |
В Граф Винера – Арайи в теория графов, граф на 42 вершинах с 67 ребрами. это гипогамильтониан, что означает, что он сам не имеет Гамильтонов цикл но каждый граф, образованный удалением из него единственной вершины, является Гамильтониан. Это также планарный.
История
Гипогамильтоновы графы были впервые изучены Сусселье в Problèmes plaisantset délectables (1963).[1]В 1967 году Линдгрен строит бесконечную последовательность гипогамильтоновых графов.[2]Он сначала цитирует Годена, Герца и Росси,[3] затем Бусакер и Саати[4]как пионеры в этой теме.
С самого начала самый маленький гипогамильтонов граф известно: Граф Петерсена. Однако охота на самых маленьких планарный гипогамильтонов граф продолжается. Этот вопрос впервые был задан Вацлав Хваталь в 1973 г.[5]Ответ дал в 1976 г. Карстен Томассен, который демонстрирует 105-вершинную конструкцию, 105-Томассен график.[6]В 1979 году Хацель улучшил этот результат, добавив планарный гипогамильтонов граф на 57 вершинах: Граф Хацеля.[7]В 2007 г. этот предел был понижен 48-график Замфиреску.[8]
В 2009 году граф, построенный Габором Винером и Макото Арайей, становится (с его 42 вершинами) самым маленьким планарный гипогамильтонов граф известен.[9][10]В своей статье Винер и Арая предполагают, что их граф является оптимальным, утверждая, что его порядок (42 ) кажется ответ на главный вопрос жизни, Вселенной и всего остального из Автостопом по Галактике, а Дуглас Адамс Роман.
Рекомендации
- ^ Сусселье, Р. (1963), Проблем нет. 29: Le cercle des irascibles, 7, Rev. Franç. Речь. Opérationnelle, стр. 405–406.
- ^ Линдгрен, В. Ф. (1967), "Бесконечный класс гипогамильтоновых графов", Американский математический ежемесячный журнал, 74: 1087–1089, Дои:10.2307/2313617, МИСТЕР 0224501
- ^ Gaudin, T .; Herz, P .; Росси (1964), "Решение проблемы № 29", Преподобный Franç. Речь. Операционнель (На французском), 8: 214–218
- ^ Busacker, R.G .; Саати, Т. Л. (1965), Конечные графы и сети
- ^ Хватал, В. (1973), «Триггеры в гипогамильтоновых графах», Канадский математический бюллетень, 16: 33–41, Дои:10.4153 / cmb-1973-008-9, МИСТЕР 0371722
- ^ Томассен, Карстен (1976), "Плоские и бесконечные гипогамильтоновы и отслеживаемые графы", Дискретная математика, 14 (4): 377–389, Дои:10.1016 / 0012-365x (76) 90071-6, МИСТЕР 0422086
- ^ Hatzel, Вольфганг (1979), "Ein planarer hypohamiltonscher Graph mit 57 Knoten", Mathematische Annalen (на немецком), 243 (3): 213–216, Дои:10.1007 / BF01424541, МИСТЕР 0548801
- ^ Zamfirescu, Кэрол Т .; Замфиреску, Тюдор И. (2007), "Планарный гипогамильтонов граф с 48 вершинами", Журнал теории графов, 55 (4): 338–342, Дои:10.1002 / jgt.20241, МИСТЕР 2336805
- ^ Винер, Габор; Арая, Макото (20 апреля 2009 г.), Главный вопрос, arXiv:0904.3012, Bibcode:2009arXiv0904.3012W.
- ^ Винер, Габор; Арая, Макото (2011), "О планарных гипогамильтоновых графах", Журнал теории графов, 67 (1): 55–68, Дои:10.1002 / jgt.20513, МИСТЕР 2809563.
