Участок Зисмана - Zisman Plot
В Зисман сюжет графический метод Теория Зисмана или Метод Зисмана для характеристики смачиваемости твердой поверхности [1], названный в честь американского химика и геофизика, Уильям Альберт Зисман (1905–1986). Это видный Техника Sessile drop используется для характеристики взаимодействия жидкости с поверхностью на основе угол контакта одной капли жидкости, сидящей на твердой поверхности.
Участок Зисмана
В 1964 г. Уильям Зисман опубликовал статью в публикациях ACS на тему «Связь равновесного краевого угла смачивания жидкости и твердого тела».[1] Именно в этой статье он использовал то, что мы сегодня называем сюжетом Зисмана. График Зисмана используется для очень быстрого количественного измерения смачиваемости, также известного как критическое поверхностное натяжение, γC , твердой поверхности путем измерения жидкости угол контакта как показано на рисунке 1. Взяв косинус указанного угла и затем построив его график относительно поверхностное натяжение жидкости, смачивающей твердую подложку, дает критическое поверхностное натяжение. Смачиваемость - это мера того, насколько хорошо жидкость растекается и насколько полный контакт жидкости по поверхности твердой поверхности раздела. Небольшой контактный угол указывает на хорошую смачиваемость, тогда как большой контактный угол указывает на плохую смачиваемость. Критическое поверхностное натяжение - это максимальное поверхностное натяжение жидкости, которое может полностью смачивать определенную твердую поверхность. Для склеивания используется полное смачивание, чтобы максимизировать прочность клеевого шва.
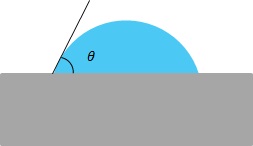
Рисунок 1: Схема измеренного угла смачивания жидкости на твердой подложке. Где θ - контактный угол, обозначаемый также в этом случае θSL.
Несмотря на то, что это соотношение является эмпирическим и менее точным, чем поверхностное натяжение гомологического ряда жидкостей, оно очень полезно, учитывая, что это параметр твердой поверхности. Этот метод особенно используется для быстрого и простого сравнения и измерения критического поверхностного натяжения твердых тел с низким энергопотреблением (в основном пластмасс). Рисунок 4 в опубликованной статье ЗИсмана за 1964 год.[1] показывает критическое поверхностное натяжение как меру смачиваемости полиэтилена. Зисман опубликовал этот анализ в 1964 году и использовал множество негомологичных жидкостей для измерения критического поверхностного натяжения полиэтилена, которое составило около 35 дин на сантиметр, как показано точкой пересечения при x = 1 на рисунке 4. Рисунок 12 в статье Зисмана 1964 года.[1] показывает, что различные твердые тела также могут быть нанесены на один и тот же график, чтобы легко сравнить критическое поверхностное натяжение твердых тел различных пластиковых подложек, включая очень разные полимеры, такие как тефлон, кислотные монослои и сложные эфиры. График Зисмана оказался прорывом, позволившим создать очень эффективный способ измерения смачиваемости твердого тела, что послужило началом работы Данна в конце 1960-х годов.[2] Данн охарактеризовал критическое поверхностное натяжение различных полимерных материалов, используя график Зисмана. В наши дни Дэвид и Нойман изучают краевой угол смачивания на низкоэнергетических поверхностях.[3] Однако сегодня существуют различные вариации графика Зисмана, потому что зависимая переменная не имеет единицы измерения, поскольку она является косинусом краевого угла смачивания для жидкости.
Современные варианты сюжета Зисмана
Для склеивания материалов смачивание поверхности, которое можно измерить по краю контакта, имеет решающее значение для успешного нанесения клея. Чтобы определить, насколько хорошо жидкость смачивает твердую поверхность, необходимо определить угол контакта с жидкостью на твердом теле. Это определяется соответствующим поверхностным натяжением твердого тела и жидкости. Вклад Уильяма Зисмана в адгезивы в виде его графика Зисмана, который сегодня имеет разновидность, которая отображает 1-cos (θSL) против γL . В этом варианте пересечение по оси X дает критическое поверхностное натяжение жидкости, необходимое для эффективного смачивания твердой поверхности. При построении графика данных есть два шага: пренебречь всеми точками вокруг нуля на оси Y, чтобы сначала построить линию наилучшего соответствия для нахождения γ.c ; однако при начальном построении линии, если точка около 0 приземляется справа от пересечения, повторите регрессию, включая эту точку, чтобы произвести измерение критического поверхностного натяжения, γc, более точным. Таблицу переменных и пример можно увидеть ниже.
Таблица переменных
| Переменная | Описание | Единицы |
|---|---|---|
| θSL | Угол падения капли жидкости на твердое тело, как показано на рисунке 1 | градусы или радианы |
| 1-cos (θSL) | Ось Y графика Зисмана представляет увлажнение | безразмерный |
| γL | Поверхностное натяжение соответствующей жидкости | дин / см |
| γC | Критическое поверхностное натяжение жидкости, необходимое для эффективного смачивания твердой основы. | дин / см |
пример
В этом примере мы будем использовать пять жидкостей в таблице 2 (данные о жидкости), чтобы найти критическое поверхностное натяжение смачивания, необходимое для эффективного смачивания ПК (поликарбоната), используя график Зисмана.
| Жидкое число | (Ось X) Поверхностное натяжение (дин / см) | Угол контакта (градусы) | (Ось Y) 1-cos (θSL) |
|---|---|---|---|
| 1 | 27.7 | 10 | 0.0152 |
| 2 | 42.9 | 5 | 0.0038 |
| 3 | 57.2 | 43 | 0.2686 |
| 4 | 64.0 | 50 | 0.3572 |
| 5 | 72.8 | 60 | 0.5000 |
Данные для жидкостей, приведенные в таблице выше, затем отображаются на графике Зисмана (рис.2) с независимой переменной как поверхностное натяжение жидкости в дин / см и зависимой переменной как 1-cos (θSL). Также существуют различные варианты графика Зисмана, поскольку ось Y безразмерна, как показано в Таблице 1 и как указано выше.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Жидкости 1 и 2 полностью смачивают поверхность, о чем свидетельствуют их низкие углы смачивания, поэтому ими следует пренебречь при первом рисовании линии наилучшего соответствия для определения критического поверхностного натяжения жидкости, необходимого для эффективного смачивания поверхности ПК, γC, который является просто пересечением по оси x линии наилучшего соответствия для графика Зисмана. Чтобы найти наиболее подходящую линию, рекомендуется использовать регрессию наименьших квадратов с помощью компьютерной программы, такой как Майкрософт Эксель, Minitab, Matlab, или это также можно сделать с помощью современного графического калькулятора, такого как TI-84. Это было сделано с данными из Таблицы 1, а данные соответствия для жидкостей 3, 4 и 5 показаны на Рисунке 3.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Пересечение x составляет 39,5 дин на сантиметр (это можно вычислить, установив y равным нулю и вычислив x), что меньше, чем у жидкости 2, 42,9 дин на сантиметр; следовательно, более точное измерение критического поверхностного натяжения жидкости, необходимого для эффективного смачивания поверхности ПК, может быть получено путем включения жидкости 2 при создании линии наилучшего соответствия, как показано на Рисунке 4.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Отсечка по оси x здесь составляет 42,1 дин на сантиметр (это можно вычислить, установив y равным нулю и решив x), что указывает на критическое поверхностное натяжение жидкости для ПК.
Резюме
Вклад Уильяма Зисмана в то, что сегодня называют графиком Зисмана, произвел революцию в мире адгезионных соединений и химии поверхностей, предоставив быстрый, эффективный и количественный способ измерения смачиваемости или критического поверхностного натяжения твердого тела. Это породило работу многих других за последние несколько десятилетий. Это простирается от работы Данна в конце 1960-х годов до работы Дэвида и Ноймана в 2014 году. График Зисмана используется и сегодня, и у него много вариаций, поскольку ось Y безразмерна и может быть более легко и точно найдена с помощью современных пакетов программного обеспечения для регрессии. .
Смотрите также
использованная литература
- ^ а б c ЗИСМАН, В.А. (1964-01-01). Контактный угол, смачиваемость и адгезия. Успехи химии. 43. АМЕРИКАНСКОЕ ХИМИЧЕСКОЕ ОБЩЕСТВО. С. 1–51. Дои:10.1021 / ba-1964-0043.ch001. ISBN 0841200440.
- ^ Данн, Дж. Р. (1970). «Силы, участвующие в спаечном процессе». Журнал коллоидной и интерфейсной науки. 32 (2): 302–320. Bibcode:1970JCIS ... 32..302D. Дои:10.1016/0021-9797(70)90054-8.
- ^ Дэвид, Роберт; Нойман, А. Вильгельм (2014). «Картины контактных углов на низкоэнергетических поверхностях». Достижения в области коллоидов и интерфейсной науки. 206: 46–56. Дои:10.1016 / j.cis.2013.03.005.
- Зисман, Связь равновесного краевого угла с жидкостью и твердым телом, 1 января 1964 г., Успехи химии; Американское химическое общество: Вашингтон, округ Колумбия, 1964. doi: 10.1021 / ba-1964-0043.ch001
- Дж. Р. Данн, Критическое поверхностное натяжение твердых полимерных тел, определенное с помощью полярных жидкостей, 16 сентября 1969 г., Journal of Colloid and Interface Science, Volume 32, No. 2, February 1970. doi: 10.1016/0021-9797(70)90054-8
- Дэвид и Нойман, Паттерны контактного угла на поверхности с низкой энергией, 26 марта 2013 г., Достижения в науке о коллоидах и границах раздела, Том 206, апрель 2014 г., страницы 46–56. DOI: 10.1016 / j.cis.2013.03.005

