
Четыре красные точки показывают точки данных, а зеленая точка - точка, в которой мы хотим выполнить интерполяцию.

Пример билинейной интерполяции на единичном квадрате с z значения 0, 1, 1 и 0,5, как указано. Интерполированные значения между ними представлены цветом.
В математика, билинейная интерполяция является продолжением линейная интерполяция для интерполирующий функции двух переменных (например, Икс и y) на прямолинейная 2D сетка.
Билинейная интерполяция выполняется с использованием линейной интерполяции сначала в одном направлении, а затем снова в другом направлении. Хотя каждый шаг линейен по выборочным значениям и позиции, интерполяция в целом не является линейной, а скорее квадратичный в месте пробы.
Билинейная интерполяция - одна из основных повторная выборка методы в компьютерное зрение и обработка изображений, где его еще называют билинейная фильтрация или билинейное наложение текстуры.
Алгоритм
Предположим, что мы хотим найти значение неизвестной функции ж в точке (Икс, y). Предполагается, что мы знаем значение ж в четырех точках Q11 = (Икс1, y1), Q12 = (Икс1, y2), Q21 = (Икс2, y1), и Q22 = (Икс2, y2).
Сначала мы выполняем линейную интерполяцию в Икс-направление. Это дает

Мы продолжаем интерполировать в y-направление для получения желаемой оценки:

Обратите внимание, что мы получим тот же результат, если сначала выполнить интерполяцию по y направлении, а затем по Икс направление.[1]
Альтернативный алгоритм
Альтернативный способ написать решение задачи интерполяции:

где коэффициенты находятся из решения линейной системы

дающий результат

Если решение предпочтительнее с точки зрения ж(Q), то мы можем написать

где коэффициенты находятся путем решения

Площадь единицы
Если мы выберем систему координат, в которой четыре точки, где ж известны (0, 0), (1, 0), (0, 1) и (1, 1), то формула интерполяции упрощается до

или, что эквивалентно, в матричных операциях:


Геометрическая визуализация билинейной интерполяции. Произведение значения в желаемой точке (черный) и всей площади равно сумме произведений значения в каждом углу и частичной площади по диагонали напротив угла (соответствующие цвета).
Нелинейный
Как следует из названия, билинейный интерполянт не линейный; но это продукт двух линейные функции. Например, полученная выше билинейная интерполяция является произведением значений  и
и  .
.
В качестве альтернативы интерполянт на единичном квадрате можно записать как

где

В обоих случаях количество констант (четыре) соответствует количеству точек данных, где ж дано. Интерполянт линейный по линиям параллельно либо к Икс или y направление, эквивалентно, если Икс или y устанавливается постоянной. Вдоль любой другой прямой интерполянт квадратичный. Однако даже если интерполяция не линейный по положению (Икс и y), Это является линейно по амплитуде, как видно из приведенных выше уравнений: все коэффициенты аj, j = 1–4, пропорциональны значению функции ж.
Результат билинейной интерполяции не зависит от того, какая ось интерполируется первой, а какая - второй. Если бы мы сначала выполнили линейную интерполяцию в y направление, а затем в Икс направлении, результирующее приближение будет таким же.
Очевидное расширение билинейной интерполяции до трех измерений называется трилинейная интерполяция.
Применение в обработке изображений

Сравнение Билинейная интерполяция с некоторыми 1- и 2-мерными интерполяциями. Черные и красные / желтые / зеленые / синие точки соответствуют интерполированной точке и соседним отсчетам соответственно. Их высота над землей соответствует их значениям.
В компьютерное зрение и обработка изображений, билинейная интерполяция используется для повторная выборка изображения и текстуры. Алгоритм используется для сопоставления местоположения пикселя экрана с соответствующей точкой на карта текстуры. Средневзвешенное значение атрибутов (цвет, прозрачность и т. Д.) Четырех окружающих тексели вычисляется и применяется к пикселю экрана. Этот процесс повторяется для каждого пикселя, образующего текстурированный объект.[2]
Когда изображение необходимо увеличить, каждый пиксель исходного изображения необходимо переместить в определенном направлении на основе постоянной масштаба. Однако при увеличении изображения с помощью нецелого масштабного коэффициента есть пиксели (т. Е. дыры), которым не присвоены соответствующие значения пикселей. В этом случае те дыры должны быть назначены соответствующие RGB или оттенки серого значения, чтобы в выходном изображении не было пикселей без значений.
Билинейная интерполяция может использоваться там, где невозможно идеальное преобразование изображения с сопоставлением пикселей, чтобы можно было вычислить и присвоить пикселям соответствующие значения интенсивности. В отличие от других методов интерполяции, таких как интерполяция ближайшего соседа и бикубическая интерполяция, билинейная интерполяция использует значения только 4 ближайших пикселей, расположенных по диагонали от данного пикселя, чтобы найти соответствующие значения интенсивности цвета этого пикселя.
Билинейная интерполяция рассматривает ближайшую окрестность 2 × 2 известных значений пикселей, окружающую вычисленное местоположение неизвестного пикселя. Затем требуется средневзвешенное значение этих 4 пикселей для получения окончательного интерполированного значения.[3]
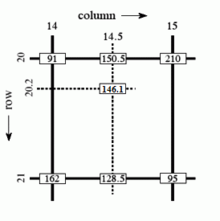
Пример билинейной интерполяции в оттенках серого
Как видно из примера справа, значение интенсивности в пикселе, вычисленное как строка 20.2, столбец 14.5, может быть вычислено путем сначала линейной интерполяции между значениями в столбцах 14 и 15 в каждой строке 20 и 21, давая

а затем линейно интерполируя эти значения, давая

Этот алгоритм уменьшает некоторые визуальные искажения, вызванные изменением размера изображения до нецелого коэффициента масштабирования, в отличие от интерполяции ближайшего соседа, которая заставляет некоторые пиксели казаться больше, чем другие в изображении с измененным размером.
Смотрите также
использованная литература




















