Законы Кассини - Википедия - Cassinis laws

Законы Кассини дать компактное описание движения Луна. Они были основаны в 1693 г. Джованни Доменико Кассини, выдающийся ученый своего времени.[1]

Уточнение этих законов для включения физических либрации были сделаны,[1] и они были обобщены для лечения других спутников и планет.[2][3][4]

Законы Кассини

Наклон орбиты и вращение.
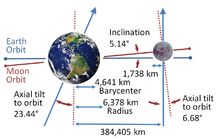
  1. Луна имеет соотношение 1: 1 спин-орбитальный резонанс. Это означает, что вращение –орбита отношение Луны таково, что одна и та же сторона всегда обращена к земной шар.
  2. Ось вращения Луны поддерживает постоянный угол склонность от плоскость эклиптики. Ось вращения Луны прецессирует так, чтобы очертить конус, который пересекает плоскость эклиптики в виде круга.
  3. Самолет, сформированный из нормальный к плоскости эклиптики и нормали к лунной орбитальный самолет будет содержать ось вращения Луны.

В случае Луны ее ось вращения всегда направлена ​​примерно на 1,5 градуса от севера. полюс эклиптики. Нормаль к плоскости орбиты Луны и ее вектор вращения всегда находятся по разные стороны от плоскости эклиптики.

Следовательно, и нормаль к плоскости орбиты, и ось вращения Луны прецессируют вокруг полюса эклиптики с одинаковым периодом. Период составляет около 18,6 лет, а движение ретроградный.

Штат Кассини

Система, подчиняющаяся этим законам, называется Штат Кассини, то есть: развитое вращательное состояние, в котором ось вращения, нормальная орбита и нормальная к Самолет лапласа компланарны, а наклон остается постоянным.[2][3][5] Плоскость Лапласа определяется как плоскость, вокруг которой прецессирует орбита планеты или спутника с постоянным наклоном.[5]

Состояние Кассини 1 определяется как ситуация, в которой как ось вращения, так и нормальная ось орбиты находятся на одной стороне от нормали к плоскости Лапласа. Состояние Кассини 2 определяется как случай, когда ось вращения и нормальная ось орбиты находятся на противоположных сторонах нормали к плоскости Лапласа.[6] Луна Земли находится в состоянии Кассини 2.

Ссылки и примечания

  1. ^ а б Исходное положение законов см. В В Белецкий (2001). Очерки движения небесных тел. Биркхойзер. п. 181. ISBN  3-7643-5866-1.
  2. ^ а б Пил, Стэнтон Дж. (1969). «Обобщенные законы Кассини». Астрономический журнал. 74: 483. Bibcode:1969AJ ..... 74..483P. Дои:10.1086/110825. ISSN  0004-6256.
  3. ^ а б Изебудт, Мари; Марго, Жан-Люк (2006). «Эволюция наклона Меркурия» (PDF). Икар. 181 (2): 327–337. Bibcode:2006Icar..181..327Y. Дои:10.1016 / j.icarus.2005.11.024. ISSN  0019-1035.
  4. ^ В В Белецкий (2001). Очерки движения небесных тел. Birkhäuser. п. 179. ISBN  3-7643-5866-1.
  5. ^ а б Ю. Калисеси (2007). Солнечная изменчивость и планетарный климат. Springer. п. 34. ISBN  0-387-48339-X.
  6. ^ Дж. Н. Винн и М. Дж. Холман (2005), "Наклонные приливы на горячих юпитерах", Астрофизический журнал, Том 628, Выпуск 2, стр. L159-L162.

дальнейшее чтение

Смотрите также