Конвективный планетарный пограничный слой - Convective planetary boundary layer

В конвективный планетарный пограничный слой (CPBL), также известный как дневной планетарный пограничный слой (или просто конвективный пограничный слой, CBL, когда в контексте), является частью нижнего тропосфера наиболее напрямую зависит от солнечного нагрева поверхности земли.^[1]

Этот слой простирается от поверхности земли до насыпи. инверсия который обычно располагается на высоте 1-2 км к полудню над сушей. Ниже инверсии перекрытия (10-60% глубины CBL, также называемой зоной увлечения в дневное время) CBL делится на два подслоя: смешанный слой (35-80% глубины CBL) и поверхностный слой (5-10% глубины CBL). Смешанный слой, основная часть CBL, имеет почти постоянное распределение количеств, таких как потенциальная температура, ветер скорость, влажность и концентрация загрязняющих веществ из-за сильного плавучесть генерируется конвективное турбулентное перемешивание.

Параметризация турбулентного переноса используется для моделирования вертикальных профилей и изменения интересующих величин во времени из-за случайности и неизвестной физики турбулентности. Тем не мение, турбулентность в смешанном слое не является полностью случайным, но часто организован в идентифицируемые структуры, такие как термики и перья в CBL.^[2] Моделирование этих больших водовороты сильно отличается от моделирования небольших вихрей, создаваемых локальными ножницы в поверхностном слое. При параметризации следует учитывать нелокальные свойства больших вихрей.

Средние характеристики

Средние характеристики трех слоев CBL следующие.

Вертикальные профили средних переменных в конвективном пограничном слое. Взято из книги Стулла 1988 г. «Введение в метеорологию пограничного слоя», стр. 13

(1) Поверхностный слой это очень мелководный участок, расположенный близко к земле (нижние 5-10% CBL). Он характеризуется суперадиабатическим скорость отклонения, влажность уменьшается с высотой и сильным сдвиг ветра.^[2] Практически весь сдвиг ветра и весь потенциальный градиент температуры в CBL сосредоточены в приземном слое.

(2) Смешанный слой составляя от 35 до 80% CBL^[2] характеризуется сохраняемыми переменными, такими как потенциальная температура, скорость ветра и влажность.

(3) Зона увлечения (или инверсия кэппинга) может быть довольно толстой, в среднем около 40% глубины CBL. Это область статически стабильного воздуха наверху смешанного слоя, где свободный атмосферный воздух уносится вниз, а термические потоки выходят вверх.^[2] Потенциальная температура и скорость ветра резко возрастает через инверсию покровного слоя, тогда как влажность резко падает.

Эволюция

Глубина CBL имеет сильный суточный цикл с 4-фазным процессом роста.^[3]

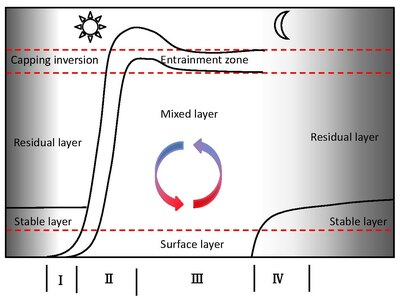
Эволюция конвективного пограничного слоя. Взято из книги Стулла 1988 г. «Введение в метеорологию пограничного слоя», стр. 11

(1) Формирование неглубокого перемешанного слоя: Ранним утром смешанный слой неглубокий, и его глубина медленно увеличивается из-за сильного ночного стабильного инверсионного покрова.^[4]

(2) Стремительный рост : К позднему утру прохладный ночной воздух нагрелся до температуры, близкой к температуре остаточного слоя, поэтому термики быстро проникают вверх во время второй фазы, позволяя верхней части смешанного слоя подниматься со скоростью до 1 км за 15 минут.^[4]

(3) Глубокий смешанный слой почти постоянной толщины: Когда термики достигают инверсии перекрытия в верхней части остаточного слоя, они сталкиваются с сопротивлением вертикальному движению, и скорость роста смешанного слоя быстро уменьшается. Во время этой третьей фазы, которая длится большую часть дня, глубина смешанного слоя относительно постоянна. Перепад температуры в CBL составляет 1 ° / 100 м.^[4]

(4) Разлагаться : Турбулентность создано плавучесть который приводит к затуханию смешения после захода солнца, а также к коллапсу CBL.

Турбулентность в CBL

В пограничном слое атмосферы сдвиг ветра отвечает за горизонтальный перенос тепла, импульс, влажность и загрязняющие вещества, в то время как плавучесть преобладает при вертикальном перемешивании. Турбулентность вызывается плавучесть и сдвиг ветра. Если плавучесть преобладает над созданием сдвига, поток в пограничном слое находится в состоянии свободной конвекции. Когда турбулентность, создаваемая сдвигом, сильнее, чем турбулентность, создаваемая плавучестью, поток находится в состоянии принудительной конвекции.

Нормированная турбулентная кинетическая энергия, генерируемая плавучестью и сдвиг за счет плавучести поверхности. Взято из книги Стулла 1988 г. "Введение в метеорологию пограничного слоя", стр. 155

В поверхностном слое производство сдвига всегда превышает производство плавучести из-за сильного сдвига, создаваемого сопротивлением поверхности. В смешанном слое плавучесть, создаваемая нагревом от поверхности земли, является основным фактором конвективной турбулентности.^[5] Радиационное охлаждение из верхних слоев облаков также является эффективным драйвером конвекции. Пики турбулентности, создаваемой плавучестью, достигаются во второй половине дня, следовательно, поток в пограничном слое находится в состоянии свободной конвекции большую часть дня.

Восходящая и нисходящая конвекция пограничного слоя - это основной способ, которым атмосфера перемещает тепло, импульс, влагу и загрязнители между поверхностью Земли и атмосферой. Таким образом, пограничный слой конвекция играет важную роль в моделировании глобального климата, численном прогнозировании погоды, моделировании качества воздуха и динамике многочисленных мезомасштабных явлений.

Математическое моделирование

Уравнение сохранения

Чтобы количественно описать изменение величин в CBL, нам необходимо решить уравнения сохранения. Упрощенная форма уравнения сохранения для пассивного скаляра в типичном CBL имеет вид

${ displaystyle { frac { partial { bar {c}}} { partial t}} = - { frac { partial { overline {w'c '}}} { partial z}}}$

куда ${ displaystyle { bar {c}}}$ это среднее количество ${ displaystyle c}$ , который может быть соотношением смешивания водяного пара ${ displaystyle q}$ , потенциальная температура ${ displaystyle theta}$ , движущийся на восток ${ displaystyle u}$ и движущихся на север ${ displaystyle v}$ скорость ветра. ${ displaystyle { overline {w'c '}}}$ вертикальный турбулентный поток ${ displaystyle c}$ .

Мы сделали несколько приближений, чтобы получить приведенное выше упрощенное уравнение: игнорировать источник тела, приближение Бусинеска, горизонтальную однородность и отсутствие проседания. Приближение Бусинеска состоит в том, чтобы игнорировать изменение плотности из-за возмущения давления и сохранять изменение плотности из-за изменения температуры. Это довольно хорошее приближение в CBL. Последние два приближения не всегда эффективны в реальном CBL. Но это допустимо в теоретических исследованиях. Наблюдения показывают, что турбулентное перемешивание составляет 50% от общего изменения потенциальной температуры в типичном CBL.

Однако из-за случайности турбулентности и отсутствия у нас знаний о ее точном физическом поведении при моделировании требуется параметризация турбулентного переноса. В отличие от турбулентности с преобладанием сдвига в поверхностном слое, большие водовороты, связанные с подъемом частиц теплого воздуха, переносят тепло от горячего к холодному, независимо от локального градиента фоновой среды, выходящей в смешанный слой. Следовательно, нелокальный противоградиентный перенос должен быть должным образом представлен в моделировании модели.

В численных моделях обычно используются несколько подходов для получения вертикальных профилей и временных изменений величин в CBL. Схема полного смешения для всего CBL, локальная схема для областей с преобладанием сдвига, нелокальная схема и схема диффузии сверху вниз и снизу вверх для смешанного слоя с преобладанием плавучести. В схеме полного перемешивания предполагается, что все величины распределены равномерно, а турбулентные потоки линейно связаны с высотой со скачком вверху. В локальной схеме турбулентный поток масштабируется локальным градиентом величины. В нелокальной схеме потоки турбулентности связаны с известными величинами в любом количестве узлов сетки в другом месте по вертикали.^[6] При нисходящей и восходящей диффузии вертикальный профиль определяется диффузией с двух направлений, а турбулентные потоки в подсеточном масштабе выводятся из известных величин или их вертикальных производных в одной и той же точке сетки.

Полная схема смешивания

Полное смешивание - это простейшее представление CBL в некоторых глобальных моделях. Предполагается, что потоки в этом слое линейно уменьшаются с высотой, а средние переменные сохраняют свой вертикальный профиль на каждом временном шаге моделирования.^[7] Все средние переменные равномерно распределены по всей CBL и имеют скачок в верхней части CBL. Эта простая модель долгое время использовалась в метеорологии и продолжает оставаться популярным подходом в некоторых глобальных моделях разрешения курсов.

Закрытие на месте

Местное закрытие K-теория представляет собой простую и эффективную схему турбулентного переноса с преобладанием сдвига в поверхностном слое. K-теория предполагает, что смешение тепла, водяного пара и концентрации загрязняющих веществ происходит только между соседними слоями CBL, и что величина смешения определяется коэффициентом вихревой диффузии ${ displaystyle K_ {c}}$ и локальные градиенты соответствующих скаляров ${ displaystyle { frac { partial c} { partial z}}}$ .^[8]

${ displaystyle { overline {w'c '}} = - K_ {c} { frac { partial c} { partial z}}}$

Где ${ displaystyle K_ {c}}$ "коэффициент диффузии вихрей" для ${ displaystyle c}$ , которая обычно берется как функция масштаба длины ${ displaystyle l_ {c}}$ и локальные вертикальные градиенты ${ displaystyle c}$ . Для нейтрального состояния ${ displaystyle K_ {c}}$ параметризуется с помощью Теория смешанной длины.

${ displaystyle K_ {c} = l_ {c} ^ {2} left | { frac { partial { bar {u}}} { partial z}} right vert}$

Если турбулентный вихрь перемещает воздушный поток вверх на величину ${ displaystyle z}$ в течение которого не происходит перемешивания или других изменений значения ${ displaystyle c}$ внутри посылки, то мы определяем ${ displaystyle l_ {c}}$ к

${ displaystyle l_ {c} = kappa z}$

куда ${ displaystyle kappa}$ константа Кармана, полученная эмпирическим путем (0,35 или 0,4).

У теории длины смешения есть свои ограничения. Теория применима только к статически нейтральному состоянию.^[9] Он склоняется к статически стабильным и нестабильным условиям.

Теория длины смешения не работает, когда скорость ветра равномерно распределена, люди используют знания о турбулентной кинетической энергии (TKE), чтобы улучшить параметризацию коэффициента диффузии вихрей. ${ displaystyle K_ {c}}$ для учета переноса крупных вихрей в типичном CBL. TKE дает нам меру интенсивности и эффективности турбулентности, и ее можно точно измерить.

${ displaystyle K_ {c} = Sl_ {c} e ^ { text {1/2}}}$

куда ${ displaystyle S}$ - безразмерная функция устойчивости, а ${ displaystyle e}$ это ТКЕ. Диагностические уравнения, используемые для получения параметров ${ displaystyle S}$ и ${ displaystyle l_ {c}}$ отличаются разными затворами ТКЕ.

Нелокальное закрытие

В областях с преобладанием плавучести K-теория не работает, поскольку она всегда дает нереалистичный нулевой поток в однородной среде. Нелокальные характеристики больших вихрей плавучести учитываются путем добавления нелокальной поправки к локальной схеме. Поток любого скаляра ${ displaystyle c}$ можно описать с помощью^[10]

${ displaystyle { overline {w'c '}} = - K_ {c} ({ frac { partial c} { partial z}} - gamma _ {c})}$

куда ${ displaystyle gamma _ {c}}$ является поправкой к локальному градиенту, чтобы представить встречный перенос потока градиента^{[требуется разъяснение ]} крупномасштабные водовороты. В стабильных условиях этот член невелик, и поэтому им пренебрегают. Однако в нестабильных условиях большая часть переноса осуществляется турбулентными вихрями с размерами порядка глубины пограничного слоя.^[10] В таких случаях,

${ displaystyle gamma _ {c} = b { frac { overline {(w'c ') _ {s}}} {w_ {s}}}}$

куда ${ displaystyle { overline {(w'c ') _ {s}}}}$ - соответствующий поверхностный поток для скалярной ${ displaystyle c}$ , и ${ displaystyle b}$ коэффициент пропорциональности. ${ displaystyle w_ {s}}$ - масштаб скорости смешанного слоя, определяемый на основе скорости поверхностного трения и функции профиля ветра в верхней части поверхностного слоя.

Коэффициент диффузии вихрей для импульса определяется как

${ displaystyle K_ {c} = kappa zw_ {s} (1 - { frac {z} {h}}) ^ {2}}$

куда ${ displaystyle kappa}$ - постоянная Кармана, ${ displaystyle z}$ высота над землей, ${ displaystyle h}$ - высота пограничного слоя.

По сравнению со схемой полного смешивания нелокальная схема значительно улучшает моделирование вертикальных распределений NO.₂ и O₃, как было оценено в исследовании, проведенном летом с использованием измерений с самолетов. Это также снижает систематические ошибки модели на поверхности над США на 2-5 частей на миллиард для пика O₃ (O₃ концентрация составляет 40-60ppb) днем, как было оценено с помощью наземных наблюдений.^[7]

Распространение сверху вниз и снизу вверх

В нелокальной схеме потоки увлечения величин не рассматриваются. В схемах сверху вниз и снизу вверх представлены как поверхностные потоки, так и потоки уноса. Средние скалярные потоки - это сумма двух потоков^[11]

${ displaystyle { overline {w'c '}} = { overline {(w'c') _ {s}}} (1-z / h_ {1}) + { overline {(w'c ' ) _ {l}}} (z / h_ {1})}$

Где ${ displaystyle h_ {1}}$ высота смешанного слоя. ${ displaystyle { overline {(w'c ') _ {l}}}}$ и ${ displaystyle { overline {(w'c ') _ {s}}}}$ - скалярный поток вверху и внизу CBL и масштабируется как

Смоделированы вертикальный профиль и турбулентный поток виртуальной потенциальной температуры. По материалам Stull 1988 "Введение в метеорологию пограничного слоя", стр. 457 и Wyngaard and Brost, 1983 г.

${ displaystyle { overline {(w'c ') _ {s}}} = K_ {s} { frac { partial c_ {s}} { partial z}}}$

${ displaystyle { overline {(w'c ') _ {l}}} = K_ {l} { frac { partial c_ {l}} { partial z}}}$

Где ${ displaystyle K_ {s}}$ и ${ displaystyle K_ {l}}$ находятся

${ displaystyle K_ {s} = { frac {w _ {*} h_ {1} (1-z / h_ {1})} {g_ {s}}}}$

${ displaystyle K_ {l} = { frac {w _ {*} z} {g_ {l}}}}$

${ displaystyle w _ {*}}$ - конвективный масштаб скорости ${ displaystyle w _ {*} = (g { overline {w_ {s} theta}} h_ {1} T) ^ { text {1/3}}}$ . ${ displaystyle g_ {b}}$ - безразмерный градиент для направления снизу вверх, функция ${ displaystyle z / h_ {1}}$ . ${ displaystyle g_ {l}}$ - безразмерный градиент сверху вниз. Вертикальный профиль ${ displaystyle g_ {t}}$ и ${ displaystyle g_ {l}}$ представлены в Wyngaard et al., 1983 ^[11]