Метод декомпозиции (удовлетворение ограничений) - Decomposition method (constraint satisfaction)

Эта статья нужны дополнительные цитаты для проверка. Пожалуйста помоги улучшить эту статью к добавление цитат в надежные источники. Материал, не полученный от источника, может быть оспорен и удален. Найдите источники: Выполнение ограничения "метод декомпозиции"  – Новости  · газеты  · книги  · ученый  · JSTOR (Июнь 2019) (Узнайте, как и когда удалить этот шаблон сообщения)

В удовлетворение ограничений, а метод разложения переводит проблема удовлетворения ограничений в другую проблему удовлетворения ограничений, которая является бинарной и ациклический. Методы декомпозиции работают путем группирования переменных в наборы и решения подзадач для каждого набора. Эти переводы сделаны потому, что решение бинарных ациклических задач - это разрешимая проблема.

Каждое структурное ограничение определяло меру сложности решения проблемы после преобразования; эта мера называется ширина. Установка максимально допустимой ширины - это способ определить подкласс проблем удовлетворения ограничений. Решение задач этого класса является полиномиальным для большинства разложений; если это верно для декомпозиции, класс задач фиксированной ширины образует управляемый подкласс задач удовлетворения ограничений.

Обзор

Методы декомпозиции переводят проблему в новую, которую легче решить. Новая задача содержит только бинарные ограничения; их масштабы образуют ориентированный ациклический граф. Каждая переменная новой задачи представляет собой набор переменных исходной. Эти наборы не обязательно не пересекаются, но они покрывают набор исходных переменных. Перевод находит все частные решения относительно каждого набора переменных. Проблема, возникающая в результате перевода, представляет собой взаимодействие между этими локальными решениями.

По определению, метод декомпозиции создает двоичную ациклическую проблему; такие задачи могут быть решены за полиномиальное по своим размерам время. В результате исходную проблему можно решить, сначала переведя ее, а затем решив полученную проблему; однако этот алгоритм является полиномиальным только в том случае, если разложение не увеличивает размер суперполиномиально. В ширина метода декомпозиции - это мера размера возникшей проблемы. Первоначально ширина определялась как максимальная мощность множества исходных переменных; один метод, разложение гипердерева, использует другую меру. В любом случае ширина декомпозиции определяется таким образом, чтобы декомпозиции размера, ограниченного константой, не создавали слишком больших проблем. Экземпляры, имеющие разложение фиксированной ширины, могут быть переведены путем разложения в экземпляры размера, ограниченного полиномом от размера исходного экземпляра.

Ширина проблемы - это ширина ее разложения минимальной ширины. Хотя разложения фиксированной ширины могут использоваться для эффективного решения проблемы, ограничение ширины экземпляров обязательно дает послушный структурное ограничение. Действительно, задача фиксированной ширины имеет декомпозицию фиксированной ширины, но ее нахождение не может быть полиномиальным. Для того чтобы проблема фиксированной ширины была эффективно решена посредством разложения, необходимо эффективно найти одно из ее разложений с малой шириной. По этой причине методы декомпозиции и связанная с ними ширина определены таким образом, что не только решение задачи с учетом ее разложения фиксированной ширины является полиномиальным временем, но также обнаружение разложения фиксированной ширины задачи фиксированной ширины является полиномиальным - время.

Методы разложения

Методы декомпозиции создают задачу, которую легко решить из произвольной. Каждая переменная этой новой проблемы связана с набором исходных переменных; его домен содержит кортежи значений переменных в соответствующем наборе; в частности, это кортежи, которые удовлетворяют набору ограничений на эти переменные. Ограничения новой задачи ограничивают значения двух новых переменных, чтобы иметь в качестве значений два кортежа, которые согласуются с общими исходными переменными. Три дополнительных условия гарантируют, что новая проблема эквивалентна старой и может быть эффективно решена.

Для эффективного решения новой проблемы необходимо прямой граф новой задачи требуется, чтобы она была ацикличной. Другими словами, если рассматривать переменные как вершины, а (бинарные) ограничения как ребра, результирующий граф должен быть дерево или лес.

Чтобы новая проблема была эквивалентна старой, каждое исходное ограничение применяется как часть определения области по крайней мере одной новой переменной. Это требует, чтобы для каждого ограничения старой проблемы существовала такая переменная новой проблемы, чтобы связанный с ней набор исходных переменных включал область действия ограничения, а все кортежи в ее области удовлетворяли этому ограничению.

Еще одно условие, необходимое для обеспечения эквивалентности, заключается в том, что двоичных ограничений достаточно, чтобы заставить все «копии» каждой исходной переменной принимать одно и то же значение. Поскольку одна и та же исходная переменная может быть связана с несколькими новыми переменными, все значения этой новой переменной должны соответствовать значению старой переменной. Бинарные ограничения используются для обеспечения равенства старых переменных, совместно используемых двумя новыми переменными. Две копии новой переменной принудительно равны, если существует путь двоичных ограничений между их новыми переменными и все новые переменные в этом пути содержат старую переменную.

	Пример проблемы удовлетворения ограничений; эта задача бинарная, и ограничения представлены ребрами этого графа.
	Дерево разложения; для каждого ребра исходного графа есть узел, содержащий обе его конечные точки; все узлы, содержащие переменную, связаны
	Решение подзадачи. В этом примере показано решение подзадачи, состоящей из всех ограничений на переменные первого набора. ${displaystyle {x, y, z}}$. Аналогичная процедура проделывается и для других наборов. ${displaystyle {u, x, z}}$ и ${displaystyle {y, w}}$
	Каждый узел дерева делается переменной. Его предметной областью является множество решений частичной задачи, которая представляет собой набор кортежей. Ограничения новой задачи допускают только кортежи, содержащие равные значения исходных переменных. На рисунке равенство ${displaystyle y}$ отображается: соответствующее ограничение выполняется только первым кортежем ${displaystyle (x, y, z)}$ и первый кортеж ${displaystyle (y, w)}$, а по второму набору ${displaystyle (x, y, z)}$ и второй кортеж ${displaystyle (y, w)}$. Более того, второй набор${displaystyle (x, y, z)}$ не может найти удовлетворяющий кортеж в своем левом дочернем элементе (${displaystyle (u, x, z)}$). Таким образом, второй набор ${displaystyle (u, x, z)}$ следует удалить.

Метод декомпозиции обычно определяется путем предоставления дерева, узлы которого являются переменными новой проблемы; для каждого узла также предоставляется связанный набор исходных переменных и, возможно, набор исходных ограничений, используемых для построения области определения переменной в новой задаче. Из трех вышеуказанных условий (древовидная структура, соблюдение ограничений и эквивалентность копий исходных переменных) первое автоматически обеспечивается этим определением. Условие принуждения ограничений в основном формулируется следующим образом: объем каждого ограничения - это подмножество переменных некоторого узла; однако может использоваться другое условие, когда узлы также связаны с наборами ограничений. Эквивалентность всех копий исходных переменных обычно формулируется так: подграф, индуцированный узлами, связанными с исходной переменной, связан.

Методы декомпозиции бинарных задач

Существует ряд методов декомпозиции. Большинство из них создают управляемый класс, ограничивая ширину экземпляров. Ниже приведены методы декомпозиции, определенные для задач удовлетворения двоичных ограничений. Поскольку проблему можно сделать двоичной, переведя ее в двойная проблема или используя скрытые переменные, эти методы могут косвенно использоваться для предоставления дерева декомпозиции для произвольных задач удовлетворения ограничений.

Двухсвязные компоненты

В теории графов разделяющая вершина это узел графа, который "ломает" граф при удалении из него. Формально это узел, удаление которого из графа увеличивает количество его компонент связности. А двусвязный компонент графа - это максимальное множество его узлов, индуцированный подграф которого связен и не имеет разделяющей вершины. Из теории графов известно, что двусвязные компоненты и разделяющие вершины графа образуют дерево. Это дерево можно построить следующим образом: его узлами являются двусвязные компоненты и разделяющие вершины графа; ребра только соединяют двусвязный компонент с разделяющей вершиной, и, в частности, это происходит, если вершина содержится в компоненте. Можно доказать, что этот граф на самом деле является деревом.

Если ограничения задачи удовлетворения двоичных ограничений рассматриваются как ребра графа, узлы которого являются переменными, это дерево представляет собой декомпозицию проблемы. Ширина разбиения - это максимальное количество вершин в двусвязном компоненте.

Простой граф задачи удовлетворения ограничений (каждый узел представляет переменную, а каждое ребро - ограничение между двумя переменными)	Его двусвязные компоненты (цветные) и его разделяющие вершины (черные, в данном случае только одна)	Двусвязная декомпозиция: узлы дерева разделяют вершины и двусвязные компоненты

Цикл Cutset

Метод декомпозиции цикла разбивает задачу на циклическую и ациклическую части. Хотя это не соответствует определению других методов декомпозиции, которые создают дерево, узлы которого помечены наборами узлов, его можно легко переформулировать в таких терминах.

Этот метод декомпозиции основан на идее, что после того, как некоторым переменным присвоено значение, то, что остается от проблемы после того, как эти переменные были исключены, может быть ациклическим. Формально набор циклов графа - это набор узлов, которые делают граф ацикличным, когда они удаляются из него. Аналогичное определение может быть дано для задачи удовлетворения ограничений с использованием ее прямого графа. Ширина разложения цикла - это количество переменных в разрезе. Ширина задачи - это минимальная ширина ее циклических декомпозиций.

Графическое представление проблемы удовлетворения ограничений	Циклическое сечение графа (существуют и другие)	После удаления сечения циклов остается ациклический граф (в данном случае дерево, но в целом лес).

Выбрав узел b в качестве корня, это дерево, аналогичное тем, которые созданы другими методами декомпозиции.

Такое разложение не вписывается в схему других разложений, потому что результатом разложения является не дерево, а скорее набор переменных (те, что входят в набор сечений) и дерево (образованное переменными, не входящими в набор сечения). Однако дерево, подобное тем, которые сгенерированы другими методами декомпозиции, можно получить из дерева, полученного в результате удаления набора сечений; это делается путем выбора корня, добавления всех переменных сечения ко всем его узлам и переменных каждого узла ко всем его дочерним элементам. В результате получается дерево, максимальное количество переменных, связанных с узлом, равно размеру сечения плюс два. Помимо добавления двух, это ширина разложения, которая определяется как количество переменных в рассматриваемом сечении.

К сожалению, определение минимального набора для удаления NP-сложная проблема.

Разложение дерева

Разложение дерева это хорошо известная концепция из теории графов. Переформулированная в терминах двоичных ограничений, разложение дерева - это дерево, узлы которого связаны с наборами переменных; объем каждого ограничения содержится в наборе переменных некоторого узла, и поддерево узлов, связанных с каждой переменной, связано. Это наиболее общая форма декомпозиции бинарных ограничений, которая следует схеме, описанной выше, поскольку на дерево накладываются только те условия, которые необходимы для гарантии эквивалентности исходной и новой задачи.

Ширина такого разложения равна максимальному количеству переменных, связанных с одним и тем же узлом, минус один. В ширина дерева задачи - это минимальная ширина ее древовидных разложений.

Устранение ведра может быть переформулирован как алгоритм, работающий на декомпозиции определенного дерева. В частности, при заданном порядке переменных каждая переменная связана с корзиной, содержащей все ограничения, так что переменная является наибольшей в их области действия. Исключение сегмента соответствует разложению дерева, которое имеет узел для каждого сегмента. Этот узел связан со всеми своими ограничениями и соответствует набору всех переменных этих ограничений. Родитель узла, связанный с корзиной ${displaystyle x_ {i}}$ узел, связанный с ведром ${displaystyle x_ {j}}$, куда ${displaystyle x_ {j}}$ наибольший узел, который находится в ограничении с ${displaystyle x_ {i}}$ и предшествует ${displaystyle x_ {i}}$ в заказе.

Методы декомпозиции для произвольных задач

Следующие методы могут использоваться для преобразования произвольной задачи удовлетворения ограничений, как двоичной, так и другой. Поскольку они также могут использоваться для двоичных задач, их также можно использовать в результате создания двоичных ограничений, либо путем преобразования в двойная проблема или используя скрытые переменные.

Некоторые из этих методов связывают ограничения с узлами дерева и определяют ширину с учетом количества ограничений, связанных с узлами. Это может уменьшить ширину некоторых проблем. Например, разложение, в котором десять переменных связаны с каждым узлом, имеет ширину десять; однако, если каждый из этих наборов из десяти переменных является областью ограничения, вместо этого с каждым узлом может быть связано это ограничение, в результате чего ширина будет равна единице.

Двухсвязные компоненты

Двусвязная декомпозиция произвольной задачи удовлетворения ограничений - это двусвязная декомпозиция ее прямого графа. Каждое ограничение может быть применено к узлу дерева, потому что каждое ограничение создает клику для своих переменных на прямом графе, а клика является либо двусвязным компонентом, либо подмножеством двусвязного компонента.

Разложение дерева

Древовидная декомпозиция произвольной задачи удовлетворения ограничений - это древовидная декомпозиция ее прямого графа. Каждое ограничение может быть применено к узлу дерева, потому что каждое ограничение создает клику для своих переменных на прямом графе, и для каждой декомпозиции дерева переменные клики полностью содержатся в переменных некоторого узла.

Cycle hypercutset

Это тот же метод циклического сечения, использующий определение сечения для гиперграфов: циклическое гипер-сечение гиперграфа - это набор ребер (а не вершин), который делает гиперграф ацикличным, когда все их вершины удалены. Декомпозицию можно получить, сгруппировав все переменные гиперпреобразователя в одну. Это приводит к дереву, узлы которого являются наборами гиперребер. Ширина такой декомпозиции - это максимальный размер наборов, связанных с узлами, который равен единице, если исходная задача является ациклической, и размером ее минимального гиперсечения в противном случае. Ширина задачи - это минимальная ширина ее разложений.

Разложение петли

Шарнир - это подмножество узлов гиперграфа, обладающее некоторыми свойствами, определенными ниже. Разложение по шарниру основано на наборах переменных, которые являются минимальными шарнирами гиперграфа, узлы которого являются переменными задачи удовлетворения ограничений, а гиперребра являются областями его ограничений.

Определение петли следующее. Позволять ${displaystyle H}$ быть набором гиперребер. Путь к. ${displaystyle H}$ - последовательность ребер такая, что пересечение каждого из них со следующим непусто и не содержится в узлах ${displaystyle H}$. Набор ребер связан с. ${displaystyle H}$ если для каждой пары его ребер существует путь относительно ${displaystyle H}$ из которых два узла являются первым и последним ребром. Связный компонент w.r.t. ${displaystyle H}$ - максимальное множество связных ребер относительно ${displaystyle H}$.

Шарниры определены для редуцированных гиперграфов, которые представляют собой гиперграфы, в которых ни одно гиперребро не содержится в другом. Набор минимум из двух ребер ${displaystyle H}$ является шарниром, если для каждого связного компонента ${displaystyle F}$ w.r.t. ${displaystyle H}$, все узлы в ${displaystyle F}$ которые также находятся в ${displaystyle H}$ все содержатся в одном ребре ${displaystyle H}$.

Разложение на шарниры основано на соответствии между задачами удовлетворения ограничений и гиперграфами. Гиперграф, связанный с проблемой, имеет переменные проблемы, поскольку узлы являются областями ограничений в виде гиперребер. Разбиение на шарниры проблемы удовлетворения ограничений - это дерево, узлы которого являются некоторыми минимальными шарнирами гиперграфа, ассоциированного с проблемой, и такое, что выполняются некоторые другие условия. Согласно соответствию задач гиперграфам, шарнир - это набор областей ограничений, и поэтому его можно рассматривать как набор ограничений. Дополнительные условия определения шарнирной декомпозиции - три, из которых первые два обеспечивают эквивалентность исходной задачи новой. Двумя условиями эквивалентности являются: область действия каждого ограничения содержится по крайней мере в одном узле дерева, и поддерево, индуцированное переменной исходной задачи, связано. Дополнительным условием является то, что если два узла соединены, то они разделяют ровно одно ограничение, а область действия этого ограничения содержит все переменные, общие для двух узлов.

Максимальное количество ограничений узла одинаково для всех петлевых декомпозиций одной и той же задачи. Этот номер называется степень цикличности проблемы или ее ширины петли.

Кластеризация деревьев

Кластеризация дерева или кластеризация дерева соединений основана на ограничениях слияния, поэтому в результате возникает проблема присоединиться к дереву, это дерево соединения является результатом декомпозиции.

Дерево соединения проблемы удовлетворения ограничений - это дерево, в котором каждый узел связан с ограничениями (и наоборот), и такое дерево, что подключается поддерево узлов, ограничение которых содержит переменную. В результате создание дерева соединений можно рассматривать как особую форму декомпозиции, где каждый узел дерева связан с областью ограничения.

Не все проблемы удовлетворения ограничений имеют дерево соединений. Однако проблемы можно изменить, чтобы получить дерево соединений, объединив ограничения. Кластеризация дерева основана на том факте, что проблема имеет дерево соединений тогда и только тогда, когда ее первичный граф хордовый и соответствующий с проблемой, последнее означает, что переменные каждого максимальная клика первичного графа являются областью ограничения и наоборот. Кластеризация дерева модифицирует произвольную задачу таким образом, чтобы выполнялись эти два условия. Хордальность обеспечивается путем добавления новых двоичных ограничений. Соответствие достигается путем объединения ограничений.

В частности, хордальность обеспечивается путем добавления к проблеме некоторых «поддельных» двоичных ограничений. Это бинарные ограничения, которым удовлетворяет любая пара значений, и используются только для добавления ребер к прямому графу задачи. В частности, хордальность получается путем добавления ребер, образующих индуцированный граф прямого графа в произвольном порядке. Эта процедура верна, потому что индуцированный граф всегда хордовый и получается добавлением ребер к исходному графу.

Конформность требует, чтобы максимальные клики прямого графа точно соответствовали области ограничений. Хотя область действия каждого исходного ограничения - клика на прямом графе, эта клика не обязательно является максимальной. Более того, даже если изначально он был максимальным, усиление хордальности может создать большую клику. Соответствие обеспечивается объединением ограничений. В частности, для каждой максимальной клики графа, возникающей в результате принудительной хордальности, создается новое ограничение с кликой в ​​качестве области видимости. Удовлетворяющие значения этого нового ограничения - это те, которые удовлетворяют всем исходным ограничениям, область действия которых содержится в клике. Благодаря этому преобразованию каждое исходное ограничение «включается» по крайней мере в одно новое ограничение. В самом деле, область видимости каждого исходного ограничения - это клика прямого графа. Эта клика остается кликой даже после применения хордальности, так как этот процесс только вводит новые ребра. В результате эта клика либо максимальная, либо содержится в максимальной клике.

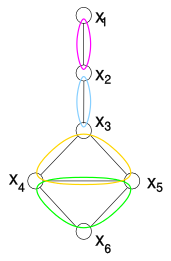Пример: проблема удовлетворения двоичного ограничения (кластеризация дерева соединений также может применяться к небинарным ограничениям). Этот граф не хордовый (x3x4x5x6 образуют цикл из четырех узлов, не имеющих хорды).	График сделан хордовым. Алгоритм анализирует узлы от x6 до x1. Красное ребро - единственное добавленное ребро, потому что x6 - единственный узел, имеющий два несвязанных родителя. Он представляет собой ограничение между x4 и x5, которому удовлетворяет каждая пара значений.	Выявляются максимальные клики полученного графа. Кластеризация дерева соединения заменяет ограничения на {x3, x4, x5, x6} двумя эквивалентными ограничениями, одно на {x3, x4, x5} и одно на {x4, x5, x6}.

Этот перевод требует определения максимальных клик хордального графа. Однако это можно легко сделать, используя тот же порядок, который используется для обеспечения хордальности. Поскольку все родители каждого узла связаны друг с другом, максимальные клики состоят из узла (максимального узла клики в порядке максимальной мощности) и всех его родителей. В результате эти максимальные клики можно обнаружить, рассматривая каждый узел с его родителями.

Проблема, возникающая в результате этого процесса, связана с деревом соединений, и такое дерево соединений можно получить, снова используя тот же порядок переменных. Начиная с последнего узла к первому, каждое ограничение связано с предыдущим ограничением, которое разделяет с ним больше переменных. Кластеризацию дерева соединений можно рассматривать как метод декомпозиции, в котором:

• элементы покрытия - это клики графа, полученные в результате принудительной хордальности;
• дерево - это дерево соединений;
• каждое ограничение назначается всем узлам дерева, наборы переменных которых содержат область действия ограничения.

Ширина разложения на кластеры дерева - это максимальное количество переменных, связанных с каждым узлом дерева. Ширина проблемы - это минимальная ширина ее разложений по дереву.

Разложение на шарниры / кластеры

Результат декомпозиции шарнира можно дополнительно упростить, разложив каждый шарнир с помощью кластеризации дерева. Другими словами, как только петли идентифицированы, создается дерево кластеров каждой из них. Таким образом, с точки зрения результирующего дерева каждый узел заменяется деревом.

Декомпозиция запроса

Декомпозиция запроса связывает набор переменных и набор ограничений с каждым узлом дерева; каждое ограничение связано с некоторым узлом, а поддерево, индуцированное узлами, связанными с данной переменной или ограничением, связано. Точнее, для каждой переменной связано поддерево узлов, связанных с этой переменной или с ограничением, имеющим эту переменную в своей области действия. Ширина декомпозиции - это максимальное объединенное количество переменных и ограничений, связанных с узлом.

Связывание ограничений с узлами может уменьшить ширину декомпозиций и экземпляров. С другой стороны, это определение ширины по-прежнему позволяет решать задачи фиксированной ширины за полиномиальное время, если дано разложение. В этом случае область определения новой переменной получается путем решения подзадачи, которая может быть полиномиально большой, но имеет фиксированное количество ограничений. В результате эта область гарантированно будет иметь полиномиальный размер; ограничения новой задачи, являющиеся равенствами двух областей, также полиномиальны по размеру.

Гиперграфическое представление проблемы удовлетворения ограничений: ограничениям даны имена (P, Q, R, S, T) и показаны их области действия (P (a, b, c) означает, что ограничение P относится к переменным {a , до н.э}

Разложение проблемы на запрос. Узлы могут содержать переменные, ограничения или и то, и другое. Хотя с крайним правым узлом связаны всего пять переменных (то есть a, b, c, d, e среди двух ограничений), это разложение ширины 3, потому что ни один узел не содержит более трех ограничений и изолированных переменных (существует другое разложение ширины 2, и можно показать, что это разложение ширины 2 является минимальной шириной этого гиперграфа).

А чистая декомпозиция запроса представляет собой разложение запроса, в котором узлы связаны только с ограничениями. Из разложения запроса заданной ширины можно построить в логарифмическом пространстве чистую декомпозицию запроса той же ширины. Это достигается заменой переменных узла, которые не входят в ограничения узла, некоторыми ограничениями, которые содержат эти переменные.

Недостатком этого метода декомпозиции является то, что проверка того, имеет ли экземпляр фиксированную ширину, обычно НП-полный; это было доказано для ширины 4

Разложение гипердерева

Декомпозиция гипердерева связывает набор переменных и набор ограничений с каждым узлом дерева. Он расширяет декомпозицию запроса, позволяя ограничениям узла содержать переменные, которые не используются при создании домена новой переменной, связанной с узлом. Помимо общих условий для метода декомпозиции (область действия каждого ограничения находится, по крайней мере, в наборе переменных, связанных с узлом, и поддерево, индуцированное исходной переменной, связано), должны выполняться следующие два условия:

1. каждая исходная переменная в узле находится в области действия по крайней мере одного ограничения, связанного с узлом;
2. переменные ограничений узла, которые не являются переменными узла, не встречаются в поддереве с корнем в узле.

Ширина разложения дерева - это максимальное количество ограничений, связанных с каждым узлом. Если эта ширина ограничена константой, задача, эквивалентная исходной, может быть построена за полиномиальное время. Переменные, которые не связаны с узлом, но находятся в области ограничений узла, «проецируются» при построении этого экземпляра. Это можно сделать, сначала спроецировав ограничения на переменные узла и затем найдя все решения этой подзадачи, или сначала решив подзадачу со всеми ограничениями, а затем удалив лишние переменные.

Декомпозиция гипердерева той же проблемы декомпозиции запроса выше. R (b, d, e, -) означает, что последняя переменная R не является переменной, связанной с корнем. Группируя две переменные в одно ограничение в корне, ширина уменьшается с трех до двух.

Два вышеуказанных требования не являются необходимыми для гарантии эквивалентности исходной и новой задачи. Они необходимы, чтобы гарантировать, что задачи ограниченной ширины могут быть решены за полиномиальное время.

Возможность связать ограничение с узлом, в то время как некоторые из его переменных не связаны эффективно с узлом, может привести к ширине, меньшей, чем ширина запроса. Например, если узел связан с ${displaystyle {C (a, b), c, d, e}}$ в декомпозиции запроса и ограничение ${displaystyle D (c, d, e, f)}$ существует, разложение гипердерева может связать тот же узел с ограничениями ${displaystyle {C, D}}$ и переменные ${displaystyle {a, b, c, d, e}}$. Поскольку при проверке ширины вычисляются только ограничения, этот узел имеет ширину два. Тот же узел имеет ширину четыре при использовании декомпозиции запроса (одно ограничение и три переменные). Это уменьшение ширины возможно, если две или более переменных могут быть заменены одним ограничением, даже если это ограничение содержит переменную, не связанную с узлом.

Обобщенная декомпозиция гипердерева

Обобщенные декомпозиции гипердерева определяются как декомпозиции гипердерева, но последнее требование опускается; это условие «переменные ограничений узла, которые не являются переменными узла, не встречаются в поддереве с корнем в узле». Проблема может быть решена за полиномиальное время, если дано ее разложение фиксированной ширины. Тем не менее, ограничение фиксированной ширины, как известно, не поддается выполнению, поскольку сложность нахождения разложения фиксированной ширины, даже если известно, что оно существует, не известна, по состоянию на 2001 год.^{[Обновить]}.

Сравнение

Ширина экземпляров - это форма эффективности методов декомпозиции. Действительно, учитывая, что проблемы могут быть решены с помощью декомпозиции фиксированной ширины, чем меньше ширина согласно декомпозиции, тем больше примеров можно эффективно решить с помощью этой декомпозиции.

В некоторых декомпозициях в качестве ширины используется количество переменных узла (или аналогичное количество). Другие не связывают ограничения (или их области в форме гиперребер) с узлами и включают в себя количество ограничений, связанных с узлом по ширине, не связывают: гипервизор цикла, декомпозиция петель, декомпозиция запросов, декомпозиция гипердерева и обобщенная декомпозиция гипердерева. Это может дать значительную экономию по ширине. Действительно, проблемы с одним ограничением на ${displaystyle n}$ переменные можно разложить только на дерево с одним узлом. Этот узел может быть связан с ${displaystyle n}$ переменные или с одним ограничением. Подсчет количества переменных приводит к ширине ${displaystyle n}$, а подсчет количества ограничений приводит к ширине ${displaystyle 1}$.

Сравнение всех других методов разложения основано на обобщении и биении. Обобщение означает, что каждая проблема, имеющая ширину ${displaystyle n}$ по способу имеет ширину, ограниченную ${displaystyle n + k}$ для фиксированного ${displaystyle k}$. Превышение означает, что существуют классы задач, которые имеют фиксированную ширину в соответствии с методом декомпозиции, но не в соответствии с другим. Ниже приведены результаты для произвольных задач, в которых не рассматривается декомпозиция запроса:

• декомпозиция гипердерева обобщает и превосходит все другие методы
• разложение по петлям, усиленное кластеризацией деревьев, обобщает и опережает как разложение по петлям, так и кластеризацию деревьев
• кластеризация деревьев эквивалентна декомпозиции дерева (на прямом графе)
• как разложение по петлям, так и кластеризация деревьев обобщают и побеждают двусвязные компоненты
• набор циклов (на простом графе) обобщен и побежден как гиперсечением цикла, так и кластеризацией дерева

Также можно показать, что ширина кластеризации дерева равна наведенная ширина проблемы плюс один. Алгоритм адаптивная согласованность, который является полиномом для задачи фиксированной индуцированной ширины, превращает задачи в эквивалентные так же, как первый шаг кластеризации дерева.

Решение из разложения

Учитывая дерево декомпозиции, решение может быть выполнено путем построения бинарной древовидной проблемы, как описано выше, и ее решения. Это задача с полиномиальным временем, поскольку ее можно решить за полиномиальное время, используя, например, алгоритм для обеспечения согласованность направленной дуги.

Специализированный алгоритм для случая бинарных ациклических задач, возникающих в результате декомпозиции, описывается следующим образом. Он работает путем создания ограничений, которые передаются по краям дерева от листьев к корню и обратно. Ограничение, переданное по ребру, «суммирует» эффекты всех ограничений части графа с одной стороны ребра на другую.

Ограничение, передаваемое от узла i к узлу j, суммирует влияние узлов на «стороне» i на переменные j.

В дереве каждое ребро разбивает граф на две части. Ограничение, передаваемое вдоль ребра, сообщает, как часть исходного конца ребра влияет на переменные целевого узла. Другими словами, ограничение, переданное от узла ${displaystyle i}$ узел ${displaystyle j}$ рассказывает, как узлы "на стороне ${displaystyle i}$"ограничить переменные узла ${displaystyle j}$.

Если переменные этих двух узлов равны ${displaystyle X_ {i}}$ и ${displaystyle X_ {j}}$, узлы размером ${displaystyle i}$ не влияют на все переменные ${displaystyle X_ {j}}$ но только общие переменные ${displaystyle X_ {i} cap X_ {j}}$. В результате влияние на ${displaystyle X_ {j}}$ узлов на стороне ${displaystyle i}$ можно представить как ограничение на переменные ${displaystyle X_ {i} cap X_ {j}}$. Такое ограничение можно рассматривать как «сводку» того, как набор узлов влияет на другой узел.

Алгоритм исходит из листьев дерева. В каждом узле собираются сводки его дочерних узлов (если есть). Эта сводка и ограничение узла используются для создания сводки узла для его родителя. Когда корень достигнут, процесс инвертируется: создается сводка каждого узла для каждого дочернего элемента и отправляется. Когда все листья достигнуты, алгоритм останавливается.

Дерево декомпозиции со связанными ограничениями. В этом примере все переменные имеют домен {0, .., 10}.	Самый левый узел содержит ограничение a 0 отправляется своему родительскому элементу.	Левый дочерний элемент корня получает ограничение b> 0 и объединяет его со своим ограничением b 1. Это ограничение отправляется своему родителю.	Когда корень получил ограничения для всех своих потомков, он объединяет их и отправляет им обратно. Процесс заканчивается, когда будут достигнуты все листья. На этом этапе допустимые значения переменных указаны явно.

Набор переменных, совместно используемых двумя узлами, называется их разделитель. Поскольку разделитель является пересечением двух наборов, связанных с узлами, его размер не может быть больше, чем индуцированная ширина графа.

В то время как ширина графа влияет на время, необходимое для решения подзадач в каждом узле, размер разделителя влияет на размер ограничений, которые передаются между узлами. Действительно, у этих ограничений есть разделители в качестве области видимости. В результате ограничение на разделитель размера ${displaystyle n}$ может потребоваться размер ${displaystyle d ^ {n}}$ для сохранения, если все переменные имеют домен размера ${displaystyle d}$.

Компромисс между памятью и временем

Алгоритм решения проблемы из дерева декомпозиции включает две операции: решение подзадачи относительно узла и создание ограничения относительно общих переменных (разделителя) между двумя узлами. Для этих двух операций можно использовать разные стратегии. В частности, создание ограничений для разделителей может быть выполнено с использованием исключения переменных, что является формой вывода, в то время как подзадачи могут быть решены с помощью поиска (обратное отслеживание и т. Д.)

Проблема с этим алгоритмом заключается в том, что ограничения, передаваемые между узлами, могут иметь экспоненциальный размер по размеру разделителя. Объем памяти, необходимой для хранения этих ограничений, можно уменьшить, используя разложение по дереву с небольшими разделителями. Однако такие деревья декомпозиции могут иметь ширину (количество узлов в каждом узле) больше оптимальной.

Для данного дерева декомпозиции фиксированный максимально допустимый размер разделителя может быть обеспечен путем объединения всех пар узлов, разделитель которых больше этого размера. Слияние двух узлов обычно создает узел со связанным набором переменных, больший, чем у этих двух узлов. Это может увеличить ширину дерева. Однако это слияние не меняет разделителей дерева, кроме удаления разделителя между двумя объединенными узлами.

Последнее является следствием ацикличности: два соединенных узла не могут быть соединены с одним и тем же другим узлом. Если ${displaystyle n_ {1}}$ и ${displaystyle n_ {2}}$ два узла, которые нужно объединить и ${displaystyle N_ {1}}$ и ${displaystyle N_ {2}}$ - присоединенные к ним наборы узлов, то ${displaystyle N_ {1} cap N_ {2} = emptyset}$, иначе в дереве был бы цикл. В результате узел, полученный объединением ${displaystyle n_ {1}}$ и ${displaystyle n_ {2}}$ будет присоединен к каждому из узлов ${displaystyle N_ {1} чашка N_ {2}}$. В результате разделители этого объединенного узла являются в точности разделителями двух исходных узлов.

В результате слияние пары узлов, соединенных разделителем, не изменяет другие разделители. В результате можно обеспечить фиксированный максимальный размер разделителя, сначала вычислив все размеры разделителей, а затем итеративно объединяя любую пару узлов, имеющих разделитель, превышающий заданное количество, и при этом размер разделителей не нужно пересчитывать во время выполнения.

Структурные ограничения

Ограничение ширины метода декомпозиции константой создает структурное ограничение, то есть ограничивает возможные области ограничений, но не их отношения. Дополнительным способом получения поддающихся обработке подклассов удовлетворения ограничений является наложение ограничений на отношения ограничений; они называются реляционное ограничение, а набор разрешенных отношений называется язык ограничений.

Если решение задач, имеющих ширину декомпозиции, ограниченную константой, находится в п, разложение приводит к послушному структурному ограничению. Как объяснялось выше, послушность требует соблюдения двух условий. Во-первых, если ширина задачи ограничена константой, то разложение ограниченной ширины может быть найдено за полиномиальное время. Во-вторых, задача, полученная преобразованием исходной задачи согласно декомпозиции, не будет суперполиномиально больше, чем исходная задача, если декомпозиция имеет фиксированную ширину.

В то время как наиболее приемлемые структурные ограничения связаны с фиксированием ширины метода декомпозиции, были разработаны другие. Некоторые из них могут быть переформулированы в терминах методов декомпозиции: например, ограничение двоичной ациклической проблемы может быть переформулировано как проблема ширины дерева 1; ограничение на индуцированную ширину (которое не определяется в терминах разложения) можно переформулировать как кластеризацию дерева.

Раннее структурное ограничение (которое позже превратилось в ограничение, основанное на индуцированной ширине) основано на ширине первичного графа задачи. Учитывая порядок узлов графа, ширина узла - это количество узлов, которые присоединяются к нему и предшествуют ему в порядке. Однако ограничение только ширины не ведет к сговорчивому ограничению: даже при ограничении этой ширины до 4 установление выполнимости остается. НП-полный. Сговорчивость достигается ограничением отношений; в частности, если проблема имеет ширину ${displaystyle k}$ и сильно ${displaystyle k}$-согласованны, эффективно решаемы. Это ограничение не является ни структурным, ни реляционным, так как оно зависит как от масштабов, так и от отношений ограничений.

Смотрите также

• Разложение дерева в теории графов
• Алгоритм Junction Tree используется в машинном обучении для извлечения маргинализации в общих графах.

Интернет-ресурсы

Вот несколько ссылок на онлайн-ресурсы по декомпозиции дерева / гипердерева в целом.

1. Treewidthlib: Тест для алгоритмов Treewidth и связанных с ним проблем с графами.
2. Реализация на C ++ использован в статье «Полный Алгоритм в любое время для Treewidth, Вибхав Гогейт и Рина Дечтер, UAI 2004. " Связь находится на домашней странице автора, где распространяются как исходный код LINUX, так и исполняемый файл Windows.
3. Реализация Hypertree Decomposition, используя несколько эвристик.
4. Инструмент панели инструментов имеет реализацию некоторой эвристики декомпозиции дерева.
5. Библиотека TreeD: имеет исходный код некоторых методов декомпозиции

Рекомендации

• Дехтер, Рина (2003). Обработка ограничений. Морган Кауфманн. ISBN  1-55860-890-7
• Дауни, Род; Майкл Феллоуз (1997). Параметризованная сложность. Springer. ISBN  0-387-94883-X
• Готтлоб, Георг; Никола Леоне; Франческо Скарчелло (2001). "Разложение гипердерева: обзор". MFCS 2001. С. 37–57.^{[мертвая ссылка ]}
• Готтлоб, Георг; Никола Леоне; Франческо Скарчелло (2000). «Сравнение методов структурной декомпозиции CSP». Искусственный интеллект. 124 (2): 243–282. Дои:10.1016 / S0004-3702 (00) 00078-3.