Разложение дерева - Tree decomposition

Граф с восемью вершинами и его древовидное разложение на дерево с шестью вершинами. Каждое ребро графа соединяет две вершины, перечисленные вместе в некотором узле дерева, и каждая вершина графа указана в узлах непрерывного поддерева дерева. Каждый узел дерева содержит не более трех вершин, поэтому ширина этого разбиения равна двум.

В теория графов, а разложение дерева является отображением график в дерево который можно использовать для определения ширина дерева графа и ускорить решение некоторых вычислительных задач на графе.

Древовидные декомпозиции также называют соединительные деревья, кликовые деревья, или присоединяться к деревьям; они играют важную роль в таких проблемах, как вероятностный вывод, удовлетворение ограничений, оптимизация запросов,^{[нужна цитата ]} и матричное разложение.

Концепция разложения дерева была первоначально введена Рудольф Халин  (1976 ). Позже это было открыто заново Нил Робертсон и Пол Сеймур  (1984 ) и с тех пор изучается многими другими авторами.^[1]

Определение

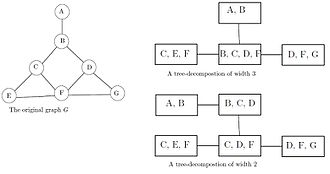
Интуитивно древовидная декомпозиция представляет вершины данного графа. г как поддеревья дерева, таким образом, что вершины в данном графе смежны только тогда, когда соответствующие поддеревья пересекаются. Таким образом, г образует подграф из граф пересечений поддеревьев. Полный граф пересечений - это хордовый граф.

Каждое поддерево связывает вершину графа с набором узлов дерева. Чтобы определить это формально, мы представляем каждый узел дерева как набор связанных с ним вершин. Таким образом, для данного графа г = (V, E), разложение дерева - это пара (Икс, Т), где Икс = {Икс₁, ..., Икс_п} - это семейство подмножеств (иногда называемых сумки) из V, и Т дерево, узлами которого являются подмножества Икс_я, удовлетворяющие следующим свойствам:^[2]

1. Объединение всех множеств Икс_я равно V. То есть каждая вершина графа связана по крайней мере с одним узлом дерева.
2. Для каждого ребра (v, ш) в графе существует подмножество Икс_я который содержит оба v и ш. То есть вершины смежны в графе только тогда, когда соответствующие поддеревья имеют общий узел.
3. Если Икс_я и Икс_j оба содержат вершину v, то все узлы Икс_k дерева на (уникальном) пути между Икс_я и Икс_j содержать v также. То есть узлы, связанные с вершиной v образуют связное подмножество Т. Это также известно как согласованность или свойство бегущего пересечения. Аналогично можно сказать, что если ${ displaystyle X_ {i}}$, ${ displaystyle X_ {j}}$ и ${ displaystyle X_ {k}}$ узлы, и ${ displaystyle X_ {k}}$ находится на пути от ${ displaystyle X_ {i}}$ к ${ displaystyle X_ {j}}$, тогда ${ displaystyle X_ {i} cap X_ {j} substeq X_ {k}}$.

Древовидная декомпозиция графа далеко не единственная; например, тривиальное разложение дерева содержит все вершины графа в его единственном корневом узле.

Разбиение дерева, в котором базовое дерево является граф путей называется разложением пути, а параметр ширины, полученный из этих специальных типов разложения дерева, известен как ширина пути.

Разложение дерева (Икс, Т = (я, F)) ширины дерева k является гладкий; плавный, если для всех ${ displaystyle i in I: | X_ {i} | = k + 1}$, и для всех ${ displaystyle (i, j) in F: | X_ {i} cap X_ {j} | = k}$.^[3]

Минимальное количество деревьев в разложении дерева - это номер дерева из Г.

Ширина дерева

Два разных древовидных разложения одного и того же графа

В ширина разложения дерева - это размер его наибольшего множества Икс_я минус один. В ширина дерева tw (г) графа г минимальная ширина среди всех возможных древовидных разложений г. В этом определении размер самого большого набора уменьшается на единицу, чтобы сделать ширину дерева равной единице. Ширина дерева также может быть определена из структур, отличных от древовидной декомпозиции, включая хордовые графы, ежевики, и убежища.

NP-полный, чтобы определить, г имеет ширину не более заданной переменной k.^[4]Однако когда k - любая фиксированная константа, графики с шириной дерева k можно распознать, а ширина k построенное для них разложение дерева за линейное время.^[3] Временная зависимость этого алгоритма от k экспоненциально.

Динамическое программирование

В начале 1970-х годов было замечено, что большой класс задач комбинаторной оптимизации, определенных на графах, может быть эффективно решен непоследовательными методами. динамическое программирование пока граф имел ограниченный измерение,^[5] параметр, связанный с шириной дерева. Позже несколько авторов независимо друг от друга наблюдали, в конце 1980-х годов,^[6] столько алгоритмических проблем, которые НП-полный для произвольных графов может быть эффективно решена динамическое программирование для графов с ограниченной древесной шириной, используя древовидные разложения этих графов.

В качестве примера рассмотрим задачу поиска максимальный независимый набор в графике ширины дерева k. Чтобы решить эту проблему, сначала произвольно выберите один из узлов разложения дерева в качестве корня. Для узла Икс_я разложения дерева, пусть D_я - объединение множеств Икс_j спускающийся с Икс_я. Для независимого набора S ⊂ Икс_я, позволять А(S,я) обозначают размер наибольшего независимого подмножества я из D_я такой, что я ∩ Икс_я = S. Аналогично для соседней пары узлов Икс_я и Икс_j, с участием Икс_я дальше от корня дерева, чем Икс_j, и независимый набор S ⊂ Икс_я ∩ Икс_j, позволять B(S,я,j) обозначают размер наибольшего независимого подмножества я из D_я такой, что я ∩ Икс_я ∩ Икс_j = S. Мы можем рассчитать эти А и B значения путем обхода дерева снизу вверх:

${ Displaystyle A (S, я) = | S | + сумма _ {j} влево (В (S cap X_ {j}, j, i) - | S cap X_ {j} | right) }$

${ Displaystyle B (S, я, j) ​​= max _ {S ' подмножество X_ {i} на вершине S = S' cap X_ {j}} A (S ', i)}$

где сумма в расчете ${ Displaystyle А (S, я)}$ находится над дочерними элементами узла ${ displaystyle X_ {i}}$.

На каждом узле или ребре не более 2^k наборы S для которого нам нужно вычислить эти значения, поэтому, если k является константой, тогда весь расчет занимает постоянное время для каждого ребра или узла. Размер максимального независимого набора - это наибольшее значение, хранящееся в корневом узле, а сам максимальный независимый набор может быть найден (как это стандартно в алгоритмах динамического программирования) путем обратного отслеживания этих сохраненных значений, начиная с этого наибольшего значения. Таким образом, в графах с ограниченной шириной дерева задача о максимальном независимом множестве может быть решена за линейное время. Подобные алгоритмы применимы ко многим другим задачам с графами.

Этот подход динамического программирования используется в машинное обучение через алгоритм дерева соединений для распространение веры в графах ограниченной ширины дерева. Он также играет ключевую роль в алгоритмах вычисления ширины дерева и построения декомпозиций дерева: обычно такие алгоритмы имеют первый шаг, который приблизительно ширина дерева, построение разложения дерева с этой приблизительной шириной, а затем второй шаг, который выполняет динамическое программирование в приблизительном разложении дерева для вычисления точного значения ширины дерева.^[3]

Смотрите также

• Ежевика и убежища - Два вида структур, которые можно использовать в качестве альтернативы древовидной декомпозиции при определении ширины дерева графа.
• Ветка-разложение - Тесно связанная структура, ширина которой находится в пределах постоянного множителя ширины дерева.
• Метод разложения - Древовидная декомпозиция используется в методе декомпозиции для решения проблемы удовлетворения ограничений.

Заметки

использованная литература