Сеть зависимости - Dependency network

В сеть зависимости подход обеспечивает системный анализ деятельности и топология направленных сети. Подход извлекает причинно-следственные связи между узлами сети (при анализе сетевой структуры) и обеспечивает важный шаг к выводу причинно-следственных связей между узлами сети (при анализе сетевой активности). Эта методология изначально была введена для изучения финансовых данных,^[1]^[2] он был расширен и применен к другим системам, таким как иммунная система,^[3] и семантические сети.^[4]

В случае сетевой активности анализ основан на частичные корреляции,^[5]^[6]^[7]^[8]^[9] которые становятся все более широко используемыми для исследования сложные системы. Проще говоря, частичная (или остаточная) корреляция является мерой эффекта (или вклада) данного узла, скажем j, на корреляции между другой парой узлов, скажем я и k. Используя эту концепцию, зависимость одного узла от другого вычисляется для всей сети. Это приводит к ориентированной взвешенной матрице смежности полностью подключенной сети. После построения матрицы смежности для построения сети можно использовать различные алгоритмы, такие как пороговая сеть, Минимальное связующее дерево (MST), Планарный график с максимальной фильтрацией (PMFG) и другие.

Сеть зависимостей финансовых данных для 300 акций S & P500, торгуемых в период 2001–2003 годов. Акции сгруппированы по секторам экономики, а стрелка указывает направление влияния. Хабом сети, наиболее влиятельным сектором, является финансовый сектор. Воспроизведение из Kenett et al., PLoS ONE 5 (12), e15032 (2010)

Важность

Сеть зависимостей на основе частичной корреляции - это класс корреляционной сети, способной обнаруживать скрытые связи между своими узлами.

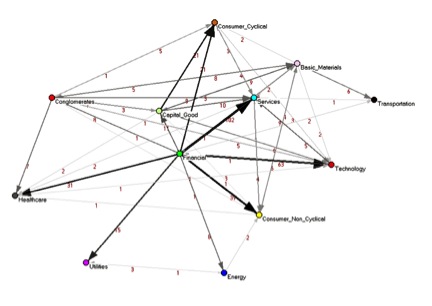
Эта оригинальная методика была впервые представлена в конце 2010 г. и опубликована в PLoS ONE.^[1] Они количественно раскрыли скрытую информацию о базовой структуре Фондовый рынок США, информация, отсутствующая в стандарте корреляция сети. Одним из основных результатов этой работы является то, что за исследуемый период времени (2001–2003 гг.) В структуре сети преобладали компании, принадлежащие финансовый сектор, которые являются узлы в сети зависимостей. Таким образом, они впервые смогли количественно показать отношения зависимости между разными секторы экономики. После этой работы методология сети зависимостей была применена к исследованию иммунная система,^[3] и семантические сети.^[4] Таким образом, эта методология применима к любому сложная система.

Сеть зависимости активности специфических антител, измеренная для группы матерей. Панель (а) представляет сеть зависимостей, а панель (б) - стандартную корреляционную сеть. Воспроизведение из Madi et al., Chaos 21, 016109 (2011)

Пример сети зависимостей ассоциаций, построенной из полной семантической сети. Воспроизведение из Kenett et al., PLoS ONE 6 (8): e23912 (2011)

Обзор

Чтобы быть более конкретным, частные корреляции пары, учитывая j есть корреляции между ними после правильного вычитания корреляций между я и j и между k и j. Определенная таким образом разница между корреляциями и частными корреляциями обеспечивает меру влияния узла j на корреляция. Таким образом, мы определяем влияние узла j на узле я, или зависимость узла я на узле j − D(я,j), чтобы быть суммой влияния узла j о соотношениях узла я со всеми остальными узлами.

В случае сетевой топологии анализ основан на влиянии удаления узла на кратчайшие пути между сетевые узлы. Более конкретно, мы определяем влияние узла j на каждой паре узлов (я, к) быть обратным топологическому расстоянию между этими узлами при наличии j минус обратное расстояние между ними при отсутствии узла j. Затем мы определяем влияние узла j на узле я, или зависимость узла я на узле j − D(я,j), чтобы быть суммой влияния узла j на расстояниях между узлами я со всеми другими узламиk.

Сети зависимости активности

Корреляции узел-узел

Корреляции узел-узел можно рассчитать следующим образом: Формула Пирсона:

{ Displaystyle C_ {я, j} = { гидроразрыва { left langle (X_ {i} (n) - mu _ {i}) (X_ {j} (n) - mu _ {j}) right rangle} { sigma _ {i} sigma _ {j}}}}

Где ${ Displaystyle X_ {я} (п)}$ и ${ Displaystyle X_ {j} (п)}$ активность узлов я и j предмета n, μ обозначает среднее, а сигма - стандартное отклонение профилей динамики узлов. я и j. Обратите внимание, что корреляции узел-узел (или для простоты корреляции узлов) для всех пар узлов определяют симметричную корреляционную матрицу, чья ${ displaystyle (я, j)}$ element - это соотношение между узлами я и j.

Частичные корреляции

Затем мы используем полученные корреляции узлов для вычисления частичных корреляций. Частичный коэффициент корреляции первого порядка - это статистическая мера, показывающая, как третья переменная влияет на корреляцию между двумя другими переменными. Частичная корреляция между узлами я и k относительно третьего узла ${ Displaystyle j-PC (я, к середина j)}$ определяется как:

{ Displaystyle ПК (я, к mid j) = { гидроразрыва {C (i, k) -C (i, j) C (k, j)} { sqrt {[1-C ^ {2} ( i, j)] [1-C ^ {2} (k, j)]}}}}

куда ${ Displaystyle С (я, j), С (я, к)}$ и ${ displaystyle C (j, k)}$ корреляции узлов, определенные выше.

Корреляционное влияние и корреляционная зависимость

Относительный эффект корреляций ${ Displaystyle C (я, j)}$ и ${ displaystyle C (j, k)}$ узла j о соотношении C(я,k) дан кем-то:

{ Displaystyle д (я, к середина j) эквив С (я, к) -PC (я, к | j)}

Это позволяет избежать тривиального случая, когда узел j похоже, сильно влияет на корреляцию ${ Displaystyle С (я, к)}$ , в основном потому, что ${ Displaystyle С (я, j), С (я, к)}$ и ${ displaystyle C (j, k)}$ имеют небольшие значения. Отметим, что эту величину можно рассматривать либо как корреляционную зависимость C(я,k) на узле j, (термин, используемый здесь) или как корреляционное влияние узла j о соотношении C(я,k).

Зависимости активности узла

Далее мы определяем общее влияние узла j на узле я, или зависимость D(я,j) узла я на узле j быть:

{ Displaystyle D (я, j) ​​= { гидроразрыва {1} {N-1}} sum _ {k neq j} ^ {N-1} d (i, k mid j)}

Как определено,D(я,j) - мера среднего влияния узла j о соотношениях С (я, к) по всем узлам k не равно j. Зависимости активности узла определяют матрицу зависимостей D чей (я,j) элемент является зависимостью узла я на узле j. Важно отметить, что хотя корреляционная матрица C является симметричной матрицей, матрица зависимостей D несимметрична - ${ Displaystyle D (я, j) neq D (j, я)}$ так как влияние узла j на узле я не равно влиянию узла я на узле j. По этой причине некоторые методы, используемые при анализе корреляционной матрицы (например, PCA), должны быть заменены или менее эффективны. Тем не менее, есть и другие методы, такие как те, что используются здесь, которые могут должным образом учесть несимметричный характер матрицы зависимостей.

Структура сети зависимости

Влияние пути и зависимость от расстояния: относительный эффект узла j по направленному пути ${ Displaystyle DP (я rightarrow k | j)}$ - кратчайший топологический путь с каждым сегментом соответствует расстоянию 1 между узлами я и k дано:

{ Displaystyle DP (я rightarrow k mid j) Equiv { frac {1} {td (i rightarrow k mid j ^ {+})}} - { frac {1} {td (i вправо k mid j ^ {-})}}}

куда ${ displaystyle td (я rightarrow k | j ^ {+})}$ и ${ displaystyle td (я rightarrow k mid j ^ {-})}$ - кратчайший направленный топологический путь от узла я узел k при наличии и отсутствии узла j соответственно.

Структурные зависимости узлов

Далее мы определяем общее влияние узла j на узле я, или зависимость D(я,j) узла я на узле j быть:

${ Displaystyle D (я, j) = { гидроразрыва {1} {N-1}} sum _ {k = 1} ^ {N-1} DP (я rightarrow k mid j)}$

Как определено, D(я,j) - мера среднего влияния узла j по направленным путям от узла я ко всем остальным узлам k. Структурные зависимости узла определяют матрицу зависимостей D чей (я,j) элемент является зависимостью узла я на узле j, или влияние узла j на узле я. Важно отметить, что матрица зависимостей D несимметрична - ${ Displaystyle D (я, j) neq D (j, я)}$ поскольку влияние узла j на узле я не равно влиянию узла я на узле j.

Визуализация сети зависимостей

Матрица зависимостей - это взвешенная матрица смежности, представляющая полностью подключенную сеть. Для фильтрации полностью подключенной сети для получения наиболее значимой информации могут применяться различные алгоритмы, например использование порогового подхода,^[1] или разные алгоритмы обрезки. Широко используемый метод построения информативного подграфа полной сети - это минимальное связующее дерево (MST).^[10]^[11]^[12]^[13]^[14] Другой информативный подграф, который сохраняет больше информации (по сравнению с MST), - это планарный график с максимальной фильтрацией (PMFG).^[15] который здесь используется. Оба метода основаны на иерархическая кластеризация и полученные подграфы включают все N узлы в сети, чьи края представляют собой наиболее релевантные корреляции ассоциаций. Подграф MST содержит ${ Displaystyle (N-1)}$ ребер без петель, в то время как подграф PMFG содержит ${ Displaystyle 3 (N-2)}$ края.

Смотрите также

внешняя ссылка

[PLoS1_2010-1] а ^б ^c Kenett, Dror Y .; Тумминелло, Микеле; Мади, Асаф; Гур-Гершгорен, Гитит; Mantegna, Rosario N .; Бен-Джейкоб, Эшель (20 декабря 2010 г.). Скалас, Энрико (ред.). «Доминирующая часть финансового сектора, выявленная частичным корреляционным анализом фондового рынка». PLOS ONE. 5 (12): e15032. Bibcode:2010PLoSO ... 515032K. Дои:10.1371 / journal.pone.0015032. ISSN 1932-6203. ЧВК 3004792. PMID 21188140.

[ICF_subbmited-2] Дрор Й. Кенетт, Йоаш Шапира, Гитит Гур-Гершгорен и Эшель Бен-Джейкоб (представлены), Анализ силы сплочения индекса фондового рынка США, Материалы Международной конференции по эконофизике 2011 г., Кавала, Греция

[Chaos_2011-3] а ^б Асаф Мади, Дрор И. Кенетт, Шаррон Брансбург-Забари, Йифат Мербл, Франсиско Дж. Кинтана, Стефано Боккалетти, Альфред И. Таубер, Ирун Р. Коэн и Эшель Бен-Джейкоб (2011), Анализ сетей антигенной зависимости раскрывает иммунную реорганизация системы между рождением и взрослой жизнью, Хаос 21, 016109

[PLoS1_2011_2-4] а ^б Kenett, Yoed N .; Kenett, Dror Y .; Бен-Джейкоб, Эшель; Фауст, Мириам (24 августа 2011 г.). Perc, Matjaz (ред.). «Глобальные и локальные особенности семантических сетей: данные из ментального лексикона иврита». PLOS ONE. 6 (8): e23912. Bibcode:2011PLoSO ... 623912K. Дои:10.1371 / journal.pone.0023912. ISSN 1932-6203. ЧВК 3161081. PMID 21887343.

[baba_2004-5] Кунихиро Баба, Ритель Шибата, Масааки Сибуя (2004), Частичная корреляция и условная корреляция как меры условной независимости, Aust New Zealand J Stat 46 (4): 657–774.

[shapira_2009-6] Йоаш Шапира, Дрор Й. Кенетт и Эшель Бен-Джейкоб (2009 г.), Эффект согласования индекса на корреляции фондового рынка, Журнал физики Б. т. 72, нет. 4. С. 657–669.

[PLosS1_2011-7] Kenett, Dror Y .; Шапира, Йоаш; Мади, Асаф; Брансбург-Забары, Шаррон; Гур-Гершгорен, Гитит; Бен-Джейкоб, Эшель (27 апреля 2011 г.). Скалас, Энрико (ред.). «Анализ силы сплоченности индекса показывает, что рынок США стал склонен к системным коллапсам с 2002 года». PLOS ONE. 6 (4): e19378. Bibcode:2011PLoSO ... 619378K. Дои:10.1371 / journal.pone.0019378. ISSN 1932-6203. ЧВК 3083438. PMID 21556323.

[PNAS_sub-8] Дрор Кенетт, Матиас Раддант, Томас Люкс и Эшель Бен-Джейкоб (представлены), Развитие единообразия и нестабильности на глобальном рынке, испытывающем стресс, PNAS

[strak_2006-9] Эран Старк, Ротем Дрори и Моше Абелес (2006), Частичный кросс-корреляционный анализ устраняет неоднозначность в кодировании множественных признаков движения, J Neurophysiol 95: 1966–1975

[mategna_1999-10] Росарио Н. Мантенья, Иерархическая структура финансовых рынков, Евро. Phys. J. B 11 (1), 193–197 (1999)

[11] Розарио Н. Мантенья, Computer Physics Communications 121–122, 153–156 (1999)

[12] Гильермо Дж. Ортега, Рафаэль Г. Сола и Хесус Пастор, Комплексный сетевой анализ данных ЭКоГ человека, Письма о неврологии 447 (2-3), 129–133 (2008)^{[постоянная мертвая ссылка ]}

[13] Микеле Тумминелло, Клаудиа Короннелло, Фабрицио Лилло, Сальваторе Миччише и Ррозарио Н. Мантенья, Связующие деревья и оценки надежности бутстрапа в сетях на основе корреляции [1]

[14] Дуглас Б. Уэст, Введение в теорию графов, под редакцией Прентис-Холла, Энглвуд Клиффс, Нью-Джерси, 2001

[15] Микеле Тумминелло, Томазо Асте, Тициана Ди Маттео и Розарио Н. Мантенья, Инструмент для фильтрации информации в сложных системах, PNAS 102 (30), 10421–10426 (2005)

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]