Частичная корреляция - Partial correlation

В теория вероятности и статистика, частичная корреляция измеряет степень ассоциация между двумя случайные переменные, с удаленным эффектом набора управляющих случайных величин. Если мы хотим выяснить, в какой степени существует числовая связь между двумя интересующими переменными, используя их коэффициент корреляции дам вводящие в заблуждение результаты если есть другой, сбивать с толку, переменная, которая численно связана с обеими интересующими переменными. Этой вводящей в заблуждение информации можно избежать, контролируя смешивающую переменную, которая выполняется путем вычисления частного коэффициента корреляции. Это и есть мотивация для включения других правых переменных в множественная регрессия; но в то время как множественная регрессия дает беспристрастный результаты для размер эффекта, он не дает числового значения меры силы взаимосвязи между двумя интересующими переменными.

Например, если у нас есть экономический данные о потреблении, доходе и богатстве различных людей, и мы хотим увидеть, существует ли связь между потреблением и доходом, неспособность контролировать богатство при вычислении коэффициента корреляции между потреблением и доходом может дать неверный результат, поскольку доход может численно относиться к богатству, которое, в свою очередь, может быть численно связано с потреблением; измеренная корреляция между потреблением и доходом может быть искажена этими другими корреляциями. Использование частичной корреляции позволяет избежать этой проблемы.

Как и коэффициент корреляции, частный коэффициент корреляции принимает значение в диапазоне от –1 до 1. Значение –1 передает идеальную отрицательную корреляцию, контролирующую некоторые переменные (то есть точную линейную зависимость, в которой более высокие значения одной переменной связаны с более низкими значениями другого); значение 1 передает идеальную положительную линейную зависимость, а значение 0 означает отсутствие линейной зависимости.

Частичная корреляция совпадает с условная корреляция если случайные величины совместно распределяемый как многомерный нормальный, Другой эллиптический, многомерный гипергеометрический, многомерный отрицательный гипергеометрический, полиномиальный или же Распределение Дирихле, но не иначе.^[1]

Формальное определение

Формально частичная корреляция между Икс и Y учитывая набор п управляющие переменные Z = {Z₁, Z₂, ..., Z_п}, написано ρ_XY·Z, это корреляция между остатки е_Икс и е_Y в результате линейная регрессия из Икс с Z и из Y с Z, соответственно. Частичная корреляция первого порядка (т. Е. Когда п = 1) - это разница между корреляцией и произведением устранимых корреляций, деленная на произведение коэффициентов отчуждения устранимых корреляций. В коэффициент отчуждения, и его связь с совместной дисперсией через корреляцию доступны в Guilford (1973, стр. 344–345).^[2]

Вычисление

Использование линейной регрессии

Простой способ вычислить частичную корреляцию выборки для некоторых данных - решить две связанные линейная регрессия задач, получить остатки и рассчитать корреляция между остатками. Позволять Икс и Y быть, как и выше, случайными величинами, принимающими действительные значения, и пусть Z быть п-мерная векторная случайная величина. Мы пишем Икс_я, у_я и z_я для обозначения яth из N i.i.d. наблюдения некоторых совместное распределение вероятностей над реальными случайными величинами Икс, Y и Z, с z_я был увеличен на 1, чтобы учесть постоянный член в регрессии. Решение задачи линейной регрессии сводится к нахождению (п+1) -мерные векторы коэффициентов регрессии ${ displaystyle mathbf {w} _ {X} ^ {*}}$ и ${ displaystyle mathbf {w} _ {Y} ^ {*}}$ такой, что

{ displaystyle mathbf {w} _ {X} ^ {*} = arg min _ { mathbf {w}} left { sum _ {i = 1} ^ {N} (x_ {i} - langle mathbf {w}, mathbf {z} _ {i} rangle) ^ {2} right }}

{ displaystyle mathbf {w} _ {Y} ^ {*} = arg min _ { mathbf {w}} left { sum _ {i = 1} ^ {N} (y_ {i} - langle mathbf {w}, mathbf {z} _ {i} rangle) ^ {2} right }}

с N количество наблюдений и ${ Displaystyle langle mathbf {ш}, mathbf {v} rangle}$ то скалярное произведение между векторами ш и v.

Остатки тогда

{ displaystyle e_ {X, i} = x_ {i} - langle mathbf {w} _ {X} ^ {*}, mathbf {z} _ {i} rangle}

{ displaystyle e_ {Y, i} = y_ {i} - langle mathbf {w} _ {Y} ^ {*}, mathbf {z} _ {i} rangle}

и образец частичный корреляция тогда дается обычная формула для выборочной корреляции, но между этими новыми полученный значения:

{ displaystyle { hat { rho}} _ {XY cdot mathbf {Z}} = { frac {N sum _ {i = 1} ^ {N} e_ {X, i} e_ {Y, i} - sum _ {i = 1} ^ {N} e_ {X, i} sum _ {i = 1} ^ {N} e_ {Y, i}} {{ sqrt {N sum _ { i = 1} ^ {N} e_ {X, i} ^ {2} - left ( sum _ {i = 1} ^ {N} e_ {X, i} right) ^ {2}}} ~ { sqrt {N sum _ {i = 1} ^ {N} e_ {Y, i} ^ {2} - left ( sum _ {i = 1} ^ {N} e_ {Y, i} справа) ^ {2}}}}}}

{ displaystyle = { frac {N sum _ {i = 1} ^ {N} e_ {X, i} e_ {Y, i}} {{ sqrt {N sum _ {i = 1} ^ { N} e_ {X, i} ^ {2}}} ~ { sqrt {N sum _ {i = 1} ^ {N} e_ {Y, i} ^ {2}}}}}.}.}

В первом выражении все три члена после знаков минус равны 0, так как каждый содержит сумму остатков от обыкновенный метод наименьших квадратов регресс.

Пример

Предположим, у нас есть следующие данные о трех переменных: Икс, Y, и Z:

Икс	Y	Z
2	1	0
4	2	0
15	3	1
20	4	1

Если мы вычислим Коэффициент корреляции Пирсона между переменными Икс и Y, результат будет примерно 0,970, а если вычислить частичную корреляцию между Икс и Y, используя приведенную выше формулу, находим частную корреляцию 0,919. Вычисления были выполнены с использованием R со следующим кодом.

> Икс = c(2,4,15,20)> Y = c(1,2,3,4)> Z = c(0,0,1,1)> мм1 = lm(Икс~Z)> res1 = мм1$остатки> мм2 = lm(Y~Z)> res2 = мм2$остатки> кор(res1,res2)[1] 0.919145> кор(Икс,Y)[1] 0.9695016> generalCorr::parcorMany(cbind(Икс,Y,Z))     nami namj partij partji rijMrji [1,] «X» «Y» «0,8844» «1» «-0,1156»[2,] «X» «Z» «0,1581» «1» «-0,8419»

Нижняя часть приведенного выше кода сообщает обобщенный нелинейный частный коэффициент корреляции между X и Y после удаления нелинейного эффекта Z, равный 0,8844. Также обобщенный частный коэффициент корреляции между X и Z после устранения нелинейного эффекта Y составляет 0,1581. Подробности смотрите в пакете R `generalCorr 'и его виньетках. Моделирование и другие подробности см. В Vinod (2017) «Обобщенная корреляция и причинная связь ядра с приложениями в экономике развития», Communications in Statistics - Simulation and Computing, vol. 46, [4513, 4534], доступно онлайн: 29 декабря 2015 г., URL https://doi.org/10.1080/03610918.2015.1122048.

Используя рекурсивную формулу

Решение задач линейной регрессии может быть дорогостоящим в вычислительном отношении. Собственно, пчастичная корреляция-го порядка (т. е. с |Z| = п) легко вычисляется из трех (п - 1) частные корреляции -го порядка. Частичная корреляция нулевого порядка ρ_{XY· Ø} определяется как регулярный коэффициент корреляции ρ_XY.

Это справедливо для любого ${ Displaystyle Z_ {0} in mathbf {Z},}$ который^{[нужна цитата ]}

{ displaystyle rho _ {XY cdot mathbf {Z}} = { frac { rho _ {XY cdot mathbf {Z} setminus {Z_ {0} }} - rho _ {XZ_ {0} cdot mathbf {Z} setminus {Z_ {0} }} rho _ {Z_ {0} Y cdot mathbf {Z} setminus {Z_ {0} }}} { { sqrt {1- rho _ {XZ_ {0} cdot mathbf {Z} setminus {Z_ {0} }} ^ {2}}} { sqrt {1- rho _ {Z_ { 0} Y cdot mathbf {Z} setminus {Z_ {0} }} ^ {2}}}}}.}.

Наивно реализуя это вычисление как рекурсивный алгоритм дает экспоненциальное время сложность. Однако это вычисление имеет перекрывающиеся подзадачи свойство, такое что использование динамическое программирование или просто кэширование результатов рекурсивных вызовов дает сложность ${ Displaystyle { mathcal {O}} (п ^ {3})}$ .

Обратите внимание, что в случае, когда Z - единственная переменная, это сводится к:^{[нужна цитата ]}

{ displaystyle rho _ {XY cdot Z} = { frac { rho _ {XY} - rho _ {XZ} rho _ {ZY}} {{ sqrt {1- rho _ {XZ} ^ {2}}} { sqrt {1- rho _ {ZY} ^ {2}}}}}}

Использование обращения матрицы

В ${ Displaystyle { mathcal {O}} (п ^ {3})}$ время другой подход позволяет все частичные корреляции, которые должны быть вычислены между любыми двумя переменными Икс_я и Икс_j набора V мощности п, учитывая все остальные, т.е. ${ Displaystyle mathbf {V} setminus {X_ {i}, X_ {j} }}$ , если корреляционная матрица Ω = (ρ_{Икс_яИкс_j}), является положительно определенный и поэтому обратимый. Если мы определим матрица точности п = (п_ij ) = Ω⁻¹, у нас есть:

{ displaystyle rho _ {X_ {i} X_ {j} cdot mathbf {V} setminus {X_ {i}, X_ {j} }} = - { frac {p_ {ij}} { sqrt {p_ {ii} p_ {jj}}}}.}

Интерпретация

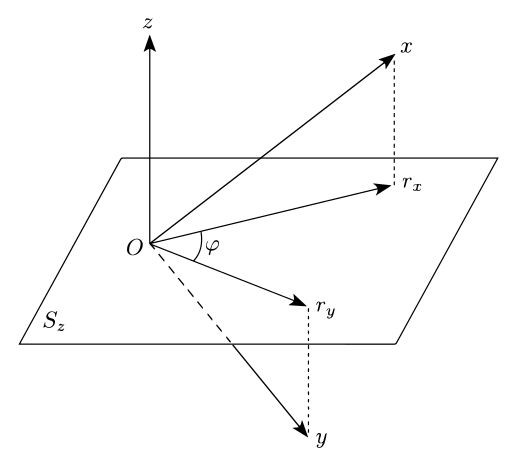
Геометрическая интерпретация частичной корреляции для случая N = 3 наблюдения и, таким образом, двумерная гиперплоскость

Геометрический

Пусть три переменные Икс, Y, Z (куда Z является "контрольной" или "дополнительной переменной") выбирается из совместного распределения вероятностей по п переменные V. Далее пусть v_я, 1 ≤ я ≤ N, быть N п-размерный i.i.d. наблюдения, взятые из совместного распределения вероятностей по V. Затем мы рассматриваем N-мерные векторы Икс (формируется последовательными значениями Икс над наблюдениями), у (формируется значениями Y) и z (формируется значениями Z).

Можно показать, что остатки е_{X, я} исходя из линейной регрессии Икс на Z, если также рассматривать как N-мерный вектор е_Икс (обозначен р_Икс на прилагаемом графике) имеют нулевой скалярное произведение с вектором z создано Z. Это означает, что вектор невязок лежит на (N–1) -мерный гиперплоскость S_z то есть перпендикуляр к z.

То же самое относится и к остаткам е_{Y, я} создание вектора е_Y. Тогда желаемая частичная корреляция косинус угла φ между прогнозы е_Икс и е_Y из Икс и усоответственно на гиперплоскость, перпендикулярную z.^[3]^{:гл. 7}

Как критерий условной независимости

При условии, что все задействованные переменные многомерный гауссовский, частичная корреляция ρ_XY·Z равен нулю тогда и только тогда, когда Икс является условно независимый из Y данный Z.^[1]В общем случае это свойство не выполняется.

К тест если выборочная частичная корреляция ${ displaystyle { hat { rho}} _ {XY cdot mathbf {Z}}}$ подразумевает истинную частичную корреляцию населения, равную 0, коэффициент Фишера z-преобразование частичной корреляции может быть использован:

{ displaystyle z ({ hat { rho}} _ {XY cdot mathbf {Z}}) = { frac {1} {2}} ln left ({ frac {1 + { hat { rho}} _ {XY cdot mathbf {Z}}} {1 - { hat { rho}} _ {XY cdot mathbf {Z}}}} right).}

В нулевая гипотеза является ${ displaystyle H_ {0}: rho _ {XY cdot mathbf {Z}} = 0}$ , для тестирования против альтернативы с двумя хвостами ${ displaystyle H_ {A}: rho _ {XY cdot mathbf {Z}} neq 0}$ . Мы отвергаем ЧАС₀ с уровень значимости α если:

{ displaystyle { sqrt {N- | mathbf {Z} | -3}} cdot | z ({ hat { rho}} _ {XY cdot mathbf {Z}}) |> Phi ^ {-1} (1- alpha / 2),}

где Φ (·) - кумулятивная функция распределения из Гауссово распределение с нуля иметь в виду и единица стандартное отклонение, и N это размер образца. Этот z-преобразование является приблизительным, и фактическое распределение выборочного (частичного) коэффициента корреляции не является прямым. Однако точный t-тест на основе комбинации коэффициента частичной регрессии, частичного коэффициента корреляции и частичной дисперсии доступны.^[4]

Распределение выборочной частичной корреляции было описано Фишером.^[5]

Частичная корреляция (частичная корреляция)

Статистика частичной (или частичной) корреляции аналогична статистике частичной корреляции. Оба сравнивают вариации двух переменных после контроля определенных факторов, но для расчета полупчастичной корреляции третья переменная остается постоянной для любого Икс или же Y но не обоих, тогда как для частичной корреляции третья переменная остается постоянной для обоих.^[6] Полупарциальная корреляция сравнивает уникальную вариацию одной переменной (без удаления вариации, связанной с Z переменная (и)) с нефильтрованной вариацией другой, в то время как частичная корреляция сравнивает уникальную вариацию одной переменной с уникальной вариацией другой.

Полупарциальная (или частичная) корреляция может рассматриваться как более актуальная с практической точки зрения, «потому что она масштабируется (т. Е. Относительно) общей изменчивости в зависимой (ответной) переменной».^[7] И наоборот, он менее полезен с теоретической точки зрения, поскольку менее точен в отношении роли уникального вклада независимой переменной.

Абсолютное значение получастичной корреляции Икс с Y всегда меньше или равно частичной корреляции Икс с Y. Причина в следующем: предположим, что соотношение Икс с Z был удален из Икс, давая остаточный вектор е_Икс . При вычислении частичной корреляции Y все еще содержит как уникальную дисперсию, так и дисперсию из-за ее связи с Z. Но е_Икс , будучи некоррелированным с Z, может объяснить только часть уникальной части дисперсии Y а не часть, связанная с Z. Напротив, при частичной корреляции только е_у (часть дисперсии Y это не связано с Z) требует объяснения, поэтому существует меньшая вариация типа, который е_Икс не могу объяснить.

Использование в анализе временных рядов

В анализ временных рядов, то частичная автокорреляционная функция (иногда «частичная корреляционная функция») временного ряда, для запаздывания час, так как

{ Displaystyle varphi (h) = rho _ {X_ {0} X_ {h} , cdot , {X_ {1}, , dots ,, X_ {h-1} }} .}

Эта функция используется для определения соответствующей длины лага для авторегрессия.

Смотрите также

внешняя ссылка

Прохоров, А. (2001) [1994], «Коэффициент частичной корреляции», Энциклопедия математики, EMS Press
Математические формулы в разделе «Описание» Подпрограмма PCORR из цифровой библиотеки IMSL
А пример с тремя переменными

[Baba-1] а ^б Баба, Кунихиро; Ритеи Шибата; Масааки Сибуя (2004). «Частичная корреляция и условная корреляция как меры условной независимости». Статистический журнал Австралии и Новой Зеландии. 46 (4): 657–664. Дои:10.1111 / j.1467-842X.2004.00360.x.

[2] Гилфорд Дж. П., Фрухтер Б. (1973). Фундаментальная статистика в психологии и образовании. Токио: Макгроу-Хилл Когакуша, ООО.

[3] Раммель, Р. Дж. (1976). «Понимание корреляции».

[4] Кендалл MG, Стюарт А. (1973) Расширенная теория статистики, Том 2 (3-е издание), ISBN 0-85264-215-6, Раздел 27.22

[5] Фишер, Р.А. (1924). «Распределение частного коэффициента корреляции». Метрон. 3 (3–4): 329–332.

[6] ttps://web.archive.org/web/20140206182503/http://luna.cas.usf.edu/~mbrannic/files/regression/Partial.html. Архивировано из оригинал на 2014-02-06. Отсутствует или пусто | название = (помощь)

[7] StatSoft, Inc. (2010). «Частичная (или частичная) корреляция», Электронный учебник статистики. Талса, OK: StatSoft, по состоянию на 15 января 2011 г.

[1]

[2]

[3]

[4]

[5]

[6]

[7]