График Q – Q - Википедия - Q–Q plot

Нормальный график Q – Q случайно сгенерированного независимого стандарта экспоненциальный данные, (

Икс ~ Опыт (1)

). Этот график Q – Q сравнивает образец из данные по вертикальной оси до статистическая совокупность по горизонтальной оси. Точки следуют сильно нелинейному шаблону, предполагая, что данные не распределяются как стандартное нормальное (

Икс ~ N (0,1)

). Смещение между линией и точками предполагает, что среднее значение данных не 0. Медиана точек может быть определена как около 0,7.

Нормальный график Q – Q, сравнивающий случайно сгенерированные, независимые стандартные нормальные данные на вертикальной оси со стандартной нормальной совокупностью на горизонтальной оси. Линейность точек предполагает, что данные распределены нормально.

График Q – Q выборки данных по сравнению с Распределение Вейбулла. Децили распределений показаны красным. В верхней части диапазона очевидны три выброса. В остальном данные хорошо соответствуют модели Вейбулла (1,2).

График Q – Q, сравнивающий распределения стандартизированный суточные максимальные температуры на 25 станциях в американском штате Огайо в марте и июле. Изогнутый узор предполагает, что центральный квантили расположены более близко в июле, чем в марте, и что июльское распределение перекошенный слева по сравнению с мартовским распределением. Данные охватывают период 1893–2001 гг.

В статистике График Q – Q (квантиль-квантиль) вероятностный график, который графический метод для сравнения двух распределения вероятностей замышляя их квантили друг против друга.^[1] Сначала выбирается набор интервалов для квантилей. Точка $(Икс, у)$ на графике соответствует одному из квантилей второго распределения ( $у$ -координата), построенная против того же квантиля первого распределения ( $Икс$ -координат). Таким образом, линия представляет собой параметрическую кривую с параметром, который является номером интервала для квантиля.

Если два сравниваемых распределения похожи, точки на графике Q – Q будут примерно лежать на линии $у = Икс$ . Если распределения связаны линейно, точки на графике Q – Q будут примерно лежать на одной линии, но не обязательно на прямой. $у = Икс$ . Графики Q – Q также можно использовать в качестве графического средства оценки параметров в семья в масштабе местности раздач.

График Q – Q используется для сравнения форм распределений, обеспечивая графическое представление того, как такие свойства, как место расположения, шкала, и перекос похожи или разные в двух дистрибутивах. Графики Q – Q можно использовать для сравнения наборов данных или теоретические распределения. Использование графиков Q – Q для сравнения двух выборок данных можно рассматривать как непараметрический подход к сравнению их основных распределений. График Q – Q, как правило, является более действенным подходом для этого, чем обычный метод сравнения гистограммы из двух образцов, но для интерпретации требуется больше навыков. Графики Q – Q обычно используются для сравнения набора данных с теоретической моделью.^[2]^[3] Это может обеспечить графическую оценку «степени соответствия», а не сводку к числовой сводке. Графики Q – Q также используются для сравнения двух теоретических распределений друг с другом.^[4] Поскольку графики Q – Q сравнивают распределения, нет необходимости наблюдать значения в виде пар, как в диаграмма рассеяния, или даже для того, чтобы количество значений в двух сравниваемых группах было одинаковым.

Термин «вероятностный график» иногда относится конкретно к графику Q – Q, иногда к более общему классу графиков, а иногда к менее часто используемым. График P – P. В график вероятности график коэффициента корреляции (График PPCC) - величина, полученная из идеи графиков Q – Q, которая измеряет соответствие подобранного распределения наблюдаемым данным и иногда используется как средство подгонки распределения к данным.

Определение и конструкция

График Q – Q для дат первого открытия / последнего закрытия Маршрут штата Вашингтон 20, по сравнению с нормальным распределением.^[5] Выбросы видны в правом верхнем углу.

А Q – Q график представляет собой график зависимости квантилей двух распределений друг от друга или график, основанный на оценках квантилей. Образец точек на графике используется для сравнения двух распределений.

Основным этапом построения графика Q – Q является расчет или оценка квантилей, которые необходимо построить. Если одна или обе оси на графике Q – Q основаны на теоретическом распределении с непрерывным кумулятивная функция распределения (CDF), все квантили определены однозначно и могут быть получены путем инвертирования CDF. Если теоретическое распределение вероятностей с прерывистой функцией CDF является одним из двух сравниваемых распределений, некоторые из квантилей могут не быть определены, поэтому можно построить интерполированный квантиль. Если график Q – Q основан на данных, используется несколько квантильных оценок. Правила формирования графиков Q – Q, когда квантили должны быть оценены или интерполированы, называются построение позиций.

Простой случай - это два набора данных одинакового размера. В этом случае, чтобы построить график Q – Q, нужно упорядочить каждый набор в порядке возрастания, затем объединить в пары и построить соответствующие значения. Более сложная конструкция - это случай, когда сравниваются два набора данных разного размера. Для построения графика Q – Q в этом случае необходимо использовать интерполированный квантильная оценка, чтобы можно было построить квантили, соответствующие одной и той же базовой вероятности.

Говоря более абстрактно,^[4] с учетом двух кумулятивных функций распределения вероятностей $F$ и $грамм$ , с ассоциированными квантильные функции $F -1$ и $грамм -1$ (обратная функция CDF - функция квантиля), график Q – Q рисует $q$ -й квантиль $F$ против $q$ -й квантиль $грамм$ для диапазона значений $q$ . Таким образом, график Q – Q представляет собой параметрическая кривая проиндексировано более [0,1] со значениями в реальной плоскости $р 2$ .

Интерпретация

Точки, нанесенные на график Q – Q, всегда не убывают, если смотреть слева направо. Если два сравниваемых распределения идентичны, график Q – Q следует линии под углом 45 °. $у = Икс$ . Если два распределения согласуются после линейного преобразования значений в одном из распределений, то график Q – Q следует некоторой линии, но не обязательно линии $у = Икс$ . Если общий тренд графика Q – Q более пологий, чем линия $у = Икс$ , распределение по горизонтальной оси больше рассредоточенный чем распределение, нанесенное на вертикальную ось. И наоборот, если общий тренд графика Q – Q круче, чем линия $у = Икс$ , распределение по вертикальной оси больше рассредоточенный чем распределение, нанесенное на горизонтальную ось. Графики Q – Q часто имеют дугообразную или S-образную форму, что указывает на то, что одно из распределений более искажено, чем другое, или что одно из распределений имеет более тяжелые хвосты, чем другое.

Хотя график Q – Q основан на квантилях, на стандартном графике Q – Q невозможно определить, какая точка на графике Q – Q определяет данный квантиль. Например, невозможно определить медианное значение какого-либо из двух сравниваемых распределений, просматривая график Q – Q. На некоторых графиках Q – Q указаны децили, позволяющие сделать такие определения возможными.

Пересечение и наклон линейной регрессии между квантилями дает меру относительного местоположения и относительного масштаба выборок. Если медиана распределения, нанесенная на горизонтальную ось, равна 0, точка пересечения линии регрессии является мерой местоположения, а наклон - мерой масштаба. Расстояние между медианами - еще одна мера относительного местоположения, отраженная на графике Q – Q. "коэффициент корреляции графика вероятности "(График PPCC) - коэффициент корреляции между парными квантилями выборки. Чем ближе коэффициент корреляции к единице, тем ближе распределения к смещенным масштабированным версиям друг друга. Для распределений с одним параметром формы график коэффициента корреляции вероятностного графика предоставляет метод оценки параметра формы - один просто вычисляет коэффициент корреляции для разных значений параметра формы и использует тот, который лучше всего подходит, как если бы сравнивали раздачи разных типов.

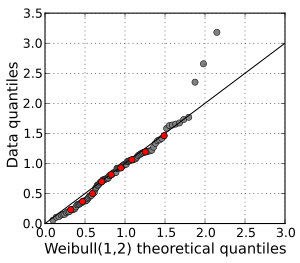
Другое распространенное использование графиков Q – Q - сравнение распределения выборки с теоретическим распределением, таким как стандартное нормальное распределение $N (0,1)$ , как в график нормальной вероятности. Как и в случае сравнения двух выборок данных, один упорядочивает данные (формально вычисляет статистику порядка), а затем наносит их на график относительно определенных квантилей теоретического распределения.^[3]

Построение позиций

Выбор квантилей из теоретического распределения может зависеть от контекста и цели. Один выбор, учитывая размер выборки $п$ , является $k / п$ за $k = 1, \dots, п$ , поскольку это квантили, которые реализует выборочное распределение. Последний из них, $п / п$ , соответствует 100-му процентилю - максимальному значению теоретического распределения, которое иногда бывает бесконечным. Другой вариант - использование $(k - 0.5) / п$ или вместо этого равномерно распределить точки в равномерном распределении, используя $k / (п + 1)$ .^[6]

Было предложено множество других вариантов, как формальных, так и эвристических, на основе теории или моделирования, актуальных в контексте. В следующих подразделах обсуждаются некоторые из них. Более узкий вопрос - это выбор максимума (оценка максимума совокупности), известного как Проблема с немецким танком, для которых существуют аналогичные решения типа "максимум выборки плюс пробел", проще всего $м + м / п - 1$ . Более формальное применение этого унифицированного интервала происходит в оценка максимального интервала параметров.

Ожидаемое значение статистики заказов для равномерного распределения

В $k / (п + 1)$ подход равняется построению точек в соответствии с вероятностью того, что последний из ( $п + 1$ ) случайно выбранные значения не будут превышать $k$ -й наименьший из первых $п$ случайно выбранные значения.^[7]^[8]

Ожидаемое значение статистики порядка для стандартного нормального распределения

При использовании график нормальной вероятности, используемые квантили ранки, квантиль ожидаемого значения статистики порядка стандартного нормального распределения.

В более общем смысле, Тест Шапиро-Уилка использует ожидаемые значения статистики заказов данного распределения; полученный график и линия дают обобщенный метод наименьших квадратов оценка местоположения и масштаба (из перехватить и склон подогнанной линии).^[9]Хотя это не слишком важно для нормального распределения (местоположение и масштаб оцениваются по среднему и стандартному отклонению соответственно), это может быть полезно для многих других распределений.

Однако это требует вычисления ожидаемых значений статистики порядка, что может быть затруднено, если распределение не является нормальным.

Медиана статистики заказа

В качестве альтернативы можно использовать оценки медиана статистики порядка, которую можно вычислить на основе оценок медианы статистики порядка равномерного распределения и квантильной функции распределения; это было предложено (Филлибен 1975 ).^[9]

Это может быть легко сгенерировано для любого распределения, для которого может быть вычислена функция квантиля, но, наоборот, результирующие оценки местоположения и масштаба больше не являются точными оценками наименьших квадратов, хотя они значительно различаются только для $п$ маленький.

Эвристика

Несколько различных формул были использованы или предложены в качестве аффинный симметричный построение позиций. Такие формулы имеют вид $(k - а) / (п + 1 - 2 а)$ за некоторую стоимость $а$ в диапазоне от 0 до 1, что дает диапазон между $k / (п + 1)$ и $(k - 1) / (п - 1)$ .

Выражения включают:

$k / (п + 1)$
$(k - 0.3) / (п + 0.4)$ .^[10]
$(k - 0.3175) / (п + 0.365)$ .^[11]^{[примечание 1]}
$(k - 0.326) / (п + 0.348)$ .^[12]
$(k - ⅓) / (п + ⅓)$ .^{[заметка 2]}
$(k - 0.375) / (п + 0.25)$ .^{[заметка 3]}
$(k - 0.4) / (п + 0.2)$ .^[13]
$(k - 0.44) / (п + 0.12)$ .^{[примечание 4]}
$(k - 0.5) / (п)$ .^[14]
$(k - 0.567) / (п - 0.134)$ .^[15]
$(k - 1) / (п - 1)$ .^{[примечание 5]}

Для большого размера выборки $п$ , между этими различными выражениями мало различий.

Оценка Филлибена

Статистические медианы порядка - это медианы статистика заказов распределения. Они могут быть выражены через функцию квантиля и статистические медианы порядка для непрерывного равномерного распределения к:

{ Displaystyle N (я) = G (U (я))}

куда $U (я)$ являются медианными статистическими значениями единого порядка и $грамм$ - функция квантиля для желаемого распределения. Функция квантиля обратна кумулятивная функция распределения (вероятность того, что $Икс$ меньше или равно некоторому значению). То есть, учитывая вероятность, нам нужен соответствующий квантиль кумулятивной функции распределения.

Джеймс Дж. Филлибен (Филлибен 1975 ) использует следующие оценки для медиан статистических данных единого порядка:

{ displaystyle m (i) = { begin {cases} 1-0,5 ^ {1 / n} & i = 1 { dfrac {i-0,3175} {n + 0,365}} & i = 2,3, ldots, n-1 0,5 ^ {1 / n} & i = n. end {case}}}

Причина такой оценки заключается в том, что статистические медианы порядка не имеют простой формы.

Смотрите также

Пробит анализ был разработан Честер Иттнер Блисс в 1934 г.

Примечания

^ Обратите внимание, что здесь также используется другое выражение для первой и последней точек. [1] цитирует оригинальную работу (Филлибен 1975 ). Это выражение является оценкой медианы из $U (k)$ .
^ Простая (и легко запоминающаяся) формула для построения позиций; используется в BMDP статистический пакет.
^ Это (Блом 1958 ) И является выражением, используемым в MINITAB.
^ Это положение на графике было использовано Ирвингом И. Грингортеном (Грингортен (1963)) для построения точек в тестах для Гамбель раздача.
^ Использован Филлибен (1975), эти точки построения равны режимы из $U (k)$ .

внешняя ссылка

График вероятности
Альтернативное описание QQ-графика: http://www.stats.gla.ac.uk/steps/glossary/probability_distributions.html#qqplot

[12] Обратите внимание, что здесь также используется другое выражение для первой и последней точек. [1] цитирует оригинальную работу (Филлибен 1975 ). Это выражение является оценкой медианы из $U (k)$ .

[14] Простая (и легко запоминающаяся) формула для построения позиций; используется в BMDP статистический пакет.

[15] Это (Блом 1958 ) И является выражением, используемым в MINITAB.

[17] Это положение на графике было использовано Ирвингом И. Грингортеном (Грингортен (1963)) для построения точек в тестах для Гамбель раздача.

[20] Использован Филлибен (1975), эти точки построения равны режимы из $U (k)$ .

[1] Wilk, M.B .; Gnanadesikan, R. (1968), "Методы построения вероятностных графиков для анализа данных", Биометрика, Biometrika Trust, 55 (1): 1–17, Дои:10.1093 / biomet / 55.1.1, JSTOR 2334448, PMID 5661047.

[2] Gnanadesikan (1977) p199.

[thode21-3] а ^б (Тоде 2002, Раздел 2.2.2, Графики квантилей-квантилей, п. 21 год )

[gibbons-4] а ^б (Гиббонс и Чакраборти 2003, п. 144 )

[closure-5] «SR 20 - North Cascades Highway - История открытия и закрытия». Перевалы Северных каскадов. Департамент транспорта штата Вашингтон. Октябрь 2009 г.. Получено 8 февраля 2009.

[6] Вейбулл, Валодди (1939), «Статистическая теория прочности материалов», IVA Handlingar, Шведская королевская академия инженерных наук (№ 151)

[7] Madsen, H.O .; и другие. (1986), Методы конструктивной безопасности

[8] Макконен, Л. (2008), "Завершение разногласий по поводу позиции построения графика", Коммуникации в статистике - теория и методы (37): 460–467

[thode31-9] а ^б Проверка на нормальность, Генри К. Тоде, CRC Press, 2002, ISBN 978-0-8247-9613-6, п. 31 год

[10] Бенар и Бос-Левенбах (1953). Нанесение наблюдений на вероятностную бумагу. Statistica Neederlandica, 7: 163-173. Дои:10.1111 / j.1467-9574.1953.tb00821.x. (на голландском)}

[11] Справочник по инженерной статистике: График нормальной вероятности

[13] Положение для построения графика без распространения, Ю и Хуанг

[16] Кунан (1978).

[18] Хазен, Аллен (1914), «Хранение в водохранилищах для городского водоснабжения», Сделки Американского общества инженеров-строителей (№ 77): 1547–1550

[19] Ларсен, смородина и охота (1980).

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[примечание 1]

[12]

[заметка 2]

[заметка 3]

[13]

[примечание 4]

[14]

[15]

[примечание 5]