Образец (статистика) - Sample (statistics)
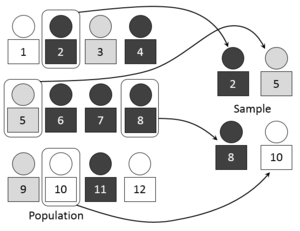
В статистика и количественные исследования методология, образец представляет собой набор людей или объектов, собранных или выбранных из статистическая совокупность в установленном порядке.[1] Элементы выборки известны как точки отбора проб, единицы выборки или наблюдения.[нужна цитата ] Задуманный как набор данных, образец часто обозначается заглавной буквой. римские буквы такой и , с его элементами, выраженными в нижнем регистре (например, ) и размер выборки обозначается буквой .[2][3]
Обычно популяция очень большая, поэтому перепись или полный перечисление всех людей в популяции либо непрактично, либо невозможно. Выборка обычно представляет собой подмножество управляемого размера. Образцы собираются и статистика рассчитываются по образцам, так что можно сделать выводы или же экстраполяции от выборки к генеральной совокупности.
Выборка может быть взята из совокупности без замены (т.е. ни один элемент не может быть выбран более одного раза в одном и том же образце), и в этом случае это подмножество из численность населения; или же с заменой (т.е. элемент может появляться несколько раз в одном образце), и в этом случае это мультиподмножество.[4]
Виды образцов
А полный образец представляет собой набор объектов из родительской популяции, который включает все такие объекты, которые удовлетворяют ряду четко определенных критериев выбора.[5][неудачная проверка ] Например, полная выборка австралийских мужчин ростом выше 2 м будет состоять из списка каждый Самец-австралиец выше 2 м. Но сюда не входят немецкие мужчины, высокие австралийские женщины или люди ростом ниже 2 м. Поэтому для составления такой полной выборки требуется полный список родительского населения, включая данные о росте, поле и национальности для каждого члена этого родительского населения. В случае человеческих популяций такой полный список вряд ли существует (человеческая популяция исчисляется миллиардами). Но такие полные образцы часто доступны в других дисциплинах, таких как набор игроков в крупной спортивной лиге, даты рождения членов парламента или полный ограниченный по величине список астрономических объектов.
An объективная (репрезентативная) выборка представляет собой набор объектов, выбранных из полной выборки с использованием процесса выбора, который не зависит от свойств объектов.[6] Например, объективная выборка австралийских мужчин ростом выше 2 м может состоять из случайной выборки из 1% австралийских мужчин ростом выше 2 м. Но человек, выбранный из списка избирателей, может оказаться непредвзятым, поскольку, например, мужчины в возрасте до 18 лет не будут включены в список избирателей. В астрономическом контексте объективная выборка может состоять из той части полной выборки, для которой доступны данные, при условии, что доступность данных не зависит от свойств отдельных источников.
Лучший способ избежать предвзятой или нерепрезентативной выборки - выбрать случайный пример, также известный как вероятностная выборка. Случайная выборка определяется как выборка, в которой каждый отдельный член совокупности имеет известный ненулевой шанс быть выбранным в качестве части выборки.[7] Есть несколько типов случайных выборок. простые случайные выборки, систематические образцы, стратифицированные случайные выборки, и кластерные случайные выборки.
Выборка, которая не является случайной, называется неслучайная выборка или не вероятностная выборка.[8] Некоторые примеры неслучайных выборок: удобные образцы, образцы суждения, целевые образцы, образцы квот, образцы снежков, и квадратурные узлы в квази-Монте-Карло методы.
Математическое описание случайной выборки
С математической точки зрения, учитывая распределение вероятностей F, случайная выборка длины п (куда п может быть любым положительным целым числом) представляет собой набор реализаций п независимый, одинаково распределенные (iid ) случайные величины с распределением F.[9]
Образец конкретно представляет результаты п эксперименты, в которых измеряется одна и та же величина. Например, если мы хотим оценить средний рост представителей определенной популяции, мы измеряем рост п лиц. Каждое измерение берется из распределения вероятностей F характеризуя популяцию, поэтому каждый измеренный рост есть реализация случайной величины с распределением F. Обратите внимание, что набор случайных величин (т. Е. Набор измеримых функций) не следует путать с реализациями этих переменных (которые являются значениями, которые принимают эти случайные величины). Другими словами, - функция, представляющая измерение на я-й эксперимент, и это значение, полученное при измерении.
Смотрите также
- Теория оценок
- Репликация (статистика)
- Определение размера выборки
- Смещение выборки
- Выборочное распределение
- Ошибка выборки
- Выборка (статистика)
- Выборка опроса
Примечания
- ^ Пек, Рокси; Олсен, Крис и Девор, Джей (2008), Введение в статистику и анализ данных (3-е изд.), Belmont, Cal .: Thomson Brooks / Cole, p. 8, ISBN 978-0-495-11873-2, LCCN 2006933904, получено 2009-08-04
- ^ «Список вероятностных и статистических символов». Математическое хранилище. 2020-04-26. Получено 2020-08-21.
- ^ "Что означает размер выборки?". Наука. Получено 2020-08-21.
- ^ Borzyszkowski, Andrzej M .; Соколовский, Стефан, ред. (1993), «Характеристика морфизмов Штурма» (PDF), Математические основы информатики 1993. 18-й Международный симпозиум, MFCS'93, Гданьск, Польша, 30 августа - 3 сентября 1993 г. Труды, Конспект лекций по информатике, 711, стр. 281–290, CiteSeerX 10.1.1.361.7021, Дои:10.1007/3-540-57182-5_20, ISBN 978-3-540-57182-7, Zbl 0925.11026
- ^ Пратт, Дж. У., Райффа, Х. и Шайфер, Р. (1995). Введение в статистическую теорию принятия решений. Кембридж, Массачусетс: MIT Press. ISBN 9780262161442. МИСТЕР1326829
- ^ Ломакс, Р. Г. и Хас-Воган, Дебби Л. Введение в статистические концепции (3-е изд.).
- ^ Кокран, Уильям Г. (1977). Методы отбора проб (Третье изд.). Вайли. ISBN 978-0-471-16240-7.
- ^ Йохан Стридом (2005). Введение в маркетинг (Третье изд.). Вайли. ISBN 978-0-471-16240-7.
- ^ Сэмюэл С. Уилкс, Математическая статистика, Джон Вили, 1962, Раздел 8.1.







