Факторный эксперимент - Википедия - Factorial experiment
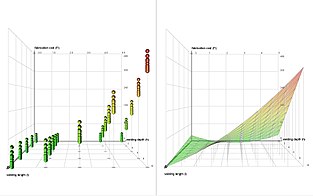
В статистика, полный факторный эксперимент представляет собой эксперимент, план которого состоит из двух или более факторов, каждый из которых имеет дискретные возможные значения или «уровни», и чей экспериментальные единицы взять на себя все возможные комбинации этих уровней с учетом всех таких факторов. Полный факторный план можно также назвать полностью пересеченный дизайн. Такой эксперимент позволяет исследователю изучить влияние каждого фактора на переменная ответа, а также эффекты взаимодействия между факторами переменной ответа.
В подавляющем большинстве факторных экспериментов каждый фактор имеет только два уровня. Например, с двумя факторами, каждый из которых принимает два уровня, факторный эксперимент будет иметь в общей сложности четыре комбинации лечения и обычно называется Факторный дизайн 2 × 2.
Если количество комбинаций в полном факторном плане слишком велико, чтобы быть осуществимым с точки зрения логистики, дробный факторный план может быть сделано, в котором некоторые из возможных комбинаций (обычно не менее половины) опускаются.
История
Факториальные дизайны использовались в 19 веке Джон Беннет Лоз и Джозеф Генри Гилберт из Экспериментальная станция Ротамстед.[1]
Рональд Фишер В 1926 г. утверждал, что «сложные» планы (такие как факторные планы) более эффективны, чем изучение одного фактора за раз.[2] Фишер писал:
«Ни один из афоризмов не повторяется чаще в связи с полевыми испытаниями, чем то, что мы должны задавать природе несколько вопросов или, в идеале, по одному вопросу за раз. Автор убежден, что это мнение полностью ошибочно».
По его мнению, природа лучше всего ответит на «логичный и тщательно продуманный вопросник». Факторный план позволяет определить влияние нескольких факторов и даже взаимодействия между ними с помощью того же количества испытаний, которое необходимо для определения любого из эффектов отдельно с той же степенью точности.
Фрэнк Йейтс внесли значительный вклад, особенно в анализ конструкций, благодаря Анализ Йетса.
Термин «факториал», возможно, не использовался в печати до 1935 года, когда Фишер использовал его в своей книге. План экспериментов.[3]
Преимущества факторных экспериментов
Многие люди исследуют влияние только одного фактора или переменной. По сравнению с такими однофакторными экспериментами (OFAT) факторные эксперименты предлагают несколько преимуществ.[4][5]
- Факторные планы более эффективны, чем эксперименты OFAT. Они предоставляют больше информации по аналогичной или более низкой цене. Они могут находить оптимальные условия быстрее, чем эксперименты OFAT.
- Факторные планы позволяют исследовать дополнительные факторы без дополнительных затрат.
- Когда эффект одного фактора отличается для разных уровней другого фактора, его нельзя обнаружить с помощью плана эксперимента OFAT. Для обнаружения таких взаимодействия. Использование OFAT при наличии взаимодействия может привести к серьезному непониманию того, как реакция меняется в зависимости от факторов.
- Факторные планы позволяют оценить влияние одного фактора на нескольких уровнях других факторов, давая выводы, которые действительны для ряда экспериментальных условий.
Пример преимуществ факторных экспериментов
В своей книге Улучшение почти всего: идеи и эссе, статистик Джордж Бокс дает много примеров преимуществ факторных экспериментов. Вот один.[6] Инженеры производителя подшипников SKF хотели знать, повлияет ли переход на менее дорогую конструкцию с сепаратором на срок службы подшипников. Инженеры попросили Кристера Хеллстранда, статистика, помочь в разработке эксперимента.[7]

Коробка сообщает следующее. «Результаты были оценены с помощью ускоренного испытания на долговечность ... Испытания были дорогими, потому что их нужно было проводить на реальной производственной линии, и экспериментаторы планировали провести четыре цикла со стандартной клеткой и четыре с модифицированной клеткой. Кристер спросил, есть ли есть и другие факторы, которые они хотели бы проверить. Они сказали, что есть, но добавление дополнительных прогонов превысит их бюджет. Кристер показал им, как они могут протестировать два дополнительных фактора «бесплатно» - без увеличения количества прогонов и без сокращения точность их оценки эффекта клетки. В этой схеме, называемой факторным планом 2 × 2 × 2, каждый из трех факторов будет работать на двух уровнях, включая все восемь возможных комбинаций. Различные комбинации могут быть удобно показаны как вершины куба ... "" В каждом случае стандартное состояние обозначается знаком минус, а измененное - знаком плюс. Изменившимися факторами были термообработка, соприкосновение внешнего кольца и конструкция клетки. Цифры показывают относительный срок службы подшипников. Если вы посмотрите на [график куба], вы увидите, что выбор конструкции клетки не имеет большого значения. … Но если вы усредните пары чисел для конструкции клетки, вы получите [таблицу ниже], которая показывает, что сделали два других фактора. … Это привело к удивительному открытию, что в данном конкретном случае срок службы подшипника может быть увеличен в пять раз, если вместе увеличить два фактора (факторов), связанных с сопряжением внешнего кольца и термообработкой внутреннего кольца ».
| Оскуляция - | Оскуляция + | |
|---|---|---|
| Тепло - | 18 | 23 |
| Тепло + | 21 | 106 |
«Помня о том, что подшипники, подобные этому, изготавливались десятилетиями, сначала удивительно, что на обнаружение такого важного улучшения может потребоваться так много времени. Вероятное объяснение состоит в том, что, поскольку большинство инженеров до недавнего времени использовали только один фактор время экспериментирования, взаимодействие эффекты были упущены ".
Пример
Самый простой факторный эксперимент содержит два уровня для каждого из двух факторов. Предположим, инженер хочет изучить общую мощность, потребляемую каждым из двух разных двигателей, A и B, работающих на каждой из двух разных скоростей, 2000 или 3000 об / мин. Факторный эксперимент будет состоять из четырех экспериментальных единиц: двигатель A на 2000 об / мин, двигатель B на 2000 об / мин, двигатель A на 3000 об / мин и двигатель B на 3000 об / мин. Каждая комбинация одного уровня, выбранного из каждого фактора, присутствует один раз.
Этот эксперимент представляет собой пример двух2 (или 2 × 2) факторный эксперимент, названный так потому, что он рассматривает два уровня (основание) для каждого из двух факторов (степень или верхний индекс) или #levels#factors, производя 22= 4 факториальных точки.

Дизайн может включать множество независимых переменных. В качестве еще одного примера, влияние трех входных переменных можно оценить в восьми экспериментальных условиях, показанных в виде углов куба.
Это может выполняться с репликацией или без нее, в зависимости от ее предполагаемого назначения и доступных ресурсов. Он предоставит влияние трех независимых переменных на зависимую переменную и возможные взаимодействия.
Обозначение
| А | B | |
|---|---|---|
| (1) | − | − |
| а | + | − |
| б | − | + |
| ab | + | + |
Обозначения, используемые для обозначения факторных экспериментов, передают много информации. Когда дизайн обозначен как 23 факториал - определяет количество факторов (3); сколько уровней имеет каждый фактор (2); и сколько экспериментальных условий предусмотрено в схеме (23 = 8). Аналогично 25 дизайн имеет пять факторов, каждый с двумя уровнями, и 25 = 32 экспериментальных условия. Факторные эксперименты могут включать факторы с разным количеством уровней. А 243 имеет пять факторов, четыре с двумя уровнями и один с тремя уровнями, и имеет 16 × 3 = 48 экспериментальных условий.[8]
Для экономии места точки в двухуровневом факторном эксперименте часто сокращаются строками знаков плюс и минус. Строки содержат столько символов, сколько факторов, и их значения определяют уровень каждого фактора: обычно для первого (или нижнего) уровня, и для второго (или высокого) уровня. Таким образом, точки в этом эксперименте можно представить как , , , и .
Факториальные точки также могут быть сокращены до (1), a, b и ab, где наличие буквы указывает, что указанный фактор находится на своем высоком (или втором) уровне, а отсутствие буквы указывает, что указанный фактор находится на низком (или первом) уровне (например, «а» указывает, что фактор A находится на высоком уровне, а все другие факторы имеют низкое (или первое) значение). (1) используется, чтобы указать, что все факторы имеют самые низкие (или первые) значения.
Выполнение
Для более чем двух факторов 2k Факторный эксперимент обычно можно рекурсивно спланировать из 2k−1 факторный эксперимент путем воспроизведения 2k−1 поэкспериментируйте, назначив первую реплику первому (или низкому) уровню нового фактора, а вторую реплику - второму (или высокому) уровню. Эту схему можно обобщить на: например, проектируя три реплики для трехуровневых факторов, так далее.
Факторный эксперимент позволяет оценить экспериментальная ошибка двумя способами. Эксперимент может быть воспроизведен, или принцип разреженности эффектов часто можно эксплуатировать. Репликация чаще используется для небольших экспериментов и является очень надежным способом оценки экспериментальной ошибки. Когда количество факторов велико (обычно более 5 факторов, но это зависит от приложения), копирование проекта может стать трудным в эксплуатации. В этих случаях обычно запускают только одну копию проекта и предполагают, что взаимодействия факторов более чем определенного порядка (скажем, между тремя или более факторами) пренебрежимо малы. При таком предположении оценки взаимодействий такого высокого порядка являются оценками точного нуля, а значит, действительно оценкой экспериментальной ошибки.
Когда есть много факторов, потребуется множество экспериментов, даже без повторения. Например, экспериментирование с 10 факторами на двух уровнях на каждом дает 210= 1024 комбинации. В какой-то момент это становится невозможным из-за высокой стоимости или недостатка ресурсов. В этом случае, дробные факторные планы может быть использовано.
Как и в любом статистическом эксперименте, экспериментальные серии в факторном эксперименте должны быть рандомизированы, чтобы уменьшить влияние, которое предвзятость мог иметь на результаты экспериментов. На практике это может быть большой эксплуатационной проблемой.
Факторные эксперименты можно использовать, когда существует более двух уровней каждого фактора. Однако количество экспериментальных прогонов, необходимых для трехуровневых (или более) факторных планов, будет значительно больше, чем для их двухуровневых аналогов. Следовательно, факторные планы менее привлекательны, если исследователь желает рассмотреть более двух уровней.
Анализ
Факторный эксперимент можно проанализировать с помощью ANOVA или же регрессивный анализ.[9] Чтобы вычислить основной эффект фактора «А», вычтите средний отклик всех экспериментальных запусков, для которых А был на своем низком (или первом) уровне, из среднего отклика всех экспериментальных запусков, для которых А был на своем высоком (или втором) уровне. ) уровень.
Другие полезные инструменты исследовательского анализа для факторных экспериментов включают: основные эффекты участки, графики взаимодействия, Графики Парето, а график нормальной вероятности предполагаемых эффектов.
Когда факторы непрерывны, двухуровневые факторные планы предполагают, что эффекты линейный. Если квадратичный эффект ожидается для фактора, следует использовать более сложный эксперимент, такой как центральная композитная конструкция. Оптимизация факторов, которые могут иметь квадратичный эффект, является основной целью методология поверхности отклика.
Пример анализа
Монтгомери [4] приводит следующий пример анализа факторного эксперимента :.
Инженер хотел бы увеличить скорость фильтрации (производительность) процесса для производства химического вещества и уменьшить количество формальдегида, используемого в процессе. Предыдущие попытки снизить содержание формальдегида снизили скорость фильтрации. Текущая скорость фильтрации составляет 75 галлонов в час. Учитываются четыре фактора: температура (A), давление (B), концентрация формальдегида (C) и скорость перемешивания (D). Каждый из четырех факторов будет проверяться на двух уровнях.
Далее знаки «минус» (-) и «плюс» (+) будут указывать, на каком уровне работает фактор, на низком или высоком уровне соответственно.
| А | B | C | D | Скорость фильтрации |
|---|---|---|---|---|
| − | − | − | − | 45 |
| + | − | − | − | 71 |
| − | + | − | − | 48 |
| + | + | − | − | 65 |
| − | − | + | − | 68 |
| + | − | + | − | 60 |
| − | + | + | − | 80 |
| + | + | + | − | 65 |
| − | − | − | + | 43 |
| + | − | − | + | 100 |
| − | + | − | + | 45 |
| + | + | − | + | 104 |
| − | − | + | + | 75 |
| + | − | + | + | 86 |
| − | + | + | + | 70 |
| + | + | + | + | 96 |

График основных эффектов, показывающий скорости фильтрации для низких (-) и высоких (+) настроек для каждого фактора.
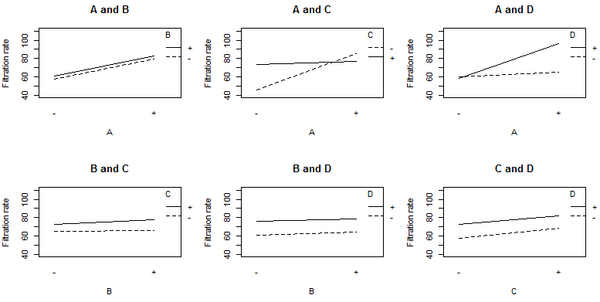
График эффектов взаимодействия, показывающий среднюю скорость фильтрации для каждой из четырех возможных комбинаций уровней для данной пары факторов.
Непараллельные линии на графике взаимодействия A: C показывают, что влияние фактора A зависит от уровня фактора C. Аналогичные результаты справедливы для взаимодействия A: D. Графики показывают, что фактор B мало влияет на скорость фильтрации. В дисперсионный анализ (ANOVA) включая все 4 фактора и все возможные условия взаимодействия между ними, получаем оценки коэффициентов, показанные в таблице ниже.
| Коэффициенты | Оценивать |
|---|---|
| Перехватить | 70.063 |
| А | 10.813 |
| B | 1.563 |
| C | 4.938 |
| D | 7.313 |
| А: Б | 0.063 |
| А: С | −9.063 |
| ДО Н.Э | 1.188 |
| ОБЪЯВЛЕНИЕ | 8.313 |
| B: D | −0.188 |
| CD | −0.563 |
| А: В: С | 0.938 |
| А: Б: Д | 2.063 |
| А: С: D | −0.813 |
| А: В: Д | −1.313 |
| А: Б: В: Д | 0.688 |
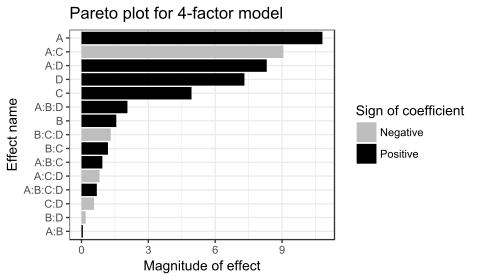
Поскольку имеется 16 наблюдений и 16 коэффициентов (пересечение, основные эффекты и взаимодействия), p-значения не могут быть рассчитаны для этой модели. Значения коэффициентов и графики показывают, что важными факторами являются A, C и D, а также условия взаимодействия A: C и A: D.
Все коэффициенты для A, C и D в ANOVA положительны, что предполагает запуск процесса со всеми тремя переменными, установленными на высокое значение. Однако основным эффектом каждой переменной является среднее значение по уровням других переменных. График взаимодействия A: C выше показывает, что влияние фактора A зависит от уровня фактора C, и наоборот. Фактор A (температура) очень мало влияет на скорость фильтрации, когда фактор C находится на уровне +. Но фактор A имеет большое влияние на скорость фильтрации, когда фактор C (формальдегид) находится на уровне -. Комбинация A на уровне + и C на уровне - дает наивысшую скорость фильтрации. Это наблюдение показывает, как однофакторный анализ может упустить важные взаимодействия. Только изменяя оба фактора A и C одновременно, инженер мог обнаружить, что эффект фактора A зависит от уровня фактора C.

Наилучшая скорость фильтрации наблюдается, когда A и D находятся на высоком уровне, а C - на низком уровне. Этот результат также соответствует цели по снижению содержания формальдегида (фактор C). Поскольку B не кажется важным, его можно исключить из модели. Выполнение ANOVA с использованием факторов A, C и D и условий взаимодействия A: C и A: D дает результат, показанный в следующей таблице, в которой все условия значимы (p-значение <0,05).
| Коэффициент | Оценивать | Стандартная ошибка | значение t | p-значение |
|---|---|---|---|---|
| Перехватить | 70.062 | 1.104 | 63.444 | 2.3 × 10−14 |
| А | 10.812 | 1.104 | 9.791 | 1.9 × 10−6 |
| C | 4.938 | 1.104 | 4.471 | 1.2 × 10−3 |
| D | 7.313 | 1.104 | 6.622 | 5.9 × 10−5 |
| А: С | −9.063 | 1.104 | −8.206 | 9.4 × 10−6 |
| ОБЪЯВЛЕНИЕ | 8.312 | 1.104 | 7.527 | 2 × 10−5 |
Смотрите также
- Комбинаторный дизайн
- Дизайн экспериментов
- Ортогональный массив
- План Плакетта-Бермана
- Методы Тагучи
- T-критерий Велча
Примечания
- ^ Йетс, Фрэнк; Мазер, Кеннет (1963). "Рональд Эйлмер Фишер". Биографические воспоминания членов Королевского общества. Лондон, Англия: Королевское общество. 9: 91–120. Дои:10.1098 / rsbm.1963.0006. Архивировано из оригинал (PDF) 18 февраля 2009 г.
- ^ Фишер, Рональд (1926). «Организация полевых экспериментов» (PDF). Журнал Министерства сельского хозяйства Великобритании. Лондон, Англия: Министерство сельского хозяйства и рыболовства. 33: 503–513.
- ^ «Самые ранние известные варианты использования некоторых слов математики (F)». jeff560.tripod.com.
- ^ а б Монтгомери, Дуглас К. (2013). Планирование и анализ экспериментов (8-е изд.). Хобокен, Нью-Джерси: Wiley. ISBN 978-1119320937.
- ^ Олерт, Гэри (2000). Первый курс по разработке и анализу экспериментов (Пересмотренная ред.). Нью-Йорк: В. Х. Фриман и компания. ISBN 978-0716735106.
- ^ Джордж Е.П., Коробка (2006). Улучшение почти всего: идеи и эссе (Пересмотренная ред.). Хобокен, Нью-Джерси: Wiley. КАК В B01FKSM9VY.
- ^ Hellstrand, C .; Oosterhoorn, A.D .; Шервин, Д. Дж .; Герсон, М. (24 февраля 1989 г.). «Необходимость современного повышения качества и некоторый опыт его внедрения в производство подшипников качения [и обсуждение]». Философские труды Королевского общества. 327 (1596): 529–537. Дои:10.1098 / рста.1989.0008.
- ^ Колледж здоровья и человеческого развития Университета Пенсильвании (22 декабря 2011 г.). «Введение в факториальные экспериментальные планы».
- ^ Коэн, Дж (1968). «Множественная регрессия как общая аналитическая система данных». Психологический бюллетень. 70 (6): 426–443. CiteSeerX 10.1.1.476.6180. Дои:10,1037 / ч0026714.
Рекомендации
- Бокс, Г. Э.; Хантер, W. G .; Хантер, Дж. С. (2005). Статистика для экспериментаторов: дизайн, инновации и открытия (2-е изд.). Вайли. ISBN 978-0-471-71813-0.








