Функция выживания - Survival function
В функция выживания это функция что дает вероятность что пациент, устройство или другой интересующий объект будут выживать сверх указанного времени.[1]
Функция выживания также известна как функция выживания[2] или же функция надежности.[3]
Период, термин функция надежности распространено в инженерное дело в то время как срок функция выживания используется в более широком диапазоне приложений, включая человеческую смертность. Другое название функции выживания - дополнительная кумулятивная функция распределения.
Определение
Позволять Т быть непрерывной случайной величиной с кумулятивная функция распределения F(т) на отрезке [0, ∞). Его функция выживания или же функция надежности является:
Примеры функций выживания
На графиках ниже показаны примеры гипотетических функций выживания. Ось абсцисс - время. По оси ординат отложено количество выживших субъектов. Графики показывают вероятность того, что субъект выживет после времени t.
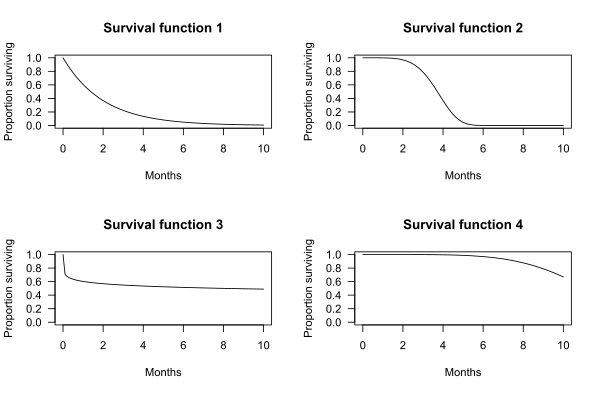
Например, для функции выживаемости 1 вероятность прожить дольше t = 2 месяцев составляет 0,37. То есть 37% испытуемых выживают более 2 месяцев.

Для функции выживаемости 2 вероятность прожить дольше t = 2 месяцев составляет 0,97. То есть 97% испытуемых выживают более 2 месяцев.

Медиана выживаемости может быть определена по функции выживаемости. Например, для функции выживаемости 2 50% субъектов выживают 3,72 месяца. Таким образом, средняя выживаемость составляет 3,72 месяца.
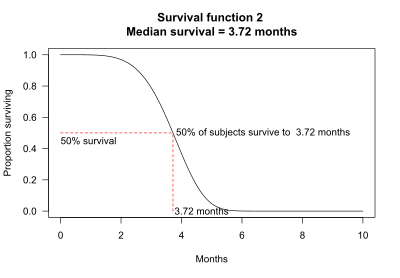
В некоторых случаях среднюю выживаемость невозможно определить по графику. Например, для функции выживаемости 4 более 50% субъектов живут дольше, чем период наблюдения в 10 месяцев.

Функция выживаемости - это один из нескольких способов описания и отображения данных о выживаемости. Еще один полезный способ отображения данных - это график, показывающий распределение времени выживания субъектов. Олькин,[4] стр. 426, дает следующий пример данных о выживаемости. Регистрировалось количество часов между последовательными отказами системы кондиционирования воздуха. Время между последовательными отказами составляет 1, 3, 5, 7, 11, 11, 11, 12, 14, 14, 14, 16, 16, 20, 21, 23, 42, 47, 52, 62, 71, 71, 87, 90, 95, 120, 120, 225, 246 и 261 час. Средняя наработка на отказ 59,6. Это среднее значение будет вскоре использовано для подгонки теоретической кривой к данным. На рисунке ниже показано распределение времени наработки на отказ. Синие галочки под графиком - это фактические часы между последовательными отказами.
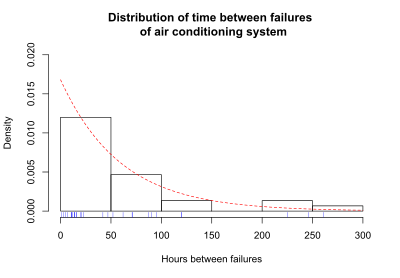
Распределение времени отказов перекрыто кривой, представляющей экспоненциальное распределение. В этом примере экспоненциальное распределение аппроксимирует распределение времени отказа. Экспоненциальная кривая представляет собой теоретическое распределение, соответствующее фактическому времени отказа. Эта конкретная экспоненциальная кривая определяется параметром лямбда, λ = 1 / (средняя наработка на отказ) = 1 / 59,6 = 0,0168. Распределение времени отказов называется функцией плотности вероятности (pdf), если время может принимать любое положительное значение. В уравнениях pdf указывается как f (t). Если время может принимать только дискретные значения (например, 1 день, 2 дня и т. Д.), Распределение времени отказа называется функция массы вероятности (pmf). Большинство методов анализа выживаемости предполагают, что время может принимать любое положительное значение, а f (t) - это pdf. Если время между наблюдаемыми отказами кондиционера приблизительно определяется с помощью экспоненциальной функции, то экспоненциальная кривая дает функцию плотности вероятности f (t) для времени отказа кондиционера.
Еще один полезный способ отображения данных о выживаемости - это график, показывающий совокупное количество отказов до каждого момента времени. Эти данные могут отображаться либо как кумулятивное количество, либо как кумулятивная доля отказов до каждого раза. На приведенном ниже графике показана совокупная вероятность (или доля) сбоев в каждый момент времени для системы кондиционирования воздуха. Линия ступеньки черного цвета показывает совокупную долю отказов. Для каждого шага внизу графика есть синяя галочка, указывающая наблюдаемое время отказа. Плавная красная линия представляет собой экспоненциальную кривую, соответствующую наблюдаемым данным.
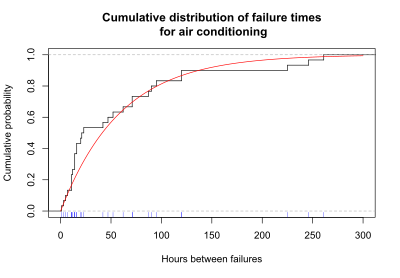
График совокупной вероятности отказов до каждого момента времени называется кумулятивная функция распределения, или CDF. В анализе выживаемости кумулятивная функция распределения дает вероятность того, что время выживания меньше или равно определенному времени t.
Пусть T - время выживания, которое является любым положительным числом. Конкретное время обозначается строчной буквой t. Кумулятивная функция распределения Т это функция
где правая часть представляет собой вероятность что случайная величина Т меньше или равно т. Если время может принимать любое положительное значение, тогда кумулятивная функция распределения F (t) является интегралом от функции плотности вероятности f (t).
Для примера кондиционирования воздуха график CDF ниже показывает, что вероятность того, что время наработки на отказ меньше или равно 100 часам, составляет 0,81, как оценивается с использованием экспоненциальной кривой, соответствующей данным.

Альтернатива графическому графику вероятности того, что время отказа меньше чем или равным 100 часам, составляет график вероятности того, что время отказа больше чем 100 часов. Вероятность того, что время отказа превышает 100 часов, должна составлять 1 минус вероятность того, что время отказа меньше или равно 100 часам, потому что общая вероятность должна быть равна 1.
Это дает
P (время отказа> 100 часов) = 1 - P (время отказа <100 часов) = 1 - 0,81 = 0,19.
Эта связь распространяется на все времена отказа:
P (T> t) = 1 - P (T Эта взаимосвязь показана на графиках ниже. График слева - это кумулятивная функция распределения, которая равна P (T В некоторых случаях, например, в примере с кондиционером, распределение продолжительности жизни может быть хорошо аппроксимировано такой функцией, как экспоненциальное распределение. В анализе выживаемости обычно используются несколько распределений, в том числе экспоненциальное, Вейбулла, гамма, нормальное, логарифмически нормальное и логарифмическое.[3][5] Эти распределения определяются параметрами. Например, нормальное (гауссово) распределение определяется двумя параметрами: средним значением и стандартным отклонением. Функции выживания, определяемые параметрами, называются параметрическими. На четырех графиках функции выживания, показанных выше, форма функции выживания определяется конкретным распределением вероятностей: функция выживания 1 определяется экспоненциальным распределением, 2 определяется распределением Вейбулла, 3 определяется лог-логистическим распределением. , а 4 определяется другим распределением Вейбулла. Для экспоненциального распределения выживаемости вероятность отказа одинакова в каждом временном интервале, независимо от возраста человека или устройства. Этот факт приводит к свойству "без памяти" экспоненциального распределения выживаемости: возраст испытуемого не влияет на вероятность неудачи в следующем временном интервале. Экспонента может быть хорошей моделью для срока службы системы, в которой детали заменяются по мере их выхода из строя.[6] Это также может быть полезно для моделирования выживания живых организмов за короткие промежутки времени. Вряд ли это хорошая модель полной продолжительности жизни живого организма.[7] Как Эфрон и Хасти [8](стр. 134) отмечают: «Если бы человеческие жизни были экспоненциальными, не было бы старых или молодых людей, только удачливые или неудачливые». Ключевое предположение экспоненциальной функции выживаемости состоит в том, что степень риска постоянна. В приведенном выше примере доля мужчин, умирающих каждый год, была постоянной и составляла 10%, что означает, что уровень опасности был постоянным. Предположение о постоянной опасности может быть неуместным. Например, среди большинства живых организмов риск смерти выше в старости, чем в среднем возрасте, то есть степень опасности со временем увеличивается. Для некоторых заболеваний, таких как рак груди, риск рецидива ниже через 5 лет, то есть степень опасности со временем уменьшается. В Распределение Вейбулла расширяет экспоненциальное распределение, чтобы обеспечить постоянство, увеличение или уменьшение степени опасности. Существует несколько других параметрических функций выживаемости, которые могут лучше соответствовать определенному набору данных, включая нормальные, логнормальные, лог-логистические и гамма-характеристики. Выбор параметрического распределения для конкретного приложения может быть сделан с помощью графических методов или с помощью формальных тестов соответствия. Эти распределения и тесты описаны в учебниках по анализу выживаемости.[1][3] Лоулесс [9]имеет обширный охват параметрических моделей. Параметрические функции выживаемости обычно используются в производственных приложениях, отчасти потому, что они позволяют оценить функцию выживаемости за пределами периода наблюдения. Однако для надлежащего использования параметрических функций необходимо, чтобы данные были хорошо смоделированы выбранным распределением. Если подходящее распределение недоступно или не может быть определено до клинического испытания или эксперимента, тогда непараметрические функции выживаемости предлагают полезную альтернативу. Параметрическая модель выживания может оказаться невозможной или нежелательной. В этих ситуациях наиболее распространенным методом моделирования функции выживания является непараметрический метод. Оценка Каплана – Мейера. Каждая функция выживания S(т) является монотонно убывающий, т.е. для всех . Это собственность случайная переменная который отображает набор событий, обычно связанных со смертностью или отказом какой-либо системы, на время. В время, т = 0, представляет собой некое происхождение, обычно начало исследования или начало работы некоторой системы. S(0) обычно равно единице, но может быть меньше, чтобы представить вероятность что система выходит из строя сразу после работы. Поскольку CDF является непрерывный вправо функция, функция выживания также непрерывна справа.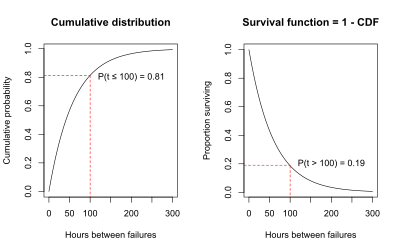
Параметрические функции выживания
Экспоненциальная функция выживания
Функция выживания Вейбулла
Другие параметрические функции выживания
Непараметрические функции выживания
Характеристики
Смотрите также
Рекомендации





