Коэнс каппа - Википедия - Cohens kappa
Коэффициент каппа Коэна (κ) это статистика что используется для измерения межэкспертная надежность (а также Внутриэкспертная надежность ) для качественных (категориальных) позиций.[1] Обычно считается, что это более надежная мера, чем простой расчет процента согласия, поскольку κ учитывает возможность случайного заключения соглашения. Вокруг каппы Коэна ведутся споры из-за сложности интерпретации индексов согласия. Некоторые исследователи предположили, что концептуально проще оценить несоответствие между элементами.[2] Увидеть Ограничения раздел для более подробной информации.
История
Первое упоминание о каппа-подобной статистике приписывается Гальтону (1892);[3] см. Smeeton (1985).[4].
Основополагающая статья, представляющая каппа как новую технику, была опубликована Джейкоб Коэн в журнале Образовательные и психологические измерения в 1960 г.[5]
Определение
Каппа Коэна измеряет согласие между двумя оценщиками, каждый из которых классифицирует N предметы в C взаимоисключающие категории. Определение является:
куда по относительное наблюдаемое согласие между оценщиками (идентично точность ), и пе - это гипотетическая вероятность случайного совпадения, использующая наблюдаемые данные для вычисления вероятностей того, что каждый наблюдатель случайно увидит каждую категорию. Если оценщики полностью согласны, то . Если между оценщиками нет согласия, кроме того, что можно было бы ожидать случайно (как указано пе), . Статистика может быть отрицательной,[6] что означает, что между двумя оценщиками нет эффективного согласия или что согласие хуже случайного.
За k категории, N наблюдения для категоризации и количество раз оценщик я предсказанная категория k:
Это выводится из следующей конструкции:
Где - это оценочная вероятность того, что и эксперт 1, и эксперт 2 классифицируют один и тот же предмет как k, в то время как - это оценочная вероятность того, что оценщик 1 классифицирует элемент как k (и аналогично для оценщика 2). основан на предположении, что рейтинг двух оценщиков независимый. Период, термин оценивается с использованием количества пунктов, классифицированных как k оценщиком 1 () деленное на общее количество элементов для классификации (): (и аналогично для оценщика 2).
Примеры
Простой пример
Предположим, вы анализировали данные, относящиеся к группе из 50 человек, подавших заявку на грант. Каждое предложение о гранте было прочитано двумя читателями, и каждый из них сказал либо «Да», либо «Нет» на предложение. Предположим, что данные подсчета разногласий были следующими, где A и B - считыватели, данные на главной диагонали матрицы (a и d) подсчитывают количество соглашений, а недиагональные данные (b и c) подсчитывают количество разногласий:
| B | |||
|---|---|---|---|
| да | Нет | ||
| А | да | а | б |
| Нет | c | d | |
например
| B | |||
|---|---|---|---|
| да | Нет | ||
| А | да | 20 | 5 |
| Нет | 10 | 15 | |
Наблюдаемое пропорциональное согласие:
Вычислять пе (вероятность случайного совпадения) отметим, что:
- Читатель А сказал «Да» 25 заявителям и «Нет» 25 заявителям. Таким образом, читатель А сказал «Да» в 50% случаев.
- Читатель Б сказал «Да» 30 заявителям и «Нет» 20 заявителям. Таким образом, читатель Б сказал «Да» в 60% случаев.
Таким образом, ожидаемая вероятность того, что оба ответят «да» наугад, равна:
По аналогии:
Общая вероятность случайного согласия - это вероятность того, что они согласились либо на Да, либо на Нет, то есть:
Итак, применив нашу формулу для Каппы Коэна, мы получим:
Те же проценты, но разные числа
Случай, который иногда считается проблемой с Каппа Коэна, возникает при сравнении каппы, рассчитанной для двух пар оценщиков, с двумя оценщиками в каждой паре, имеющими одинаковое процентное согласие, но одна пара дает одинаковое количество оценок в каждом классе, а другая пара дают разное количество оценок в каждом классе.[7] (В приведенных ниже случаях в уведомлении B в первом случае указано 70 «да» и 30 номеров, но во втором эти числа поменяны местами.) Например, в следующих двух случаях существует одинаковое согласие между A и B (60 из 100 в обоих случаях) с точки зрения согласия в каждом классе, поэтому мы ожидаем, что относительные значения Каппы Коэна отразят это. Однако вычисление Каппы Коэна для каждого:
| B | |||
|---|---|---|---|
| да | Нет | ||
| А | да | 45 | 15 |
| Нет | 25 | 15 | |
| B | |||
|---|---|---|---|
| да | Нет | ||
| А | да | 25 | 35 |
| Нет | 5 | 35 | |
мы обнаруживаем, что он показывает большее сходство между A и B во втором случае по сравнению с первым. Это связано с тем, что, хотя процентное совпадение такое же, процентное совпадение, которое могло бы возникнуть «случайно», значительно выше в первом случае (0,54 по сравнению с 0,46).
Характеристики
Проверка гипотез и доверительный интервал
P-значение для каппа редко сообщается, вероятно, потому что даже относительно низкие значения каппа, тем не менее, могут значительно отличаться от нуля, но не иметь достаточную величину, чтобы удовлетворить исследователей.[8]:66Тем не менее, стандартная ошибка описана[9]и вычисляется различными компьютерными программами.[10]
Доверительные интервалы for Kappa можно построить для ожидаемых значений Kappa, если бы у нас было проверено бесконечное количество элементов, используя следующую формулу:[1]
Где это стандартный нормальный процентиль, когда , и
Это рассчитывается путем игнорирования этого пе оценивается на основе данных, и путем обработки по как оценочная вероятность биномиальное распределение при использовании асимптотической нормальности (т. е .: при условии, что количество элементов велико и что по не близко ни к 0, ни к 1). (и CI в целом) также можно оценить с помощью бутстрап методы.
Интерпретация величины

Если статистическая значимость не является полезным ориентиром, какая величина каппа отражает адекватное согласие? Рекомендации были бы полезны, но на его величину могут влиять другие факторы, кроме согласия, что делает интерпретацию данной величины проблематичной. Как отметили Сим и Райт, двумя важными факторами являются распространенность (равновероятны ли коды или их вероятности различаются) и систематическая ошибка (предельные вероятности для двух наблюдателей похожи или разные). При прочих равных, каппа выше, когда коды равновероятны. С другой стороны, каппа выше, когда коды распределяются асимметрично двумя наблюдателями. В отличие от вариаций вероятности, влияние систематической ошибки больше, когда каппа мала, чем когда она большая.[11]:261–262
Еще один фактор - количество кодов. По мере увеличения количества кодов каппы становятся выше. Основываясь на имитационном исследовании, Бейкман и его коллеги пришли к выводу, что для склонных к ошибкам наблюдателей значения каппа были ниже, когда кодов было меньше. И, в соответствии с утверждением Sim & Wrights относительно распространенности, каппа была выше, когда коды были примерно равновероятными. Таким образом, Bakeman et al. пришел к выводу, что «ни одно значение каппы не может считаться универсально приемлемым».[12]:357 Они также предоставляют компьютерную программу, которая позволяет пользователям вычислять значения каппа, определяя количество кодов, их вероятность и точность наблюдателя. Например, с учетом равновероятных кодов и наблюдателей с точностью 85% значения каппа составляют 0,49, 0,60, 0,66 и 0,69 при количестве кодов 2, 3, 5 и 10 соответственно.
Тем не менее, рекомендации по величине появились в литературе. Пожалуй, первыми были Ландис и Кох,[13]которые охарактеризовали значения <0 как отсутствие согласия и 0–0,20 как незначительное, 0,21–0,40 как удовлетворительное, 0,41–0,60 как умеренное, 0,61–0,80 как существенное и 0,81–1 как почти полное совпадение. Однако этот набор руководящих принципов не является общепринятым; Ландис и Кох не представили никаких доказательств в поддержку этого, а основали это на личном мнении. Было отмечено, что эти рекомендации могут быть скорее вредными, чем полезными.[14] Флейса[15]:218 столь же произвольные рекомендации характеризуют каппы выше 0,75 как отличные, от 0,40 до 0,75 как от удовлетворительных до хороших и ниже 0,40 как плохие.
Каппа максимум
Каппа принимает теоретическое максимальное значение, равное 1, только когда оба наблюдателя распределяют коды одинаково, то есть когда соответствующие суммы строк и столбцов идентичны. Все, что меньше, - это не идеальное согласие. Тем не менее, максимальное значение каппа, которого может достичь при неравном распределении, помогает интерпретировать фактически полученное значение каппа. Уравнение для κ максимум:[16]
куда , как обычно, ,
k = количество кодов, - вероятности строк, и - вероятности столбца.
Ограничения
Каппа - это индекс, который учитывает наблюдаемое согласие относительно базового соглашения. Тем не менее, исследователи должны тщательно обдумать, актуально ли исходное соглашение Каппы для конкретного вопроса исследования. Базовый уровень Каппы часто описывается как случайное совпадение, что верно лишь отчасти. Базовое соглашение Kappa - это соглашение, которого можно было бы ожидать из-за случайного распределения, учитывая количества, указанные в предельных суммах квадратной таблицы непредвиденных обстоятельств. Таким образом, Каппа = 0, когда наблюдаемое распределение очевидно случайное, независимо от количественного несогласия, ограниченного предельными итогами. Однако для многих приложений исследователи должны быть больше заинтересованы в количественном несогласии в предельных итоговых суммах, чем в несогласии распределения, как описано в дополнительной информации на диагонали квадратной таблицы непредвиденных обстоятельств. Таким образом, для многих приложений базовый уровень Каппы скорее отвлекает, чем разъясняет. Рассмотрим следующий пример:
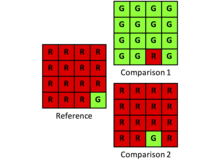
| Ссылка | |||
|---|---|---|---|
| грамм | р | ||
| Сравнение | грамм | 1 | 14 |
| р | 0 | 1 | |
Доля несогласия составляет 14/16 или 0,875. Несогласие связано с количеством, поскольку распределение является оптимальным. Каппа составляет 0,01.
| Ссылка | |||
|---|---|---|---|
| грамм | р | ||
| Сравнение | грамм | 0 | 1 |
| р | 1 | 14 | |
Доля несогласия составляет 2/16 или 0,125. Несогласие связано с распределением, потому что количества идентичны. Каппа составляет -0,07.
Здесь несогласие по количеству и распределению отчетов является информативным, в то время как Каппа скрывает информацию. Кроме того, Каппа представляет некоторые проблемы при расчетах и интерпретации, поскольку Каппа - это соотношение. Коэффициент Каппы может возвращать неопределенное значение из-за нуля в знаменателе. Более того, отношение не раскрывает ни числитель, ни знаменатель. Для исследователей более информативно сообщать о разногласиях по двум компонентам: количеству и распределению. Эти два компонента описывают взаимосвязь между категориями более четко, чем одна сводная статистика. Когда целью является точность прогнозов, исследователям легче начать думать о способах улучшения прогнозов, используя два компонента количества и распределения, а не одно отношение Каппа.[2]
Некоторые исследователи выразили обеспокоенность по поводу тенденции κ принимать частоты наблюдаемых категорий как данность, что может сделать его ненадежным для измерения согласия в таких ситуациях, как диагностика редких заболеваний. В этих ситуациях κ имеет тенденцию недооценивать согласие по редкой категории.[17] По этой причине κ считается чрезмерно консервативной мерой согласия.[18] Другие[19][нужна цитата ] оспаривать утверждение, что каппа «учитывает» случайное соглашение. Чтобы сделать это эффективно, потребуется явная модель того, как шанс влияет на решения оценщика. Так называемая случайная корректировка статистики каппа предполагает, что, когда она не полностью уверена, оценщики просто предполагают - очень нереалистичный сценарий.
Связанная статистика
Пи Скотта
Аналогичная статистика, называемая число Пи, был предложен Скоттом (1955). Каппа Коэна и Пи Скотта отличаются тем, как пе рассчитывается.
Каппа Флейса
Обратите внимание, что каппа Коэна измеряет согласие между два только оценщики. Для аналогичной степени согласия (Каппа Флейса ) используется при наличии более двух оценщиков, см. Fleiss (1971). Каппа Флейсса, однако, представляет собой многократное обобщение Пи Скотта статистика, а не каппа Коэна. Каппа также используется для сравнения производительности в машинное обучение, но направленная версия, известная как Информированность или же Статистика Юдена J считается более подходящим для обучения с учителем.[20]
Взвешенная каппа
Взвешенная каппа позволяет оценивать разногласия по-разному.[21] и это особенно полезно при заказе кодов.[8]:66 Используются три матрицы: матрица наблюдаемых баллов, матрица ожидаемых баллов, основанных на случайном согласовании, и матрица весов. Ячейки матрицы весов, расположенные по диагонали (от верхнего левого угла до нижнего правого), представляют собой согласование и, следовательно, содержат нули. Недиагональные ячейки содержат веса, указывающие на серьезность несогласия. Часто ячейки, расположенные на одной диагонали, имеют вес 1, две - на 2 и т. Д.
Уравнение для взвешенного κ:
куда k= количество кодов и , , и - элементы в матрице весов, наблюдаемой и ожидаемой соответственно. Когда диагональные ячейки содержат веса 0, а веса всех недиагональных ячеек 1, эта формула дает то же значение каппа, что и расчет, приведенный выше.
Смотрите также
Рекомендации
- ^ а б МакХью, Мэри Л. (2012). «Межэкспертная надежность: статистика каппа». Биохимия Медика. 22 (3): 276–282. Дои:10.11613 / bm.2012.031. ЧВК 3900052. PMID 23092060.
- ^ а б Понтий, Роберт; Миллонес, Марко (2011). «Смерть Каппе: возникновение разногласий по количеству и разногласий по распределению для оценки точности». Международный журнал дистанционного зондирования. 32 (15): 4407–4429. Bibcode:2011IJRS ... 32.4407P. Дои:10.1080/01431161.2011.552923. S2CID 62883674.
- ^ Гальтон, Ф. (1892) Отпечатки пальцев Макмиллан, Лондон.
- ^ Смитон, Северная Каролина (1985). «Ранняя история статистики Каппа». Биометрия. 41 (3): 795. JSTOR 2531300.
- ^ Коэн, Джейкоб (1960). «Коэффициент согласованности номинальных шкал». Образовательные и психологические измерения. 20 (1): 37–46. Дои:10.1177/001316446002000104. HDL:1942/28116. S2CID 15926286.
- ^ Сим, Юлий; Райт, Крис С. (2005). «Статистика Каппа в исследованиях надежности: требования к использованию, интерпретации и размеру выборки». Физиотерапия. 85 (3): 257–268. Дои:10.1093 / ptj / 85.3.257. ISSN 1538-6724. PMID 15733050.
- ^ Килем Гвет (май 2002 г.). «Надежность между оценщиками: зависимость от распространенности черт и предельной однородности» (PDF). Статистические методы оценки надежности различных оценщиков. 2: 1–10. Архивировано из оригинал (PDF) на 2011-07-07. Получено 2011-02-02.
- ^ а б Bakeman, R .; Готтман, Дж. М. (1997). Наблюдение за взаимодействием: введение в последовательный анализ (2-е изд.). Кембридж, Великобритания: Издательство Кембриджского университета. ISBN 978-0-521-27593-4.
- ^ Fleiss, J.L .; Cohen, J .; Эверитт, Б.С. (1969). «Большая выборка стандартных ошибок каппа и взвешенной каппы». Психологический бюллетень. 72 (5): 323–327. Дои:10,1037 / ч0028106.
- ^ Робинсон, Б.Ф .; Бакеман Р. (1998). «ComKappa: программа для Windows 95 для расчета каппа и связанной статистики». Методы, инструменты и компьютеры исследования поведения. 30 (4): 731–732. Дои:10.3758 / BF03209495.
- ^ Сим, Дж; Райт, C.C (2005). «Статистика Каппа в исследованиях надежности: требования к использованию, интерпретации и размеру выборки». Физиотерапия. 85 (3): 257–268. Дои:10.1093 / ptj / 85.3.257. PMID 15733050.
- ^ Bakeman, R .; Quera, V .; McArthur, D .; Робинсон, Б.Ф. (1997). «Обнаружение последовательных моделей и определение их надежности с помощью ошибочных наблюдателей». Психологические методы. 2 (4): 357–370. Дои:10.1037 / 1082-989X.2.4.357.
- ^ Landis, J.R .; Кох, Г. (1977). «Измерение согласия наблюдателя для категориальных данных». Биометрия. 33 (1): 159–174. Дои:10.2307/2529310. JSTOR 2529310. PMID 843571.
- ^ Гвет, К. (2010). "Справочник по надежности между оценщиками (второе издание) " ISBN 978-0-9708062-2-2[страница нужна ]
- ^ Флейсс, Дж. Л. (1981). Статистические методы расчета ставок и пропорций (2-е изд.). Нью-Йорк: Джон Вили. ISBN 978-0-471-26370-8.
- ^ Umesh, U. N .; Peterson, R.A .; Заубер М. Х. (1989). «Межсудейское соглашение и максимальное значение каппы». Образовательные и психологические измерения. 49 (4): 835–850. Дои:10.1177/001316448904900407. S2CID 123306239.
- ^ Виера, Энтони Дж .; Гаррет, Джоан М. (2005). «Понимание соглашения между наблюдателями: статистика каппа». Семейная медицина. 37 (5): 360–363. PMID 15883903.
- ^ Strijbos, J .; Martens, R .; Prins, F .; Йохемс, В. (2006). «Контент-анализ: о чем они говорят?». Компьютеры и образование. 46: 29–48. CiteSeerX 10.1.1.397.5780. Дои:10.1016 / j.compedu.2005.04.002.
- ^ Uebersax, JS. (1987). «Разнообразие моделей принятия решений и измерение согласия между экспертами» (PDF). Психологический бюллетень. 101: 140–146. CiteSeerX 10.1.1.498.4965. Дои:10.1037/0033-2909.101.1.140. Архивировано из оригинал (PDF) на 2016-03-03. Получено 2010-10-16.
- ^ Пауэрс, Дэвид М. В. (2012). «Проблема с каппой» (PDF). Конференция Европейского отделения Ассоциации компьютерной лингвистики (EACL2012) Совместный семинар ROBUS-UNSUP. Архивировано из оригинал (PDF) на 2016-05-18. Получено 2012-07-20.
- ^ Коэн, Дж. (1968). «Взвешенная каппа: Соглашение о номинальной шкале с резервом на масштабное несогласие или частичное зачисление». Психологический бюллетень. 70 (4): 213–220. Дои:10,1037 / ч0026256. PMID 19673146.
дальнейшее чтение
- Banerjee, M .; Капоццоли, Мишель; Максуини, Лаура; Синха, Дебаджьоти (1999). "Beyond Kappa: Обзор мер соглашения между экспертами". Канадский статистический журнал. 27 (1): 3–23. Дои:10.2307/3315487. JSTOR 3315487.
- Brennan, R.L .; Предигер, Д. Дж. (1981). «Коэффициент λ: некоторые виды использования, неправильное использование и альтернативы». Образовательные и психологические измерения. 41 (3): 687–699. Дои:10.1177/001316448104100307. S2CID 122806628.
- Коэн, Джейкоб (1960). «Коэффициент согласования номинальных шкал». Образовательные и психологические измерения. 20 (1): 37–46. Дои:10.1177/001316446002000104. HDL:1942/28116. S2CID 15926286.
- Коэн, Дж. (1968). «Взвешенная каппа: Соглашение по номинальной шкале с резервом на масштабное несогласие или частичное зачисление». Психологический бюллетень. 70 (4): 213–220. Дои:10,1037 / ч0026256. PMID 19673146.
- Флейсс, Дж. Л. (1971). «Измерение номинальной шкалы согласия между многими оценщиками». Психологический бюллетень. 76 (5): 378–382. Дои:10,1037 / ч0031619.
- Флейсс, Дж. Л. (1981) Статистические методы расчета ставок и пропорций. 2-е изд. (Нью-Йорк: Джон Уайли) стр. 38–46.
- Fleiss, J.L .; Коэн, Дж. (1973). «Эквивалентность взвешенного каппа и коэффициента внутриклассовой корреляции как меры надежности». Образовательные и психологические измерения. 33 (3): 613–619. Дои:10.1177/001316447303300309. S2CID 145183399.
- Гвет, Килем Л. (2014) Справочник по надежности между оценщиками, четвертое издание, (Гейтерсбург: Advanced Analytics, LLC) ISBN 978-0970806284
- Гвет, К. (2008). «Вычисление межэкспертной надежности и ее дисперсии при наличии высокого согласия» (PDF). Британский журнал математической и статистической психологии. 61 (Пт 1): 29–48. Дои:10.1348 / 000711006X126600. PMID 18482474. Архивировано из оригинал (PDF) на 2016-03-03. Получено 2010-06-16.
- Гвет, К. (2008). «Оценка дисперсии надежности разных оценщиков номинальной шкалы со случайным отбором оценщиков» (PDF). Психометрика. 73 (3): 407–430. Дои:10.1007 / s11336-007-9054-8. S2CID 20827973.
- Гвет, К. (2008). "Надежность внутри системы." Энциклопедия клинических испытаний Wiley, Copyright 2008 John Wiley & Sons, Inc.
- Скотт, В. (1955). «Надежность контент-анализа: пример кодирования номинальной шкалы». Общественное мнение Ежеквартально. 17 (3): 321–325. Дои:10.1086/266577.
- Sim, J .; Райт, К. С. (2005). «Статистика Каппа в исследованиях надежности: требования к использованию, интерпретации и размеру выборки». Физиотерапия. 85 (3): 257–268. Дои:10.1093 / ptj / 85.3.257. PMID 15733050.
- Уорренс, Дж. (2011). «Каппа Коэна - это средневзвешенное значение». Статистическая методология. 8 (6): 473–484. Дои:10.1016 / j.stamet.2011.06.002.
внешняя ссылка
- Каппа, ее значение, проблемы и несколько альтернатив
- Kappa Statistics: плюсы и минусы
- Программные реализации


































