Иметь в виду - Mean

Есть несколько видов иметь в виду в математика, особенно в статистика.

Для набор данных, то среднее арифметическое, также называемый ожидаемое значение или же средний, является центральным значением дискретного набора чисел: в частности, сумма значений, деленная на количество значений. Среднее арифметическое набора чисел Икс₁, Икс₂, ..., Икс_п обычно обозначается ${ displaystyle { bar {x}}}$^{[примечание 1]}. Если бы набор данных был основан на серии наблюдений, полученных отбор проб из статистическая совокупность, среднее арифметическое - это выборочное среднее (обозначено ${ displaystyle { bar {x}}}$), чтобы отличить его от среднего значения основного распределения, Средняя численность населения (обозначено ${ displaystyle mu}$ или же ${ displaystyle mu _ {x}}$^{[заметка 2]}).^[1][2]

В вероятность и статистика, то Средняя численность населения, или ожидаемое значение, является мерой основная тенденция любой из распределение вероятностей или из случайная переменная характеризуется этим распределением.^[3] В дискретное распределение вероятностей случайной величины Икс, среднее значение равно сумме всех возможных значений, взвешенных по вероятности этого значения; то есть вычисляется путем взятия произведения каждого возможного значения Икс из Икс и его вероятность п(Икс), а затем сложив все эти продукты вместе, получив ${ displaystyle mu = sum xp (x) ....}$.^[4][5] Аналогичная формула применима к случаю непрерывное распределение вероятностей. Не каждое распределение вероятностей имеет определенное среднее значение (см. Распределение Коши для примера). Более того, для некоторых распределений среднее значение может быть бесконечным.

Для конечной совокупности Средняя численность населения стоимости имущества равна среднему арифметическому данной собственности с учетом каждого члена населения. Например, средний рост популяции равен сумме роста каждой особи, деленной на общее количество особей. Среднее значение выборки может отличаться от среднего значения генеральной совокупности, особенно для небольших выборок. В закон больших чисел утверждает, что чем больше размер выборки, тем больше вероятность того, что среднее по выборке будет близко к среднему по генеральной совокупности.^[6]

Помимо вероятности и статистики, в исследованиях часто используется широкий спектр других понятий среднего значения. геометрия и математический анализ; примеры приведены ниже.

Виды средств

Пифагорейские средние

Среднее арифметическое (AM)

В среднее арифметическое (или просто иметь в виду) списка чисел - это сумма всех чисел, деленная на количество чисел. Аналогично, среднее значение выборки ${ displaystyle x_ {1}, x_ {2}, ldots, x_ {n}}$, обычно обозначаемый ${ displaystyle { bar {x}}}$,^[1] представляет собой сумму значений выборки, деленную на количество элементов в выборке.

${ displaystyle { bar {x}} = { frac {1} {n}} left ( sum _ {i = 1} ^ {n} {x_ {i}} right) = { frac { x_ {1} + x_ {2} + cdots + x_ {n}} {n}}}$

Например, среднее арифметическое пяти значений: 4, 36, 45, 50, 75 равно:

${ displaystyle { frac {4 + 36 + 45 + 50 + 75} {5}} = { frac {210} {5}} = 42.}$

Среднее геометрическое (GM)

В среднее геометрическое - это среднее значение, которое полезно для наборов положительных чисел, которые интерпретируются в соответствии с их произведением (как в случае с темпами роста), а не их суммой (как в случае со средним арифметическим):

${ displaystyle { bar {x}} = left ( prod _ {i = 1} ^ {n} {x_ {i}} right) ^ { frac {1} {n}} = left ( x_ {1} x_ {2} cdots x_ {n} right) ^ { frac {1} {n}}}$ ^[7]

Например, среднее геометрическое пяти значений: 4, 36, 45, 50, 75 составляет:

${ displaystyle (4 times 36 times 45 times 50 times 75) ^ { frac {1} {5}} = { sqrt [{5}] {24 ; 300 ; 000}} = 30 .}$

Среднее гармоническое (HM)

В гармоническое среднее - среднее значение, которое полезно для наборов чисел, которые определены относительно некоторых единица измерения, как и в случае скорость (т.е. расстояние в единицу времени):

${ displaystyle { bar {x}} = n left ( sum _ {i = 1} ^ {n} { frac {1} {x_ {i}}} right) ^ {- 1}}$

Например, гармоническое среднее пяти значений: 4, 36, 45, 50, 75 равно

${ displaystyle { frac {5} {{ tfrac {1} {4}} + { tfrac {1} {36}} + { tfrac {1} {45}} + { tfrac {1} { 50}} + { tfrac {1} {75}}}} = { frac {5} {; { tfrac {1} {3}} ;}} = 15.}$

Отношения между AM, GM и HM

Доказательство без слов из неравенство средних арифметических и геометрических:
PR - диаметр круга с центром в точке O; его радиус AO равен среднее арифметическое из а и б. С использованием теорема о среднем геометрическом, треугольник PGR высота GQ - это среднее геометрическое. Для любого соотношения а:б, АО ≥ GQ.

AM, GM и HM удовлетворяют этим неравенствам:

${ Displaystyle mathrm {AM} geq mathrm {GM} geq mathrm {HM} ,}$

Равенство имеет место тогда и только тогда, когда все элементы данной выборки равны.

Статистическое местоположение

это Сравнение среднего арифметического, медиана и Режим из двух перекошенных (лог-нормальный ) раздачи.

Геометрическая визуализация режима, медианы и среднего значения произвольной функции плотности вероятности.^[8]

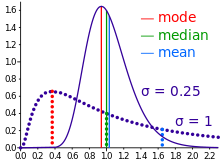
В описательная статистика среднее значение можно спутать с медиана, Режим или же средний диапазон, поскольку любой из них можно назвать "средним" (более формально, мера основная тенденция ). Среднее значение набора наблюдений - это среднее арифметическое значений; однако для перекошенные распределения, среднее значение не обязательно совпадает со средним значением (медиана) или наиболее вероятным значением (режим). Например, средний доход обычно искажается вверх небольшим количеством людей с очень большими доходами, так что большинство из них имеет доход ниже среднего. Напротив, средний доход - это уровень, на котором половина населения находится ниже, а половина - выше. Режим дохода является наиболее вероятным доходом и благоприятствует большему количеству людей с более низкими доходами. Хотя медиана и мода часто являются более интуитивными мерами для таких искаженных данных, многие искаженные распределения на самом деле лучше всего описываются их средним значением, включая экспоненциальный и Пуассон раздачи.

Среднее значение распределения вероятностей

Среднее значение распределение вероятностей является долгосрочным средним арифметическим значением случайная переменная имея это распределение. Если случайная величина обозначена как ${ displaystyle X}$, то он также известен как ожидаемое значение из ${ displaystyle X}$ (обозначено ${ Displaystyle E (X)}$).^[1] Для дискретное распределение вероятностей, среднее значение равно ${ displaystyle textstyle sum xP (x)}$, где сумма берется по всем возможным значениям случайной величины и ${ Displaystyle P (x)}$ это функция массы вероятности. Для непрерывное распространение, среднее значение ${ displaystyle textstyle int _ {- infty} ^ { infty} xf (x) , dx}$, куда ${ displaystyle f (x)}$ это функция плотности вероятности.^[5] Во всех случаях, включая те, в которых распределение не является ни дискретным, ни непрерывным, среднее значение - это Интеграл Лебега случайной величины относительно ее вероятностная мера. Среднее значение не обязательно должно существовать или быть конечным; для некоторых вероятностных распределений среднее значение бесконечно (+∞ или же −∞), в то время как для других среднее значение неопределенный.

Обобщенные средства

Средняя мощность

В обобщенное среднее, также известное как среднее значение мощности или среднее Гельдера, представляет собой абстракцию квадратичных, арифметических, геометрических и гармонических средних. Он определен для набора п положительные числа Икс_я к

${ displaystyle { bar {x}} (m) = left ({ frac {1} {n}} sum _ {i = 1} ^ {n} x_ {i} ^ {m} right) ^ { frac {1} {m}}}$ ^[7]

Выбирая разные значения параметра м, получаются следующие виды средств:

${ Displaystyle м rightarrow infty}$	максимум из ${ displaystyle x_ {i}}$
${ displaystyle m = 2}$	среднее квадратичное
${ displaystyle m = 1}$	среднее арифметическое
${ displaystyle m rightarrow 0}$	среднее геометрическое
${ displaystyle m = -1}$	гармоническое среднее
${ displaystyle m rightarrow - infty}$	минимум из ${ displaystyle x_ {i}}$

ж-иметь в виду

Это можно обобщить далее как обобщенный ж-иметь в виду

${ displaystyle { bar {x}} = f ^ {- 1} left ({{ frac {1} {n}} sum _ {i = 1} ^ {n} {f left (x_ { i} right)}} right)}$

и снова подходящий выбор обратимого ж дам

${ Displaystyle е (х) = х}$	среднее арифметическое,
${ displaystyle f (x) = { frac {1} {x}}}$	гармоническое среднее,
${ Displaystyle е (х) = х ^ {м}}$	среднее значение мощности,
${ Displaystyle е (х) = пер (х)}$	среднее геометрическое.

Иногда набор чисел может содержать выбросы (т.е. значения данных, которые намного ниже или намного выше, чем другие). Часто выбросы - это ошибочные данные, вызванные артефакты. В этом случае можно использовать усеченное среднее. Он включает в себя отбрасывание заданных частей данных на верхнем или нижнем конце, обычно равное количество на каждом конце, а затем взятие среднего арифметического оставшихся данных. Количество удаленных значений указывается в процентах от общего количества значений.

Среднее арифметическое взвешенное

В взвешенное среднее арифметическое (или средневзвешенное значение) используется, если нужно объединить средние значения из выборок одной и той же совокупности с разными размерами выборок:

${ displaystyle { bar {x}} = { frac { sum _ {i = 1} ^ {n} {w_ {i} x_ {i}}} { sum _ {i = 1} ^ {n } w_ {i}}}.}$ ^[7]

Веса ${ displaystyle w_ {i}}$ представляют размеры различных образцов. В других приложениях они представляют собой меру надежности влияния соответствующих значений на среднее значение.

Усеченное среднее

Иногда набор чисел может содержать выбросы (т.е. значения данных, которые намного ниже или намного выше, чем другие). Часто выбросы - это ошибочные данные, вызванные артефакты. В этом случае можно использовать усеченное среднее. Он включает в себя отбрасывание заданных частей данных на верхнем или нижнем конце, обычно равное количество на каждом конце, а затем взятие среднего арифметического оставшихся данных. Количество удаленных значений указывается в процентах от общего количества значений.

Межквартильное среднее

В межквартильное среднее является конкретным примером усеченного среднего. Это просто среднее арифметическое после удаления самой низкой и самой высокой четвертей значений.

${ displaystyle { bar {x}} = { frac {2} {n}} ; sum _ {i = { frac {n} {4}} + 1} ^ {{ frac {3} {4}} п} ! ! X_ {i}}$

при условии, что значения упорядочены, это просто конкретный пример взвешенного среднего для определенного набора весов.

Среднее значение функции

В некоторых случаях математики могут вычислить среднее бесконечное (или даже бесчисленный ) набор значений. Это может произойти при расчете среднего значения ${ Displaystyle у _ { текст {аве}}}$ функции ${ displaystyle f (x)}$. Интуитивно, среднее значение функции можно представить как вычисление площади под участком кривой с последующим делением на длину этого участка. Это можно сделать грубо, считая квадраты на миллиметровой бумаге, а точнее говоря, интеграция. Формула интегрирования записывается как:

${ displaystyle y _ { text {ave}} (a, b) = { frac {1} {b-a}} int limits _ {a} ^ {b} ! f (x) , dx}$

В этом случае необходимо следить за тем, чтобы интеграл сходился. Но среднее значение может быть конечным, даже если сама функция в некоторых точках стремится к бесконечности.

Среднее значение углов и циклических величин

Углы, время суток и другие циклические величины требуют модульная арифметика складывать и иначе комбинировать числа. Во всех этих ситуациях не будет единственного средства. Например, время за час до и после полуночи равноудалено как полуночи, так и полудню. Также возможно, что никакого среднего не существует. Рассмотрим цветовой круг - нет никакого набора всех цветов. В таких ситуациях вы должны решить, какое среднее значение будет наиболее полезным. Вы можете сделать это, настроив значения перед усреднением, или используя специализированный подход к среднему круговому количеству.

Фреше означает

В Фреше означает дает способ определения «центра» распределения массы на поверхность или, в более общем смысле, Риманово многообразие. В отличие от многих других средств, среднее значение Фреше определяется в пространстве, элементы которого не обязательно складываются или умножаются на скаляры. Керхер означает (назван в честь Германа Керхера).

Другие средства

Распределение выборочного среднего

Среднее арифметическое значение численность населения, или среднее значение населения, часто обозначают μ.^[1] Среднее значение выборки ${ displaystyle { bar {x}}}$ (среднее арифметическое значений выборки, взятой из генеральной совокупности) оценщик среднего генерального значения, поскольку его ожидаемое значение равно среднему значению генеральной совокупности (т. е. объективный оценщик ). Среднее значение выборки случайная переменная, а не константа, так как его вычисленное значение будет случайным образом различаться в зависимости от того, какие члены совокупности отбираются, и, следовательно, оно будет иметь собственное распределение. Для случайной выборки п независимый наблюдения, ожидаемое значение выборочного среднего равно

${ displaystyle operatorname {E} ({ bar {x}}) = mu}$

и отклонение выборочного среднего составляет

${ displaystyle operatorname {var} ({ bar {x}}) = { frac { sigma ^ {2}} {n}}.}$

Если население нормально распределенный, то выборочное среднее обычно распределяется следующим образом:

${ displaystyle { bar {x}} Thicksim N left { mu, { frac { sigma ^ {2}} {n}} right }.}$

Если совокупность не имеет нормального распределения, среднее значение выборки, тем не менее, приблизительно нормально распределено, если п большой иσ²/п <+ ∞. Это следствие Центральная предельная теорема.

Смотрите также

• Основная тенденция
  • Медиана
  • Режим
• Описательная статистика
• Эксцесс
• Закон средних чисел
• Теорема о среднем значении
• Момент (математика)
• Сводные статистические данные
• Закон Тейлора

Примечания

Рекомендации