Обычный метод наименьших квадратов - Ordinary least squares

Часть серии по
Регрессивный анализ
Модели
Линейная регрессия Простая регрессия Полиномиальная регрессия Общая линейная модель
Обобщенная линейная модель Дискретный выбор Биномиальная регрессия Бинарная регрессия Логистическая регрессия Полиномиальный логит Смешанный логит Пробит Полиномиальный пробит Заказал логит Заказал пробит Пуассон
Многоуровневая модель Фиксированные эффекты Случайные эффекты Линейная модель смешанных эффектов Нелинейная модель смешанных эффектов
Нелинейная регрессия Непараметрический Полупараметрический Надежный Квантиль Изотонический Основные компоненты Наименьший угол Местный Сегментированный
Ошибки в переменных
Предварительный расчет
Наименьших квадратов Линейный Нелинейный
Обыкновенный Взвешенный Обобщенный
Частичное Всего Неотрицательный Регрессия хребта Регулярный
Наименьшие абсолютные отклонения Итеративно переназначенный Байесовский Байесовский многомерный
Задний план
Проверка регрессии Средний и прогнозируемый ответ Ошибки и остатки Доброту соответствия Студентизованный остаток Теорема Гаусса – Маркова
Математический портал

В статистика, обыкновенный метод наименьших квадратов (OLS) является разновидностью линейный метод наименьших квадратов метод оценки неизвестного параметры в линейная регрессия модель. OLS выбирает параметры линейная функция набора объясняющие переменные по принципу наименьших квадратов: минимизация суммы квадратов различий между наблюдаемыми зависимая переменная (значения наблюдаемой переменной) в данной набор данных и те, которые предсказываются линейной функцией.

Геометрически это рассматривается как сумма квадратов расстояний, параллельных оси зависимой переменной, между каждой точкой данных в наборе и соответствующей точкой на поверхности регрессии - чем меньше различия, тем лучше модель соответствует данным. . Результирующий оценщик можно выразить простой формулой, особенно в случае простая линейная регрессия, в котором есть одиночный регрессор в правой части уравнения регрессии.

МНК-оценка последовательный когда регрессоры экзогенный, и - Теорема Гаусса – Маркова —оптимальный в классе линейных несмещенных оценок когда ошибки находятся гомоскедастический и серийно некоррелированный. В этих условиях метод OLS обеспечивает минимальное отклонение среднее несмещенное оценка при конечных ошибках отклонения. При дополнительном предположении, что ошибки нормально распределенный, OLS - это оценщик максимального правдоподобия.

Линейная модель

Закон Окуня в макроэкономика утверждает, что в экономике рост ВВП должен линейно зависеть от изменений уровня безработицы. Здесь обычный метод наименьших квадратов используется для построения линии регрессии, описывающей этот закон.

Предположим, что данные состоят из п наблюдения { y_я, Икс_я }^п
_{я = 1}. Каждое наблюдение я включает скалярный ответ y_я и вектор-столбец Икс_я ценностей п параметры (регрессоры) Икс_ij для j = 1, ..., п. В модель линейной регрессии, переменная ответа, ${ displaystyle y_ {i}}$, является линейной функцией регрессоров:

${ displaystyle y_ {i} = beta _ {1} x_ {i1} + beta _ {2} x_ {i2} + cdots + beta _ {p} x_ {ip} + varepsilon _ {я},}$

или в вектор форма

${ displaystyle y_ {i} = mathbf {x} _ {i} ^ { mathsf {T}} { boldsymbol { beta}} + varepsilon _ {i}, ,}$

где Икс_я вектор-столбец яые наблюдения всех объясняющих переменных; ${ displaystyle { boldsymbol { beta}}}$ это п× 1 вектор неизвестных параметров; и скаляры ε_я представляют ненаблюдаемые случайные величины (ошибки ), которые учитывают влияние на ответы y_я из других источников, кроме пояснительных Икс_я. Эта модель также может быть записана в матричных обозначениях как

${ displaystyle mathbf {y} = mathrm {X} { boldsymbol { beta}} + { boldsymbol { varepsilon}}, ,}$

где y и ε находятся п× 1 векторы значений переменной отклика и ошибок для различных наблюдений, и Икс является п×п матрица регрессоров, также иногда называемая матрица дизайна, чья строка я является Икс_я^Т и содержит яые наблюдения по всем независимым переменным.

Как правило, постоянный член всегда входит в набор регрессоров. Икс, скажем, взяв Икс_я1 = 1 для всех я = 1, ..., п. Коэффициент β₁ соответствующий этому регрессору называется перехватить.

Регрессоры не обязательно должны быть независимыми: между регрессорами может быть любое желаемое отношение (при условии, что оно не является линейным). Например, мы можем подозревать, что ответ линейно зависит как от значения, так и от его квадрата; в этом случае мы должны включить один регрессор, значение которого равно квадрату другого регрессора. В этом случае модель будет квадратичный во втором регрессоре, но тем не менее считается линейный модель, потому что модель является по-прежнему линейна по параметрам (β).

Матричная / векторная формулировка

Рассмотрим сверхдетерминированная система

${ displaystyle sum _ {j = 1} ^ {p} X_ {ij} beta _ {j} = y_ {i}, (i = 1,2, dots, n),}$

из п линейные уравнения в п неизвестно коэффициенты, β₁, β₂, ..., β_п, с участием п > п. (Примечание: для линейной модели, как указано выше, не все Икс содержит информацию о точках данных. Первый столбец заполнен единицами, ${ displaystyle X_ {i1} = 1}$, только другие столбцы содержат фактические данные, поэтому здесь п = количество регрессоров + 1.) Это можно записать в матрица форма как

${ displaystyle mathrm {X} { boldsymbol { beta}} = mathbf {y},}$

где

${ displaystyle mathrm {X} = { begin {bmatrix} X_ {11} & X_ {12} & cdots & X_ {1p} X_ {21} & X_ {22} & cdots & X_ {2p} vdots & vdots & ddots & vdots X_ {n1} & X_ {n2} & cdots & X_ {np} end {bmatrix}}, qquad { boldsymbol { beta}} = { begin {bmatrix } beta _ {1} beta _ {2} vdots beta _ {p} end {bmatrix}}, qquad mathbf {y} = { begin {bmatrix} y_ { 1} y_ {2} vdots y_ {n} end {bmatrix}}.}$

Такая система обычно не имеет точного решения, поэтому цель состоит в том, чтобы найти коэффициенты ${ displaystyle { boldsymbol { beta}}}$ которые соответствуют уравнениям "наилучшим образом" в смысле решения квадратичный минимизация проблема

${ displaystyle { hat { boldsymbol { beta}}} = { underset { boldsymbol { beta}} { operatorname {arg , min}}} , S ({ boldsymbol { beta}} ),}$

где целевая функция S дан кем-то

${ displaystyle S ({ boldsymbol { beta}}) = sum _ {i = 1} ^ {n} { biggl |} y_ {i} - sum _ {j = 1} ^ {p} X_ {ij} beta _ {j} { biggr |} ^ {2} = { bigl |} mathbf {y} - mathrm {X} { boldsymbol { beta}} { bigr |} ^ {2}.}$

Обоснование выбора этого критерия приведено в Свойства ниже. Эта задача минимизации имеет уникальное решение при условии, что п столбцы матрицы Икс находятся линейно независимый, заданный путем решения нормальные уравнения

${ displaystyle ( mathrm {X} ^ { mathsf {T}} mathrm {X}) { hat { boldsymbol { beta}}} = mathrm {X} ^ { mathsf {T}} mathbf {y} .}$

Матрица ${ Displaystyle mathrm {X} ^ { mathsf {T}} mathrm {X}}$ известен как нормальная матрица и матрица ${ Displaystyle mathrm {X} ^ { mathsf {T}} mathbf {y}}$ известен как матрица моментов регресса и регрессорами.^[1] В заключение, ${ displaystyle { hat { boldsymbol { beta}}}}$ вектор коэффициентов наименьших квадратов гиперплоскость, выраженный как

${ displaystyle { hat { boldsymbol { beta}}} = left ( mathrm {X} ^ { mathsf {T}} mathrm {X} right) ^ {- 1} mathrm {X} ^ { mathsf {T}} mathbf {y}.}$

Предварительный расчет

Предположим б значение "кандидата" для вектора параметров β. Количество y_я − Икс_я^Тб, называется остаточный для я-е наблюдение, измеряет расстояние по вертикали между точками данных (Икс_я, y_я) и гиперплоскость y = Икс^Тб, и таким образом оценивает степень соответствия между фактическими данными и моделью. В сумма квадратов остатков (ССР) (также называемый сумма квадратов ошибок (ESS) или остаточная сумма квадратов (RSS))^[2] является мерой соответствия модели в целом:

${ Displaystyle S (b) = сумма _ {я = 1} ^ {n} (y_ {i} -x_ {i} ^ { mathrm {T}} b) ^ {2} = (y-Xb) ^ { mathrm {T}} (y-Xb),}$

где Т обозначает матрицу транспонировать, а ряды Икс, обозначающие значения всех независимых переменных, связанных с определенным значением зависимой переменной, являются Икс_я = х_я^Т. Значение б который минимизирует эту сумму, называется Оценщик OLS для β. Функция S(б) квадратично по б с положительно определенным Гессен, поэтому эта функция обладает единственным глобальным минимумом на ${ displaystyle b = { hat { beta}}}$, который может быть задан явной формулой:^{[3][доказательство]}

${ displaystyle { hat { beta}} = operatorname {argmin} _ {b in mathbb {R} ^ {p}} S (b) = (X ^ { mathrm {T}} X) ^ {-1} X ^ { mathrm {T}} y .}$

Продукт N=Икс^Т Икс это нормальная матрица и его обратное, Q=N^–1, это матрица кофакторов из β,^[4][5][6] тесно связан с его ковариационная матрица, C_β.Матрица (Икс^Т Икс)^–1 Икс^Т=Q Икс^Т называется Псевдообратная матрица Мура – ​​Пенроуза матрица X. Эта формулировка подчеркивает, что оценка может быть выполнена тогда и только тогда, когда не существует идеального мультиколлинеарность между независимыми переменными (что приведет к тому, что нормальная матрица не будет иметь обратной).

После того, как мы оценили β, то подогнанные значения (или прогнозируемые значения) от регрессии будет

${ displaystyle { hat {y}} = X { hat { beta}} = Py,}$

где п = Икс(Икс^ТИкс)⁻¹Икс^Т это матрица проекции в космос V покрытый столбцами Икс. Эта матрица п также иногда называют шляпа матрица потому что это "ставит шляпу" на переменную y. Другая матрица, тесно связанная с п это аннигилятор матрица M = я_п − п; это матрица проекции на пространство, ортогональное V. Обе матрицы п и M находятся симметричный и идемпотент (означающий, что п² = п и M² = M), и относятся к матрице данных Икс через личности PX = Икс и MX = 0.^[7] Матрица M создает остатки из регрессии:

${ displaystyle { hat { varepsilon}} = y - { hat {y}} = yX { hat { beta}} = My = M (X beta + varepsilon) = (MX) beta + M varepsilon = M varepsilon.}$

Используя эти невязки, мы можем оценить значение σ ² с использованием уменьшенный хи-квадрат статистика:

${ displaystyle s ^ {2} = { frac {{ hat { varepsilon}} ^ { mathrm {T}} { hat { varepsilon}}} {np}} = { frac {(My) ^ { mathrm {T}} My} {np}} = { frac {y ^ { mathrm {T}} M ^ { mathrm {T}} My} {np}} = { frac {y ^ { mathrm {T}} My} {np}} = { frac {S ({ hat { beta}})} {np}}, qquad { hat { sigma}} ^ {2} = { frac {np} {n}} ; s ^ {2}}$

Знаменатель, п−п, это статистические степени свободы. Первое количество, s², - оценка МНК для σ², а второй ${ displaystyle scriptstyle { hat { sigma}} ^ {2}}$, - оценка MLE для σ². Эти две оценки очень похожи в больших выборках; первая оценка всегда беспристрастный, а вторая оценка смещена, но имеет меньшую среднеквадратичная ошибка. На практике s² используется чаще, так как это удобнее для проверки гипотез. Квадратный корень из s² называется стандартная ошибка регрессии,^[8] стандартная ошибка регрессии,^[9][10] или стандартная ошибка уравнения.^[7]

Обычно степень согласия регрессии МНК обычно оценивают путем сравнения того, насколько первоначальная вариация в выборке может быть уменьшена путем регрессии на Икс. В коэффициент детерминации р² определяется как отношение «объясненной» дисперсии к «общей» дисперсии зависимой переменной. y, в тех случаях, когда сумма квадратов регрессии равна сумме квадратов остатков:^[11]

${ displaystyle R ^ {2} = { frac { sum ({ hat {y}} _ {i} - { overline {y}}) ^ {2}} { sum (y_ {i} - { overline {y}}) ^ {2}}} = { frac {y ^ { mathrm {T}} P ^ { mathrm {T}} LPy} {y ^ { mathrm {T}} Ly }} = 1 - { frac {y ^ { mathrm {T}} My} {y ^ { mathrm {T}} Ly}} = 1 - { frac { rm {RSS}} { rm { TSS}}}}$

где TSS - общая сумма квадратов для зависимой переменной, L = я_п − 11^Т/ п, и 1 является п× 1 вектор единиц. (L является «центрирующей матрицей», которая эквивалентна регрессии по константе; он просто вычитает среднее значение из переменной.) р² чтобы иметь смысл, матрица Икс данных о регрессорах должен содержать вектор-столбец из единиц для представления константы, коэффициент которой является точкой пересечения регрессии. В этом случае, р² всегда будет числом от 0 до 1, а значения, близкие к 1, указывают на хорошую степень соответствия.

Дисперсия прогноза независимой переменной как функции зависимой переменной приведена в статье. Полиномиальные наименьшие квадраты.

Модель простой линейной регрессии

Если матрица данных Икс содержит только две переменные, константу и скалярный регрессор Икс_я, то это называется «простой регрессионной моделью».^[12] Этот случай часто рассматривается в классах статистики для начинающих, поскольку он предоставляет гораздо более простые формулы, подходящие даже для ручного расчета. Параметры обычно обозначаются как (α, β):

${ displaystyle y_ {i} = alpha + beta x_ {i} + varepsilon _ {i}.}$

Оценки наименьших квадратов в этом случае даются простыми формулами

${ displaystyle { begin {align} { hat { beta}} & = { frac { sum {x_ {i} y_ {i}} - { frac {1} {n}} sum {x_ {i}} sum {y_ {i}}} { sum {x_ {i} ^ {2}} - { frac {1} {n}} ( sum {x_ {i}}) ^ {2 }}} = { frac { operatorname {Cov} [x, y]} { operatorname {Var} [x]}} { hat { alpha}} & = { overline {y}} - { hat { beta}} , { overline {x}} , end {выравнивается}}}$

где Var (.) и Cov (.) - параметры выборки.

Альтернативные производные

В предыдущем разделе оценщик наименьших квадратов ${ displaystyle { hat { beta}}}$ был получен как значение, которое минимизирует сумму квадратов остатков модели. Однако можно получить такую ​​же оценку и из других подходов. Во всех случаях формула для оценки МНК остается прежней: ^{^}β = (Икс^ТИкс)⁻¹Икс^Тy; единственная разница в том, как мы интерпретируем этот результат.

Проекция

МНК-оценку можно рассматривать как проекцию на линейное пространство, охватываемое регрессорами. (Здесь каждый из ${ displaystyle X_ {1}}$ и ${ displaystyle X_ {2}}$ относится к столбцу матрицы данных.)

Возможно, этот раздел необходимо очистить. Он был объединен с Линейный метод наименьших квадратов (математика).

Для математиков OLS - это приближенное решение переопределенной системы линейных уравнений. Xβ ≈ y, где β это неизвестное. Если предположить, что система не может быть решена точно (количество уравнений п намного больше, чем количество неизвестных п), мы ищем решение, которое могло бы обеспечить наименьшее расхождение между правой и левой частями. Другими словами, мы ищем решение, удовлетворяющее

${ displaystyle { hat { beta}} = { rm {arg}} min _ { beta} , lVert y-X beta rVert,}$

где || · || это стандарт L² норма в п-размерный Евклидово пространство р^п. Прогнозируемое количество Xβ есть некая линейная комбинация векторов регрессоров. Таким образом, остаточный вектор y − Xβ будет иметь наименьшую длину, когда y является проецируется ортогонально на линейное подпространство охватывал колоннами Икс. Оценщик OLS ${ displaystyle { hat { beta}}}$ в этом случае можно интерпретировать как коэффициенты векторное разложение из ^{^}y = Py на основе Икс.

Другими словами, уравнения градиента по минимуму можно записать как:

${ displaystyle ( mathbf {y} -X { hat { boldsymbol { beta}}}) ^ { rm {T}} X = 0.}$

Геометрическая интерпретация этих уравнений состоит в том, что вектор невязок, ${ displaystyle mathbf {y} -X { hat { boldsymbol { beta}}}}$ ортогонален пространство столбца из Икс, поскольку скалярное произведение ${ displaystyle ( mathbf {y} -X { hat { boldsymbol { beta}}}) cdot X mathbf {v}}$ равен нулю для Любые конформный вектор, v. Это значит, что ${ displaystyle mathbf {y} -X { boldsymbol { hat { beta}}}}$ самый короткий из всех возможных векторов ${ displaystyle mathbf {y} -X { boldsymbol { beta}}}$, то есть дисперсия остатков минимально возможна. Это показано справа.

Представляем ${ displaystyle { hat { boldsymbol { gamma}}}}$ и матрица K в предположении, что матрица ${ Displaystyle [Х К]}$ неособен и K^Т Икс = 0 (ср. Ортогональные проекции ), остаточный вектор должен удовлетворять следующему уравнению:

${ displaystyle { hat { mathbf {r}}} треугольник mathbf {y} -X { hat { boldsymbol { beta}}} = K { hat { boldsymbol { gamma}}}. }$

Таким образом, уравнение и решение линейных наименьших квадратов описываются следующим образом:

${ displaystyle mathbf {y} = { begin {bmatrix} X&K end {bmatrix}} { begin {pmatrix} { hat { boldsymbol { beta}}} { hat { boldsymbol { гамма}}} end {pmatrix}},}$

${ displaystyle { begin {pmatrix} { hat { boldsymbol { beta}}} { hat { boldsymbol { gamma}}} end {pmatrix}} = { begin {bmatrix} X&K конец {bmatrix}} ^ {- 1} mathbf {y} = { begin {bmatrix} (X ^ { rm {T}} X) ^ {- 1} X ^ { rm {T}} (K ^ { rm {T}} K) ^ {- 1} K ^ { rm {T}} end {bmatrix}} mathbf {y}.}$

Другой способ взглянуть на это - рассматривать линию регрессии как средневзвешенное значение линий, проходящих через комбинацию любых двух точек в наборе данных.^[13] Хотя этот способ расчета более затратен с точки зрения вычислений, он обеспечивает лучшую интуицию на OLS.

Максимальная вероятность

Оценщик OLS идентичен оценке оценщик максимального правдоподобия (MLE) в предположении нормальности для ошибок.^{[14][доказательство]} Это предположение о нормальности имеет историческое значение, поскольку оно послужило основой для ранних работ в области линейного регрессионного анализа. Йоль и Пирсон.^{[нужна цитата ]} Из свойств MLE мы можем сделать вывод, что оценка OLS асимптотически эффективна (в смысле достижения Граница Крамера – Рао для дисперсии), если выполняется предположение о нормальности.^[15]

Обобщенный метод моментов

В iid случае МНК-оценку также можно рассматривать как GMM оценка, возникающая из моментных условий

${ displaystyle mathrm {E} { big [} , x_ {i} (y_ {i} -x_ {i} ^ {T} beta) , { big]} = 0.}$

Эти моментные условия утверждают, что регрессоры не должны коррелировать с ошибками. поскольку Икс_я это п-вектор, количество моментных состояний равно размерности вектора параметров β, и таким образом система точно идентифицирована. Это так называемый классический случай GMM, когда оценка не зависит от выбора весовой матрицы.

Обратите внимание, что исходное строгое предположение экзогенности E [ε_я | Икс_я] = 0 подразумевает гораздо более богатый набор моментных условий, чем указано выше. В частности, из этого предположения следует, что для любой вектор-функции ƒ, моментное условие E [ƒ(Икс_я)·ε_я] = 0 будет держать. Однако это можно показать с помощью Теорема Гаусса – Маркова что оптимальный выбор функции ƒ должен взять ƒ(Икс) = Икс, что приводит к приведенному выше уравнению момента.

Свойства

Предположения

Есть несколько различных структур, в которых модель линейной регрессии может быть отлит, чтобы применить технику OLS. Каждый из этих параметров дает одинаковые формулы и одинаковые результаты. Единственная разница заключается в интерпретации и допущениях, которые должны быть наложены, чтобы метод дал значимые результаты. Выбор применяемой структуры зависит главным образом от природы имеющихся данных и от задачи вывода, которую необходимо выполнить.

Одна из линий разницы в интерпретации заключается в том, следует ли рассматривать регрессоры как случайные величины или как предопределенные константы. В первом случае (случайный дизайн) регрессоры Икс_я являются случайными и отбираются вместе с y_яиз некоторых Население, как в наблюдательное исследование. Такой подход позволяет более естественным образом изучить асимптотические свойства оценщиков. В другой интерпретации (фиксированный дизайн), регрессоры Икс рассматриваются как известные константы, установленные дизайн, и y отбирается условно по значениям Икс как в эксперимент. Для практических целей это различие часто не имеет значения, поскольку оценка и логический вывод выполняются, пока Икс. Все результаты, изложенные в этой статье, находятся в рамках случайного проектирования.

Классическая модель линейной регрессии

Классическая модель фокусируется на оценке и выводе "конечной выборки", что означает, что количество наблюдений п фиксированный. Это контрастирует с другими подходами, изучающими асимптотическое поведение OLS, и в котором количество наблюдений может расти до бесконечности.

• Правильная спецификация. Линейная функциональная форма должна совпадать с формой фактического процесса генерации данных.
• Строгая экзогенность. Ошибки в регрессии должны иметь условное среднее нуль:^[16]

  ${ displaystyle operatorname {E} [, varepsilon mid X ,] = 0.}$

Непосредственным следствием предположения об экзогенности является то, что ошибки имеют нулевое среднее значение: E [ε] = 0, и что регрессоры не коррелируют с ошибками: E [Икс^Тε] = 0.

Предположение экзогенности имеет решающее значение для теории OLS. Если это так, переменные регрессора называются экзогенный. Если это не так, то те регрессоры, которые коррелируют с ошибкой, называются эндогенный,^[17] и тогда оценки OLS становятся недействительными. В таком случае метод инструментальных переменных может использоваться для вывода.

• Нет линейной зависимости. Регрессоры в Икс все должно быть линейно независимый. Математически это означает, что матрица Икс должен иметь полный ранг столбца почти наверняка:^[18]

  ${ displaystyle Pr ! { big [} , operatorname {rank} (X) = p , { big]} = 1.}$

Обычно также предполагается, что регрессоры имеют конечные моменты, по крайней мере, до второго момента. Тогда матрица Q_хх = E [Икс^ТИкс / п] конечно и положительно полуопределенно.

Когда это предположение нарушается, регрессоры называют линейно зависимыми или идеально мультиколлинеарен. В таком случае значение коэффициента регрессии β невозможно узнать, хотя предсказание y values ​​все еще возможен для новых значений регрессоров, которые лежат в том же линейно зависимом подпространстве.

• Сферические ошибки:^[18]

  ${ displaystyle operatorname {Var} [, varepsilon mid X ,] = sigma ^ {2} I_ {n},}$

где я_п это единичная матрица в измерении п, и σ² - параметр, определяющий дисперсию каждого наблюдения. Эта σ² считается неприятный параметр в модели, хотя обычно и оценивается. Если это предположение нарушается, то оценки OLS по-прежнему действительны, но уже неэффективны.

Это предположение принято разделять на две части:

• Гомоскедастичность: E [ε_я² | Икс ] = σ², что означает, что член ошибки имеет такую ​​же дисперсию σ² в каждом наблюдении. Когда это требование нарушается, это называется гетероскедастичность, в таком случае более эффективная оценка была бы взвешенный метод наименьших квадратов. Если ошибки имеют бесконечную дисперсию, то оценки OLS также будут иметь бесконечную дисперсию (хотя закон больших чисел они, тем не менее, будут стремиться к истинным значениям, пока ошибки имеют нулевое среднее). В таком случае, робастная оценка рекомендуются техники.
• Нет автокорреляция: ошибки некоррелированный между наблюдениями: E [ε_яε_j | Икс ] = 0 для я ≠ j. Это предположение может быть нарушено в контексте Временные ряды данные, данные панели, кластерные выборки, иерархические данные, данные повторных измерений, продольные данные и другие данные с зависимостями. В таких случаях обобщенный метод наименьших квадратов обеспечивает лучшую альтернативу, чем OLS. Еще одно выражение для автокорреляции: серийная корреляция.

• Нормальность. Иногда дополнительно предполагают, что ошибки имеют нормальное распределение условно от регрессоров:^[19]

  ${ displaystyle varepsilon mid X sim { mathcal {N}} (0, sigma ^ {2} I_ {n}).}$

Это предположение не требуется для достоверности метода OLS, хотя некоторые дополнительные свойства конечной выборки могут быть установлены в том случае, если это произойдет (особенно в области проверки гипотез). Также, когда ошибки нормальные, оценка МНК эквивалентна оценке оценщик максимального правдоподобия (MLE), поэтому он асимптотически эффективен в классе всех регулярные оценщики. Важно отметить, что предположение о нормальности применимо только к ошибочным членам; вопреки распространенному заблуждению, переменная ответа (зависимая) не обязательно должна иметь нормальное распределение.^[20]

Независимые и одинаково распределенные (iid)

В некоторых приложениях, особенно с данные поперечного сечения, накладывается дополнительное предположение - что все наблюдения независимы и одинаково распределены. Это означает, что все наблюдения взяты из случайный пример что упрощает все перечисленные ранее допущения и облегчает их интерпретацию. Также эта структура позволяет сформулировать асимптотические результаты (поскольку размер выборки п → ∞), которые понимаются как теоретическая возможность получения новых независимых наблюдений из процесс генерации данных. Список предположений в этом случае:

• iid наблюдения: (Икс_я, y_я) является независимый из, и имеет то же самое распространение так как, (Икс_j, y_j) для всех я ≠ j;
• нет идеальной мультиколлинеарности: Q_хх = E [Икс_я Икс_я^Т ] это положительно определенная матрица;
• экзогенность: E [ε_я | Икс_я ] = 0;
• гомоскедастичность: Вар [ε_я | Икс_я ] = σ².

Модель временного ряда

• В случайный процесс {Икс_я, y_я} является стационарный и эргодический; если {Икс_я, y_я} нестационарен, результаты OLS часто бывают ложными, если {Икс_я, y_я} является совместная интеграция.
• Регрессоры предопределенный: E [Икс_яε_я] = 0 для всех я = 1, ..., п;
• В п×п матрица Q_хх = E [Икс_я Икс_я^Т ] имеет полный ранг, а значит положительно определенный;
• {Икс_яε_я} это последовательность разностей мартингалов, с конечной матрицей вторых моментов Q_xxε² = E [ε_я²Икс_я Икс_я^Т ].

Свойства конечного образца

Прежде всего, под строгая экзогенность предположить, что оценки МНК ${ displaystyle scriptstyle { hat { beta}}}$ и s² находятся беспристрастный, что означает, что их ожидаемые значения совпадают с истинными значениями параметров:^{[21][доказательство]}

${ displaystyle operatorname {E} [, { hat { beta}} mid X ,] = beta, quad operatorname {E} [, s ^ ​​{2} mid X ,] = sigma ^ {2}.}$

Если строгая экзогенность не выполняется (как в случае со многими Временные ряды модели, где экзогенность предполагается только в отношении прошлых шоков, но не будущих), то эти оценки будут смещены в конечных выборках.

В ковариационная матрица (или просто ковариационная матрица) из ${ displaystyle scriptstyle { hat { beta}}}$ равно^[22]

${ displaystyle operatorname {Var} [, { hat { beta}} mid X ,] = sigma ^ {2} (X ^ {T} X) ^ {- 1} = sigma ^ { 2} Q.}$

В частности, стандартная ошибка каждого коэффициента ${ displaystyle scriptstyle { hat { beta}} _ {j}}$ равен квадратному корню из j-й диагональный элемент этой матрицы. Оценка этой стандартной ошибки получается заменой неизвестной величины σ² со своей оценкой s². Таким образом,

${ displaystyle { widehat { operatorname {s. ! e.}}} ({ hat { beta}} _ {j}) = { sqrt {s ^ {2} (X ^ {T} X ) _ {jj} ^ {- 1}}}}$

Также легко показать, что оценка ${ displaystyle scriptstyle { hat { beta}}}$ не коррелирует с остатками из модели:^[22]

${ displaystyle operatorname {Cov} [, { hat { beta}}, { hat { varepsilon}} mid X ,] = 0.}$

В Теорема Гаусса – Маркова заявляет, что под сферические ошибки предположение (то есть ошибки должны быть некоррелированный и гомоскедастический ) оценщик ${ displaystyle scriptstyle { hat { beta}}}$ эффективен в классе линейных несмещенных оценок. Это называется лучшая линейная несмещенная оценка (СИНИЙ). Эффективность следует понимать так, как если бы мы хотели найти какую-то другую оценку. ${ displaystyle scriptstyle { tilde { beta}}}$ который был бы линейным по y и беспристрастно, то ^[22]

${ displaystyle operatorname {Var} [, { tilde { beta}} mid X ,] - operatorname {Var} [, { hat { beta}} mid X ,] geq 0}$

в том смысле, что это неотрицательно-определенная матрица. Эта теорема устанавливает оптимальность только в классе линейных несмещенных оценок, что весьма ограничительно. В зависимости от распределения ошибок ε, другие, нелинейные оценки могут дать лучшие результаты, чем OLS.

Предполагая нормальность

Все перечисленные до сих пор свойства действительны независимо от основного распределения условий ошибки. Однако если вы готовы предположить, что предположение о нормальности выполняется (то есть ε ~ N(0, σ²я_п)), то можно указать дополнительные свойства МНК-оценок.

Оценщик ${ displaystyle scriptstyle { hat { beta}}}$ имеет нормальное распределение со средним значением и дисперсией, как указано выше:^[23]

${ displaystyle { hat { beta}} sim { mathcal {N}} { big (} beta, sigma ^ {2} (X ^ { mathrm {T}} X) ^ {-1} { big)}}$

где Q это матрица кофакторов. Эта оценка достигает Граница Крамера – Рао для модели и, таким образом, оптимален в классе всех несмещенных оценок.^[15] Обратите внимание, что в отличие от Теорема Гаусса – Маркова, этот результат устанавливает оптимальность как линейных, так и нелинейных оценок, но только в случае нормально распределенных членов ошибки.

Оценщик s² будет пропорционально распределение хи-квадрат:^[24]

${ Displaystyle s ^ {2} sim { frac { sigma ^ {2}} {n-p}} cdot chi _ {n-p} ^ {2}}$

Дисперсия этой оценки равна 2σ⁴/(п − п), который не достигает Граница Крамера – Рао из 2σ⁴/п. Однако было показано, что объективных оценок σ² с дисперсией меньше, чем у оценки s².^[25] Если мы готовы допустить предвзятые оценки и рассмотреть класс оценок, которые пропорциональны сумме квадратов остатков (SSR) модели, то лучший (в смысле среднеквадратичная ошибка ) оценщик в этом классе будет ^~σ² = SSR/ (п − п + 2), что даже превосходит границу Крамера – Рао в случае, когда имеется только один регрессор (п = 1).^[26]

Более того, оценщики ${ displaystyle scriptstyle { hat { beta}}}$ и s² находятся независимый,^[27] факт, который пригодится при построении t- и F-тестов для регрессии.

Влиятельные наблюдения

Как упоминалось ранее, оценщик ${ displaystyle { hat { beta}}}$ линейно по y, что означает, что он представляет собой линейную комбинацию зависимых переменных y_я. Веса в этой линейной комбинации являются функциями регрессоров Икс, и, как правило, неравны. Наблюдения с большим весом называются влиятельный потому что они имеют более выраженное влияние на значение оценщика.

Чтобы проанализировать, какие наблюдения имеют большое значение, мы удаляем конкретный j-е наблюдение и подумайте, насколько изменятся расчетные количества (аналогично складной нож ). Можно показать, что изменение оценки МНК для β будет равно ^[28]

${ displaystyle { hat { beta}} ^ {(j)} - { hat { beta}} = - { frac {1} {1-h_ {j}}} (X ^ { mathrm { T}} X) ^ {- 1} x_ {j} ^ { mathrm {T}} { hat { varepsilon}} _ {j} ,,}$

где час_j = Икс_j^Т (Икс^ТИкс)⁻¹Икс_j это j-й диагональный элемент матрицы шляпы п, и Икс_j - вектор регрессоров, соответствующий j-е наблюдение. Аналогичным образом изменение прогнозируемого значения для j-е наблюдение в результате исключения этого наблюдения из набора данных будет равно ^[28]

${ displaystyle { hat {y}} _ {j} ^ {(j)} - { hat {y}} _ {j} = x_ {j} ^ { mathrm {T}} { hat { beta}} ^ {(j)} - x_ {j} ^ {T} { hat { beta}} = - { frac {h_ {j}} {1-h_ {j}}} , { шляпа { varepsilon}} _ {j}}$

Из свойств матрицы шляпы, 0 ≤ час_j ≤ 1, и они суммируют п, так что в среднем час_j ≈ п / п. Эти количества час_j называются рычаги, и наблюдения с высоким час_j называются точки кредитного плеча.^[29] Обычно наблюдения с большим кредитным плечом должны быть изучены более тщательно, если они ошибочны, выпадают или каким-либо иным образом нетипичны для остальной части набора данных.

Разделенная регрессия

Иногда переменные и соответствующие параметры в регрессии можно логически разделить на две группы, так что регрессия принимает вид

${ displaystyle y = X_ {1} beta _ {1} + X_ {2} beta _ {2} + varepsilon,}$

где Икс₁ и Икс₂ иметь размеры п×п₁, п×п₂, и β₁, β₂ находятся п₁× 1 и п₂× 1 векторов, с п₁ + п₂ = п.

В Теорема Фриша – Во – Ловелла. утверждает, что в этой регрессии остатки ${ displaystyle { hat { varepsilon}}}$ и оценка МНК ${ displaystyle scriptstyle { hat { beta}} _ {2}}$ будут численно идентичны остаткам и оценке МНК для β₂ в следующей регрессии:^[30]

${ Displaystyle M_ {1} y = M_ {1} X_ {2} beta _ {2} + eta ,,}$

где M₁ это аннигиляторная матрица для регрессоров Икс₁.

Теорема может быть использована для получения ряда теоретических результатов. Например, наличие регрессии с константой и другим регрессором эквивалентно вычитанию средних значений из зависимой переменной и регрессора и последующему запуску регрессии для переменных без значения, но без постоянного члена.

Ограниченная оценка

Предположим, известно, что коэффициенты регрессии удовлетворяют системе линейных уравнений

${ Displaystyle A двоеточие quad Q ^ {T} beta = c, ,}$

где Q это п×q матрица полного ранга, и c это q× 1 вектор известных констант, где д <р. В этом случае оценка методом наименьших квадратов эквивалентна минимизации суммы квадратов остатков модели с учетом ограничения А. В метод наименьших квадратов с ограничениями (CLS) оценка может быть дана явной формулой:^[31]

${ displaystyle { hat { beta}} ^ {c} = { hat { beta}} - (X ^ {T} X) ^ {- 1} Q { Big (} Q ^ {T} ( X ^ {T} X) ^ {- 1} Q { Big)} ^ {- 1} (Q ^ {T} { hat { beta}} - c).}$

Это выражение для оценки с ограничениями действительно до тех пор, пока матрица Икс^ТИкс обратимо. С самого начала этой статьи предполагалось, что эта матрица имеет полный ранг, и было отмечено, что, когда условие ранга не выполняется, β не будет идентифицирован. Однако может случиться так, что добавление ограничения А делает β идентифицируемый, и в этом случае нужно найти формулу для оценки. Оценщик равен ^[32]

${ displaystyle { hat { beta}} ^ {c} = R (R ^ {T} X ^ {T} XR) ^ {- 1} R ^ {T} X ^ {T} y + { Big ( } I_ {p} -R (R ^ {T} X ^ {T} XR) ^ {- 1} R ^ {T} X ^ {T} X { Big)} Q (Q ^ {T} Q) ^ {- 1} c,}$

где р это п×(п − q) матрица такая, что матрица [Q R] неособен, и р^ТQ = 0. Такую матрицу всегда можно найти, хотя в целом она не уникальна. Вторая формула совпадает с первой в случае, когда Икс^ТИкс обратимо.^[32]

Свойства большого образца

Оценщики наименьших квадратов: точечные оценки параметров модели линейной регрессии β. Однако обычно мы также хотим знать, насколько близки эти оценки к истинным значениям параметров. Другими словами, мы хотим построить интервальные оценки.

Поскольку мы не делали никаких предположений о распределении ошибки ε_я, невозможно вывести распределение оценок ${ displaystyle { hat { beta}}}$ и ${ Displaystyle { шляпа { sigma}} ^ {2}}$. Тем не менее, мы можем применить Центральная предельная теорема вывести их асимптотический свойства как размер выборки п уходит в бесконечность. Хотя размер выборки обязательно конечен, принято считать, что п является «достаточно большим», так что истинное распределение оценки OLS близко к его асимптотическому пределу.

Можно показать, что в предположениях модели оценка методом наименьших квадратов для β является последовательный (это ${ displaystyle { hat { beta}}}$ сходится по вероятности к β) и асимптотически нормально:^{[доказательство]}

${ displaystyle ({ hat { beta}} - beta) { xrightarrow {d}} { mathcal {N}} { big (} 0, ; sigma ^ {2} Q_ {xx } ^ {- 1} { big)},}$

где ${ displaystyle Q_ {xx} = X ^ {T} X.}$

Интервалы

Используя это асимптотическое распределение, приблизьте двусторонние доверительные интервалы для j-я компонента вектора ${ displaystyle { hat { beta}}}$ можно построить как

${ displaystyle beta _ {j} in { bigg [} { hat { beta}} _ {j} pm q_ {1 - { frac { alpha} {2}}} ^ {{ mathcal {N}} (0,1)} ! { sqrt {{ hat { sigma}} ^ {2} left [Q_ {xx} ^ {- 1} right] _ {jj}} } { bigg]}}$ на 1 − α уровень уверенности,

где q обозначает квантильная функция стандартного нормального распределения и [·]_jj это j-й диагональный элемент матрицы.

Аналогично, оценка методом наименьших квадратов для σ² также непротиворечиво и асимптотически нормально (при условии, что четвертый момент ε_я существует) с предельным распределением

${ displaystyle ({ hat { sigma}} ^ {2} - sigma ^ {2}) { xrightarrow {d}} { mathcal {N}} left (0, ; operatorname { E} left [ varepsilon _ {i} ^ {4} right] - sigma ^ {4} right).}$

Эти асимптотические распределения можно использовать для прогнозирования, проверки гипотез, построения других оценок и т. Д. В качестве примера рассмотрим проблему прогнозирования. Предположим ${ displaystyle x_ {0}}$ это некоторая точка в области распределения регрессоров, и нужно знать, какой была бы переменная ответа в этой точке. В средний ответ это количество ${ displaystyle y_ {0} = x_ {0} ^ { mathrm {T}} beta}$, тогда как предсказанный ответ является ${ displaystyle { hat {y}} _ {0} = x_ {0} ^ { mathrm {T}} { hat { beta}}}$. Очевидно, что прогнозируемый ответ является случайной величиной, его распределение может быть получено из распределения ${ displaystyle { hat { beta}}}$:

${ displaystyle left ({ hat {y}} _ {0} -y_ {0} right) { xrightarrow {d}} { mathcal {N}} left (0, ; sigma ^ {2} x_ {0} ^ { mathrm {T}} Q_ {xx} ^ {- 1} x_ {0} right),}$

что позволяет построить доверительные интервалы для среднего ответа ${ displaystyle y_ {0}}$ будут построены:

${ displaystyle y_ {0} in left [ x_ {0} ^ { mathrm {T}} { hat { beta}} pm q_ {1 - { frac { alpha} {2}} } ^ {{ mathcal {N}} (0,1)} ! { sqrt {{ hat { sigma}} ^ {2} x_ {0} ^ { mathrm {T}} Q_ {xx} ^ {- 1} x_ {0}}} right]}$ на 1 − α уровень уверенности.

Проверка гипотезы

Эта секция нуждается в расширении. Вы можете помочь добавляя к этому. (Февраль 2017 г.)

Особенно широко используются две проверки гипотез. Во-первых, кто-то хочет знать, лучше ли оценочное уравнение регрессии, чем простое предсказание, что все значения переменной ответа равны ее выборочному среднему (если нет, то говорят, что оно не имеет объяснительной силы). В нулевая гипотеза отсутствие объяснительной ценности оцененной регрессии проверяется с использованием F-тест. Если вычисленное F-значение оказывается достаточно большим, чтобы превысить свое критическое значение для предварительно выбранного уровня значимости, нулевая гипотеза отклоняется и Альтернативная гипотеза, что регрессия имеет объяснительную силу, принимается. В противном случае принимается нулевая гипотеза об отсутствии объяснительной силы.

Во-вторых, для каждой интересующей объясняющей переменной нужно знать, значительно ли отличается ее оценочный коэффициент от нуля, то есть действительно ли эта конкретная независимая переменная имеет объяснительную силу при прогнозировании переменной отклика. Здесь нулевая гипотеза состоит в том, что истинный коэффициент равен нулю. Эта гипотеза проверяется вычислением коэффициента t-статистика, как отношение оценки коэффициента к его стандартная ошибка. Если t-статистика больше заданного значения, нулевая гипотеза отклоняется, и выясняется, что переменная имеет объяснительную силу, а ее коэффициент значительно отличается от нуля. В противном случае принимается нулевая гипотеза о нулевом значении истинного коэффициента.

В дополнение Чау-тест используется для проверки того, имеют ли две подвыборки одинаковые истинные значения коэффициентов. Сумма квадратов остатков регрессий для каждого из подмножеств и для объединенного набора данных сравнивается путем вычисления F-статистики; если это превышает критическое значение, нулевая гипотеза об отсутствии разницы между двумя подмножествами отклоняется; в противном случае принимается.

Пример с реальными данными

Диаграмма рассеяния данных, связь слегка изогнута, но близка к линейной

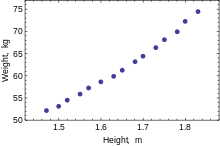
Следующий набор данных дает средние показатели роста и веса для американских женщин в возрасте 30–39 лет (источник: Всемирный альманах и книга фактов, 1975 г.).

Высота (м)	1.47	1.50	1.52	1.55	1.57	1.60	1.63	1.65	1.68	1.70	1.73	1.75	1.78	1.80	1.83
Вес (кг)	52.21	53.12	54.48	55.84	57.20	58.57	59.93	61.29	63.11	64.47	66.28	68.10	69.92	72.19	74.46

Когда моделируется только одна зависимая переменная, диаграмма рассеяния предложит форму и силу связи между зависимой переменной и регрессорами. Он также может выявить выбросы, гетероскедастичность и другие аспекты данных, которые могут усложнить интерпретацию подобранной регрессионной модели. Диаграмма рассеяния предполагает, что связь сильная и может быть аппроксимирована квадратичной функцией. OLS может обрабатывать нелинейные отношения, вводя регрессор РОСТ². Затем регрессионная модель становится множественной линейной моделью:

${ displaystyle w_ {i} = beta _ {1} + beta _ {2} h_ {i} + beta _ {3} h_ {i} ^ {2} + varepsilon _ {i}.}$

Подходящая регрессия

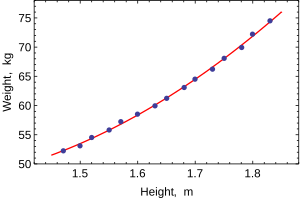
Вывод из самых популярных статистические пакеты будет выглядеть примерно так:

Метод	Наименьших квадратов
Зависимая переменная	ВЕС
Наблюдения	15
Параметр	Ценность	Стандартная ошибка	t-статистика	p-значение
${ displaystyle beta _ {1}}$	128.8128	16.3083	7.8986	0.0000
${ displaystyle beta _ {2}}$	–143.1620	19.8332	–7.2183	0.0000
${ displaystyle beta _ {3}}$	61.9603	6.0084	10.3122	0.0000
р2	0.9989	S.E. регресса		0.2516
Скорректированный R2	0.9987	Сумма кв.		692.61
Логарифмическая вероятность	1.0890	Остаточная сумма кв.		0.7595
Стат. Дурбина – Ватсона.	2.1013	Общая сумма кв.		693.37
Критерий Акаике	0.2548	F-статистика		5471.2
Критерий Шварца	0.3964	p-значение (F-stat)		0.0000

В этой таблице:

• В Ценность столбец дает оценки параметров методом наименьших квадратов β_j
• В Стандартная ошибка столбец показывает стандартные ошибки оценки каждого коэффициента: ${ displaystyle { hat { sigma}} _ {j} = left ({ hat { sigma}} ^ {2} left [Q_ {xx} ^ {- 1} right] _ {jj} right) ^ { frac {1} {2}}}$
• В t-статистика и p-значение столбцы проверяют, может ли какой-либо из коэффициентов быть равным нулю. В т-статистика рассчитывается просто как ${ Displaystyle т = { шляпа { бета}} _ {j} / { шляпа { sigma}} _ {j}}$. Если ошибки ε подчиняются нормальному распределению, т следует распределению Стьюдента. В более слабых условиях т асимптотически нормально. Большие значения т указывают, что нулевая гипотеза может быть отклонена и что соответствующий коэффициент не равен нулю.Второй столбец, п-ценность, выражает результаты проверки гипотезы как уровень значимости. Обычно п-значения меньше 0,05 принимаются как свидетельство того, что коэффициент генеральной совокупности не равен нулю.
• R-квадрат это коэффициент детерминации что указывает на соответствие регрессии. Эта статистика будет равна единице, если соответствие идеальное, и нулю, если регрессоры Икс не имеют никакой объяснительной силы. Это необъективная оценка населения. R-квадрат, и никогда не уменьшится при добавлении дополнительных регрессоров, даже если они не имеют значения.
• Скорректированный R-квадрат это слегка измененная версия ${ displaystyle R ^ {2}}$, предназначенная для наказания за избыточное количество регрессоров, которые не увеличивают объяснительную силу регрессии. Эта статистика всегда меньше, чем ${ displaystyle R ^ {2}}$, может уменьшаться при добавлении новых регрессоров и даже быть отрицательным для плохо подходящих моделей:

${ displaystyle { overline {R}} ^ {2} = 1 - { frac {n-1} {n-p}} (1-R ^ {2})}$

• Логарифмическая вероятность рассчитывается в предположении, что ошибки подчиняются нормальному распределению. Несмотря на то, что это предположение не очень разумно, эта статистика все же может найти свое применение при проведении LR-тестов.
• Статистика Дарбина – Ватсона проверяет, есть ли какие-либо доказательства серийной корреляции между остатками. Как показывает практика, значение меньше 2 будет свидетельством положительной корреляции.
• Информационный критерий Акаике и Критерий Шварца оба используются для выбора модели. Обычно при сравнении двух альтернативных моделей меньшие значения одного из этих критериев указывают на лучшую модель.^[33]
• Стандартная ошибка регрессии это оценка σ, стандартная ошибка члена ошибки.
• Общая сумма квадратов, модельная сумма квадратов, и остаточная сумма квадратов расскажите нам, какая часть первоначального разброса в выборке была объяснена регрессией.
• F-статистика пытается проверить гипотезу о том, что все коэффициенты (кроме точки пересечения) равны нулю. Эта статистика F(p – 1,n – p) распределения при нулевой гипотезе и предположении нормальности, и его p-значение указывает на вероятность того, что гипотеза действительно верна. Обратите внимание, что когда ошибки не являются нормальными, эта статистика становится недействительной, и другие тесты, такие как Тест Вальда или LR тест должен быть использован.

График остатков

Обычный анализ методом наименьших квадратов часто включает использование диагностических графиков, предназначенных для обнаружения отклонений данных от предполагаемой формы модели. Вот некоторые из распространенных диагностических графиков:

• Остатки против независимых переменных в модели. Нелинейная связь между этими переменными предполагает, что линейность функции условного среднего может не выполняться. Различные уровни изменчивости остатков для разных уровней объясняющих переменных предполагают возможную гетероскедастичность.
• Остатки против объясняющих переменных, которых нет в модели. Любая связь остатков с этими переменными предполагает рассмотрение этих переменных для включения в модель.
• Остатки против установленных значений, ${ displaystyle { hat {y}}}$.
• Остатки против предыдущего остатка. Этот график может идентифицировать серийные корреляции в остатках.

Важным моментом при выполнении статистического вывода с использованием регрессионных моделей является выборка данных. В этом примере данные являются средними, а не измерениями по отдельным женщинам. Подгонка модели очень хорошая, но это не означает, что вес отдельной женщины можно предсказать с высокой точностью только на основе ее роста.

Чувствительность к округлению

Этот пример также демонстрирует, что коэффициенты, определяемые этими вычислениями, чувствительны к способу подготовки данных. Первоначально высота была округлена до ближайшего дюйма, а затем преобразована и округлена до ближайшего сантиметра. Поскольку коэффициент преобразования составляет один дюйм на 2,54 см, это не точное преобразование. Исходные дюймы могут быть восстановлены с помощью функции Round (x / 0,0254), а затем преобразованы в метрическую систему без округления. Если это будет сделано, результаты станут:

Остатки до квадратичного соответствия для правильно и неправильно преобразованных данных.

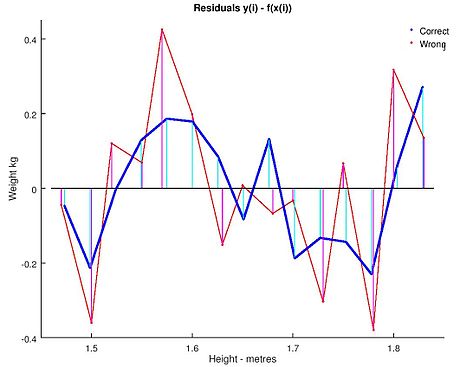
Использование любого из этих уравнений для прогнозирования веса женщины ростом 5 футов 6 дюймов (1,6764 м) дает аналогичные значения: 62,94 кг с округлением по сравнению с 62,98 кг без округления. Таким образом, кажущиеся незначительными отклонения в данных реально влияют на коэффициенты. но небольшое влияние на результаты уравнения.

Хотя это может выглядеть безобидно в середине диапазона данных, оно может стать значимым в крайних случаях или в случае, когда подобранная модель используется для проецирования за пределы диапазона данных (экстраполяция ).

Это подчеркивает общую ошибку: этот пример представляет собой злоупотребление OLS, которое по своей сути требует, чтобы ошибки в независимой переменной (в данном случае высоте) были равны нулю или, по крайней мере, незначительны. Первоначальное округление до ближайшего дюйма плюс любые фактические ошибки измерения составляют конечную ошибку, которой нельзя пренебречь. В результате подобранные параметры не являются наилучшими оценками, как предполагалось. Хотя это и не является полностью ложным, ошибка в оценке будет зависеть от относительного размера Икс и y ошибки.

Другой пример с менее реальными данными

Постановка задачи

Мы можем использовать механизм наименьших квадратов, чтобы выяснить уравнение орбиты двух тел в полярных координатах. Обычно используется уравнение ${ Displaystyle г ( тета) = { гидроразрыва {р} {1-е соз ( тета)}}}$ где ${ Displaystyle г ( тета)}$ - радиус, на котором объект находится от одного из тел. В уравнении параметры ${ displaystyle p}$ и ${ displaystyle e}$ используются для определения траектории орбиты. Мы измерили следующие данные.

${ displaystyle theta}$ (в градусах)	43	45	52	93	108	116
${ Displaystyle г ( тета)}$	4.7126	4.5542	4.0419	2.2187	1.8910	1.7599

Нам нужно найти приближение наименьших квадратов ${ displaystyle e}$ и ${ displaystyle p}$ по приведенным данным.

Решение

Сначала нам нужно представить e и p в линейной форме. Итак, мы собираемся переписать уравнение ${ Displaystyle г ( тета)}$ так как ${ displaystyle { frac {1} {r ( theta)}} = { frac {1} {p}} - { frac {e} {p}} cos ( theta)}$. Теперь мы можем использовать эту форму для представления наших данных наблюдений как:

${ displaystyle A ^ {T} A { binom {x} {y}} = A ^ {T} b}$ где ${ displaystyle x}$ является ${ displaystyle { frac {1} {p}}}$ и ${ displaystyle y}$ является ${ displaystyle { frac {e} {p}}}$ и ${ displaystyle A}$ строится по первому столбцу, являющемуся коэффициентом ${ displaystyle { frac {1} {p}}}$ а второй столбец - коэффициент при ${ displaystyle { frac {e} {p}}}$ и ${ displaystyle b}$ - значения для соответствующих ${ Displaystyle { frac {1} {г ( theta)}}}$ так ${ displaystyle A = { begin {bmatrix} 1 & -0.731354 1 & -0.707107 1 & -0.615661 1 & 0.052336 1 & 0.309017 1 & 0.438371 end {bmatrix}}}$ и ${ displaystyle b = { begin {bmatrix} 0,21220 0,21958 0,24741 0,45071 0,52883 0,56820 end {bmatrix}}.}$

При решении получаем ${ displaystyle { binom {x} {y}} = { binom {0,43478} {0,30435}}}$

так ${ displaystyle p = { frac {1} {x}} = 2,3000}$ и ${ displaystyle e = p cdot y = 0,70001}$

Смотрите также

• Байесовский метод наименьших квадратов
• Регрессия Фамы – Макбета
• Нелинейный метод наименьших квадратов
• Численные методы линейных наименьших квадратов
• Идентификация нелинейной системы

использованная литература

дальнейшее чтение

• Догерти, Кристофер (2002). Введение в эконометрику (2-е изд.). Нью-Йорк: Издательство Оксфордского университета. С. 48–113. ISBN  0-19-877643-8.
• Гуджарати, Дамодар Н.; Портер, Дон С. (2009). Основы эконометики (Пятое изд.). Бостон: Макгроу-Хилл Ирвин. С. 55–96. ISBN  978-0-07-337577-9.
• Хилл, Р. Картер; Гриффитс, Уильям Э .; Лим, Гуай С. (2008). Принципы эконометрики (3-е изд.). Хобокен, Нью-Джерси: Джон Уайли и сыновья. С. 8–47. ISBN  978-0-471-72360-8.
• Вулдридж, Джеффри (2008). «Модель простой регрессии». Вводная эконометрика: современный подход (4-е изд.). Мейсон, Огайо: Обучение Cengage. С. 22–67. ISBN  978-0-324-58162-1.