Контрольный график - Control chart

Эта статья включает в себя список общих Рекомендации, но он остается в основном непроверенным, потому что ему не хватает соответствующих встроенные цитаты. Пожалуйста, помогите улучшать эта статья введение более точные цитаты. (Декабрь 2013) (Узнайте, как и когда удалить этот шаблон сообщения)

Контрольный график
Один из Семь основных инструментов качества
Впервые описано	Уолтер А. Шухарт
Цель	Чтобы определить, должен ли процесс проходить формальную экспертизу на предмет проблем, связанных с качеством

Графики контроля, также известный как Графики Шухарта (после Уолтер А. Шухарт ) или же графики поведения процессов, площадь Статистическое управление процессами инструмент, используемый для определения того, производство или же бизнес-процесс находится в состоянии контроль. Более уместно сказать, что контрольные диаграммы являются графическим устройством для статистического мониторинга процессов (SPM). Традиционные контрольные диаграммы в основном предназначены для мониторинга параметров процесса, когда известна лежащая в основе форма распределения процесса. Однако в 21 веке доступны более продвинутые методы, в которых поток входящих данных можно контролировать даже без каких-либо знаний о распределении базовых процессов. Диаграммы контроля без распространения становятся все более популярными.

Обзор

Если анализ контрольной диаграммы показывает, что процесс в настоящее время находится под контролем (т. Е. Стабилен, с отклонениями только от источников, общих для процесса), то никаких исправлений или изменений в параметрах управления процессом не требуется или не желательно. Кроме того, данные процесса можно использовать для прогнозирования будущих показателей процесса. Если диаграмма показывает, что отслеживаемый процесс не находится под контролем, анализ диаграммы может помочь определить источники отклонений, так как это приведет к снижению производительности процесса.^[1] Процесс, который является стабильным, но работает за пределами желаемых (спецификационных) пределов (например, процент брака может находиться под статистическим контролем, но выше желаемых пределов), должен быть улучшен за счет целенаправленных усилий, направленных на понимание причин текущей производительности и фундаментального улучшения процесса.^[2]

Контрольная диаграмма является одним из семь основных инструментов из контроль качества.^[3] Обычно контрольные диаграммы используются для данных временных рядов, хотя их можно использовать для данных, которые имеют логическую сопоставимость (т. Е. Вы хотите сравнить образцы, которые были взяты все одновременно, или показатели разных людей); однако тип диаграммы, используемой для этого, требует рассмотрения.^[4]

История

Контрольная карта была изобретена Уолтер А. Шухарт работая на Bell Labs в 1920-е гг.^[5] Инженеры компании стремились повысить надежность своих телефония системы передачи. Потому что усилители и другое оборудование пришлось закопать под землю, возникла более серьезная потребность бизнеса в сокращении частоты отказов и ремонтов. К 1920 году инженеры уже осознали важность уменьшения вариаций в производственном процессе. Более того, они осознали, что постоянная корректировка процесса в ответ на несоответствие фактически увеличивает вариативность и снижает качество. Шухарт сформулировал проблему с точки зрения Общие и особые причины изменений и 16 мая 1924 г. написал служебную записку, в которой представил контрольную диаграмму как инструмент для различия между ними. Босс Шухарта, Джордж Эдвардс, вспоминал: «Доктор Шухарт подготовил небольшой меморандум размером всего около страницы. Около трети этой страницы было отведено под простую диаграмму, которую мы все сегодня узнали бы как схематическую контрольную диаграмму. Эта диаграмма , и краткий текст, который предшествовал ему и последовал за ним, излагал все основные принципы и соображения, которые используются в том, что мы сегодня знаем как контроль качества процесса ».^[6] Шухарт подчеркнул, что приведение производственного процесса в состояние статистический контроль, где есть только Общая причина вариации и контроль над ними необходимы для прогнозирования будущих результатов и для экономичного управления процессом.

Шухарт создал основу для контрольной диаграммы и концепции состояния статистического контроля с помощью тщательно разработанных экспериментов. Хотя Шухарт опирался на чисто математические статистические теории, он понимал, что данные физических процессов обычно производят "нормальное распределение кривая "(a Гауссово распределение, также обычно называемый "кривая колокола Он обнаружил, что наблюдаемые различия в производственных данных не всегда ведут себя так же, как данные в природе (Броуновское движение частиц). Шухарт пришел к выводу, что, хотя каждый процесс демонстрирует вариации, некоторые процессы демонстрируют контролируемые вариации, которые естественны для процесса, в то время как другие демонстрируют неконтролируемые вариации, которые не присутствуют в причинной системе процесса все время.^[7]

В 1924 или 1925 году нововведение Шухарта привлекло внимание У. Эдвардс Деминг, а затем работая в Хоторнский объект. Позже Деминг работал в Министерство сельского хозяйства США и стал математическим советником Бюро переписи населения США. В течение следующих полувека Деминг стал главным поборником и сторонником работы Шухарта. После поражения Япония в конце Вторая Мировая Война, Деминг работал статистическим консультантом Верховный главнокомандующий союзных держав. Его последующее участие в японской жизни и долгая карьера в качестве промышленного консультанта распространили мышление Шухарта и использование контрольной диаграммы в японской обрабатывающей промышленности на протяжении 1950-х и 1960-х годов.

Детали диаграммы

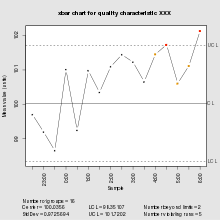
Контрольный график состоит из:

• Точки, представляющие статистику (например, иметь в виду, диапазон, пропорция) измерений характеристики качества в образцах, взятых в процессе в разное время (т. е. данные)
• Вычисляется среднее значение этой статистики с использованием всех выборок (например, среднее значение средних значений, среднее значение диапазонов, среднее значение пропорций).
• Центральная линия проведена на уровне среднего значения статистики.
• В стандартное отклонение (например, sqrt (дисперсия) среднего) статистики также вычисляется с использованием всех выборок.
• Верхний и нижний контрольные пределы (иногда называемые «естественными пределами процесса»), которые указывают пороговое значение, при котором результаты процесса считаются статистически «маловероятными» и обычно отображаются при трех стандартных отклонениях от центральной линии.

Диаграмма может иметь другие дополнительные функции, в том числе:

• Верхний и нижний предупредительные или контрольные пределы, нарисованные отдельными линиями, обычно на два стандартных отклонения выше и ниже центральной линии
• Разделение на зоны с добавлением правил, регулирующих периодичность наблюдений в каждой зоне
• Аннотация с интересующими событиями, определенными инженером по качеству, отвечающим за качество процесса
• Действия по особым причинам

(n.b., существует несколько наборов правил для обнаружения сигнала; это только один набор. Набор правил должен быть четко сформулирован.)

1. Любая точка за пределами контроля
2. Пробежка из 7 точек над или под центральной линией - остановка производства
   • Карантин и 100% проверка
   • Отрегулируйте процесс.
   • Проверить 5 последовательных проб
   • Продолжить процесс.
3. Прогон на 7 пунктов вверх или вниз - инструкция, как указано выше

Использование диаграммы

Если процесс находится под контролем (и статистика процесса нормальная), 99,7300% всех точек будут находиться между контрольными пределами. Любые наблюдения, выходящие за пределы, или систематические закономерности в пределах, предполагают введение нового (и, вероятно, непредвиденного) источника вариаций, известного как особая причина вариация. Поскольку увеличение вариации означает увеличение затраты на качество, контрольная диаграмма, «сигнализирующая» о наличии особой причины, требует немедленного исследования.

Это делает контрольные пределы очень важными помощниками при принятии решений. Контрольные пределы предоставляют информацию о поведении процесса и не имеют внутреннего отношения к каким-либо Технические характеристики цели или инженерная терпимость. На практике среднее значение процесса (и, следовательно, центральная линия) может не совпадать с заданным значением (или целевым показателем) характеристики качества, потому что разработка процесса просто не может предоставить характеристику процесса на желаемом уровне.

Лимит контрольных графиков пределы спецификации или целей из-за тенденции тех, кто вовлечен в процесс (например, операторов машин), сосредоточиться на выполнении в соответствии со спецификацией, тогда как на самом деле наименее затратный курс действий состоит в том, чтобы поддерживать как можно более низкие вариации процесса. Попытка заставить процесс, естественный центр которого не совпадает с целевым, работать в соответствии с целевой спецификацией, увеличивает изменчивость процесса и значительно увеличивает затраты и является причиной значительной неэффективности операций. Возможности процесса Однако исследования действительно исследуют взаимосвязь между естественными пределами процесса (контрольные пределы) и спецификациями.

Назначение контрольных диаграмм - обеспечить простое обнаружение событий, указывающих на фактическое изменение процесса. Это простое решение может оказаться трудным, если характеристики процесса постоянно меняются; на контрольной карте представлены статистически объективные критерии изменения. Когда изменение обнаруживается и считается хорошим, его причина должна быть идентифицирована и, возможно, стать новым способом работы, а если изменение плохое, то его причина должна быть выявлена ​​и устранена.

Целью добавления пределов предупреждений или разделения контрольной диаграммы на зоны является своевременное уведомление, если что-то не так. Вместо того, чтобы немедленно начать работу по улучшению процесса, чтобы определить, присутствуют ли особые причины, инженер по качеству может временно увеличить скорость, с которой берутся образцы из выходных данных процесса, пока не станет ясно, что процесс действительно находится под контролем. Обратите внимание, что с пределами трех сигм, Общая причина вариации приводят к сигналам менее одного раза из каждых двадцати двух точек для искаженных процессов и примерно один раз из каждых трехсот семидесяти (1 / 370,4) точек для нормально распределенных процессов.^[8] Уровни предупреждения о двух сигмах будут достигнуты примерно один раз для каждых двадцати двух (1 / 21,98) точек на графике в нормально распределенных данных. (Например, в соответствии с Центральной предельной теоремой средние значения достаточно больших выборок, взятых практически из любого базового распределения, имеющего дисперсию, распределены нормально.)

Выбор лимитов

Набор Шухарта 3-сигма (3-стандартное отклонение) пределы на следующей основе.

• Грубый результат Неравенство Чебышева что для любого распределение вероятностей, то вероятность результата больше, чем k Стандартное отклонение от иметь в виду не больше 1 /k².
• Лучший результат Неравенство Высочанского – Петунина., что для любого унимодальное распределение вероятностей, то вероятность результата больше, чем k Стандартное отклонение от иметь в виду не больше 4 / (9k²).
• в Нормальное распределение, очень распространенный распределение вероятностей, 99,7% наблюдений происходят в пределах трех Стандартное отклонение из иметь в виду (видеть Нормальное распределение ).

Шухарт резюмировал выводы, сказав:

... тот факт, что критерий, который мы используем, имеет прекрасное происхождение от интеллектуальных статистических теорем, не оправдывает его использования. Такое обоснование должно исходить из эмпирических доказательств того, что это работает. Как сказал бы инженер-практик, доказательство пудинга заключается в его поедании.^[9]

Хотя изначально он экспериментировал с ограничениями, основанными на распределения вероятностей, В конце концов Шухарт написал:

Некоторые из самых ранних попыток охарактеризовать состояние статистического контроля были вдохновлены убеждением, что существует особая форма частотной функции. ж и рано утверждалось, что нормальный закон характеризует такое состояние. Когда нормальный закон был признан неадекватным, были опробованы обобщенные функциональные формы. Однако сегодня все надежды на поиск уникальной функциональной формы ж взорваны.^{[нужна цитата ]}

Контрольная диаграмма предназначена для эвристический. Деминг настаивал на том, что это не проверка гипотез и не мотивирован Лемма Неймана – Пирсона.. Он утверждал, что непересекающийся характер численность населения и основа выборки в большинстве промышленных ситуаций ставится под угрозу использование обычных статистических методов. Деминг намерение состояло в том, чтобы получить представление о система причин процесса ... в широком диапазоне неизвестных обстоятельств, будущих и прошлых ....^{[нужна цитата ]} Он утверждал, что в таких условиях 3-сигма предоставленные ограничения ... рациональное и экономичное руководство к минимуму экономических потерь ... из двух ошибок:^{[нужна цитата ]}

1. Отнесите вариацию или ошибку к особой причине (приписываемая причина), когда на самом деле причина принадлежит системе (общая причина). (Также известен как Ошибка типа I или ложноположительный)
2. Приписать системе вариацию или ошибку (общие причины), когда на самом деле причиной была особая причина (назначаемая причина). (Также известен как Ошибка типа II или ложноотрицательный)

Расчет стандартного отклонения

Что касается расчета контрольных пределов, то стандартное отклонение (ошибка) требуется - это ошибка Общая причина вариации в процессе. Следовательно, обычный оценщик, в терминах дисперсии выборки, не используется, поскольку это оценивает общую потерю квадратичной ошибки от обоих общие и особые причины вариации.

Альтернативный метод - использовать связь между классифицировать образца и его стандартное отклонение полученный Леонард Х. К. Типпетт, как оценщик, на который, как правило, меньше влияют экстремальные наблюдения, типичные для особые причины.^{[нужна цитата ]}

Правила обнаружения сигналов

Самые распространенные наборы:

• В Правила Western Electric
• В Уиллер правила (эквивалент зональных тестов Western Electric^[10])
• В Правила Нельсона

Были особые разногласия относительно того, как долго серия наблюдений, все на одной стороне от центральной линии, должна считаться сигналом, причем 6, 7, 8 и 9 все поддерживаются различными авторами.

Самый важный принцип выбора набора правил - выбор должен быть сделан до проверки данных. Выбор правил после того, как данные были просмотрены, как правило, увеличивает Ошибка типа I ставка из-за эффекты тестирования, предложенные данными.

Альтернативные базы

В 1935 г. Британский институт стандартов, под влиянием Эгон Пирсон и вопреки духу Шухарта принял контрольные карты, заменив 3-сигма лимиты с лимитами на основе процентили из нормальное распределение. Этот ход по-прежнему представлен Джон Окленд и другие, но широко осуждался писателями традиции Шухарта-Деминга.

Выполнение контрольных карт

Когда точка выходит за пределы, установленные для данной контрольной карты, ожидается, что лица, ответственные за базовый процесс, определят, возникла ли особая причина. Если да, то уместно определить, лучше или хуже результаты по особой причине, чем результаты только по общим причинам. В худшем случае эту причину следует по возможности устранить. Если лучше, может быть целесообразно намеренно сохранить особую причину в системе, дающей результаты.^{[нужна цитата ]}

Даже когда процесс под контролем (то есть, в системе отсутствуют какие-либо особые причины), существует приблизительно 0,27% вероятность того, что точка превысит 3-сигма контрольные пределы. Таким образом, даже контролируемый процесс, нанесенный на правильно построенную контрольную диаграмму, в конечном итоге сигнализирует о возможном наличии особой причины, даже если она на самом деле могла не возникнуть. Для контрольной диаграммы Шухарта с использованием 3-сигма пределы, это ложная тревога происходит в среднем один раз каждые 1 / 0,0027 или 370,4 наблюдения. Следовательно контролируемая средняя длина пробега (или контролируемый ARL) диаграммы Шухарта составляет 370,4.^{[нужна цитата ]}

Между тем, если возникает особая причина, она может оказаться недостаточной для того, чтобы диаграмма произвела немедленное состояние тревоги. Если возникает особая причина, ее можно описать, измерив изменение среднего значения и / или дисперсии рассматриваемого процесса. Когда эти изменения количественно определены, можно определить неконтролируемый ARL для диаграммы.^{[нужна цитата ]}

Оказывается, диаграммы Шухарта достаточно хороши для обнаружения больших изменений в среднем или дисперсии процесса, поскольку их неконтролируемые ARL в этих случаях довольно короткие. Однако для небольших изменений (например, 1- или же 2-сигма изменение среднего), диаграмма Шухарта не обнаруживает эти изменения эффективно. Были разработаны другие типы контрольных карт, такие как График EWMA, то CUSUM диаграмму и диаграмму контрастов в реальном времени, которые более эффективно обнаруживают более мелкие изменения за счет использования информации из наблюдений, собранных до самой последней точки данных.^[11]

Многие контрольные диаграммы лучше всего подходят для числовых данных с предположениями Гаусса. Диаграмма контрастов в реальном времени была предложена для мониторинга процессов со сложными характеристиками, например многомерные, смешанные числовые и категориальные, с пропущенными значениями, негауссовские, нелинейные отношения.^[11]

Критика

Некоторые авторы критиковали контрольную диаграмму на том основании, что она нарушает принцип правдоподобия.^{[нужна цитата ]} Однако сам по себе принцип является спорным, и сторонники контрольных карт далее утверждают, что в целом невозможно указать функция правдоподобия для процесса, не подлежащего статистическому контролю, особенно когда знание система причин процесса слабый.^{[нужна цитата ]}

Некоторые авторы критиковали использование средней длины прогона (ARL) для сравнения производительности контрольной диаграммы, потому что это среднее обычно следует за геометрическое распределение, имеющий высокую вариабельность и сложность.^{[нужна цитата ]}

Некоторые авторы критиковали, что большинство контрольных диаграмм сосредоточено на числовых данных. В настоящее время данные процесса могут быть намного более сложными, например негауссовские, смешанные числовые и категориальные или с пропущенными значениями.^[11]

Типы графиков

Диаграмма	Наблюдение за процессом	Отношения между наблюдениями за процессом	Тип наблюдения за процессом	Размер сдвига для обнаружения
${ displaystyle { bar {x}}}$ и R диаграмма	Измерение качественных характеристик в пределах одной подгруппы	Независимый	Переменные	Большой (≥ 1,5σ)
${ displaystyle { bar {x}}}$ и s диаграмма	Измерение качественных характеристик внутри одной подгруппы	Независимый	Переменные	Большой (≥ 1,5σ)
Контрольная карта индивидуумов Шухарта (Диаграмма ImR или диаграмма XmR)	Измерение качественных характеристик за одно наблюдение	Независимый	Переменные†	Большой (≥ 1,5σ)
Трехсторонняя диаграмма	Измерение качественных характеристик в пределах одной подгруппы	Независимый	Переменные	Большой (≥ 1,5σ)
p-диаграмма	Доля несоответствующих внутри одной подгруппы	Независимый	Атрибуты†	Большой (≥ 1,5σ)
np-диаграмма	Количество несоответствующих внутри одной подгруппы	Независимый	Атрибуты†	Большой (≥ 1,5σ)
c-диаграмма	Количество несоответствий в одной подгруппе	Независимый	Атрибуты†	Большой (≥ 1,5σ)
u-диаграмма	Несоответствий на единицу внутри одной подгруппы	Независимый	Атрибуты†	Большой (≥ 1,5σ)
График EWMA	Экспоненциально взвешенное скользящее среднее измерения качественных характеристик в рамках одной подгруппы	Независимый	Атрибуты или переменные	Маленький (<1,5σ)
CUSUM Диаграмма	Кумулятивная сумма измерений характеристик качества внутри одной подгруппы	Независимый	Атрибуты или переменные	Маленький (<1,5σ)
Временные ряды модель	Измерение качественных характеристик внутри одной подгруппы	Автокоррелированный	Атрибуты или переменные	Нет данных
График контроля регрессии	Измерение качественных характеристик в пределах одной подгруппы	Зависит от переменных управления процессом	Переменные	Большой (≥ 1,5σ)

^†Некоторые практики также рекомендуют использовать индивидуальные диаграммы для атрибутивных данных, особенно когда нарушаются предположения либо о биномиально распределенных данных (p- и np-диаграммы), либо о данных с распределением Пуассона (u- и c-диаграммы).^[12] Даются два основных обоснования этой практики. Во-первых, нормальность не требуется для статистического контроля, поэтому диаграмму отдельных лиц можно использовать с ненормальными данными.^[13] Во-вторых, диаграммы атрибутов получают меру дисперсии непосредственно из средней доли (путем допущения распределения вероятностей), в то время как диаграммы отдельных лиц получают меру дисперсии из данных, независимо от среднего, что делает диаграммы отдельных лиц более надежными, чем диаграммы атрибутов, для нарушений предположения о распределении основной популяции.^[14] Иногда отмечают, что подстановка индивидуальной диаграммы лучше всего работает для больших подсчетов, когда биномиальная и Распределения Пуассона приблизиться к нормальному распределению. т.е. когда количество испытаний п > 1000 для p- и np-диаграмм или λ > 500 для u- и c-графиков.

Критики этого подхода утверждают, что контрольные диаграммы не следует использовать, когда нарушаются лежащие в их основе предположения, например, когда данные процесса не распределены ни нормально, ни биномиально (или по Пуассону). Такие процессы неконтролируемы и должны быть улучшены перед применением контрольных карт. Кроме того, применение графиков при таких отклонениях увеличивает ошибка типа I и типа II скорости контрольных карт, и эта диаграмма может иметь мало практического применения.^{[нужна цитата ]}

Смотрите также

• Аналитические и перечислительные статистические исследования
• Общая причина и особая причина
• График контроля без распространения
• У. Эдвардс Деминг
• Возможности процесса
• Семь основных инструментов качества
• Шесть Сигм
• Статистическое управление процессами
• Полное управление качеством

Рекомендации

Библиография

• Деминг, В. Э. (1975). «О вероятности как основании действия». Американский статистик. 29 (4): 146–152. CiteSeerX  10.1.1.470.9636. Дои:10.2307/2683482. JSTOR  2683482.
• Деминг, В. Э. (1982). Выход из кризиса: качество, производительность и конкурентоспособность. ISBN  978-0-521-30553-2.
• Deng, H .; Runger, G .; Тув, Евгений (2012). «Системный мониторинг с контрастами в реальном времени». Журнал качественных технологий. 44 (1): 9–27. Дои:10.1080/00224065.2012.11917878.
• Мандель, Б. Дж. (1969). «График контроля регрессии». Журнал качественных технологий. 1 (1): 1–9. Дои:10.1080/00224065.1969.11980341.
• Окленд, Дж. (2002). Статистическое управление процессами. ISBN  978-0-7506-5766-2.
• Шухарт, В. А. (1931). Экономический контроль качества выпускаемой продукции. ISBN  978-0-87389-076-2.
• Шухарт, В. А. (1939). Статистический метод с точки зрения контроля качества. ISBN  978-0-486-65232-0.
• Уиллер, Д. Дж. (2000). Нормальность и диаграмма процесс-поведение. ISBN  978-0-945320-56-2.
• Уиллер, Д. Дж .; Чемберс, Д. С. (1992). Понимание статистического управления процессами. ISBN  978-0-945320-13-5.
• Уилер, Дональд Дж. (1999). Понимание вариативности: ключ к управлению хаосом (2-е изд.). SPC Press. ISBN  978-0-945320-53-1.

внешняя ссылка

• Электронный справочник статистических методов NIST / SEMATECH
• Мониторинг и контроль с помощью контрольных диаграмм