Правила Нельсона - Nelson rules
Правила Нельсона метод в контроль над процессом определения того, выходит ли какая-либо измеряемая переменная из-под контроля (непредсказуемая или непротиворечивая). Правила для обнаружения "неконтролируемых" или неслучайных условий были впервые постулированы Уолтер А. Шухарт [1] в 1920-е гг. Правила Нельсона были впервые опубликованы в октябрьском выпуске 1984 г. Журнал качественных технологий в статье Ллойд С. Нельсон.[2]
Правила применяются к контрольная диаграмма на котором величина некоторых Переменная построен против времени. Правила основаны на иметь в виду ценность и стандартное отклонение образцов.
| Правило | Описание | Пример диаграммы | Указанная проблема |
|---|---|---|---|
| Один балл составляет более 3 стандартных отклонений от среднего. |  | Один образец (в данном случае показаны два) явно выходит из-под контроля. | |
| Девять (или более) точек подряд находятся по одну сторону от среднего. | 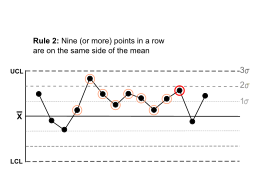 | Некоторые продолжительные предвзятость существуют. | |
| Шесть (или более) очков подряд постоянно увеличиваются (или уменьшаются). | 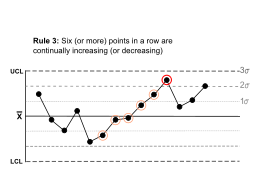 | А тенденция существуют. | |
| Четырнадцать (или более) точек подряд чередуются по направлению, увеличиваясь и уменьшаясь. | 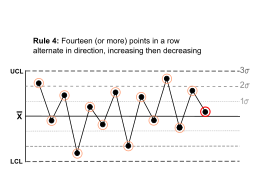 | Этого достаточно колебание вне шум. Обратите внимание, что правило касается только направленности. Положение среднего значения и величина стандартного отклонения не имеют значения. | |
| Две (или три) из трех точек подряд имеют более 2 стандартных отклонений от среднего в одном и том же направлении. |  | Существует средняя тенденция к выходу образцов из-под контроля. Сторона среднего для третьей точки не указана. | |
| Четыре (или пять) из пяти точек подряд имеют более чем 1 стандартное отклонение от среднего в том же направлении. | 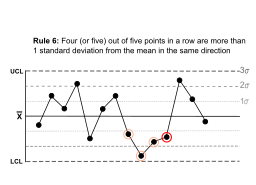 | Существует сильная тенденция к тому, что образцы немного выходят из-под контроля. Сторона среднего для пятой точки не указана. | |
| Пятнадцать точек подряд находятся в пределах 1 стандартного отклонения от среднего по обе стороны от среднего. |  | При 1 стандартном отклонении можно ожидать большего разброса. | |
| Существуют восемь точек подряд, но ни одна из них не находится в пределах 1 стандартного отклонения от среднего, и точки находятся в обоих направлениях от среднего. | 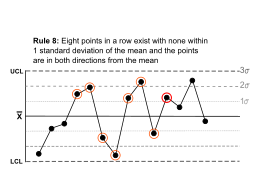 | Переход сверху вниз при отсутствии первой полосы стандартного отклонения редко бывает случайным. |
Вышеупомянутые восемь правил применимы к диаграмме значения переменной.
Второй график, движущийся классифицировать диаграмму, также можно использовать, но только с правилами 1, 2, 3 и 4. Такая диаграмма строит график максимального значения - минимального значения N соседние точки относительно временной выборки диапазона.
Пример диапазона перемещения: если N = 3 и значения равны 1, 3, 5, 3, 3, 2, 4, 5, то наборы соседних точек равны (1,3,5) (3,5,3) (5 , 3,3) (3,3,2) (3,2,4) (2,4,5), в результате чего значения диапазона перемещения (5-1) (5-3) (5-3) (3- 2) (4-2) (5-2) = 4, 2, 2, 1, 2, 3.
Применение этих правил указывает на возникновение потенциальной ситуации «выхода из-под контроля». Однако всегда будут ложные срабатывания, и чем больше правил будет применяться, тем больше будет случаев. Для некоторых процессов может быть полезно опустить одно или несколько правил. Точно так же могут отсутствовать некоторые предупреждения, когда не обнаруживается какая-то конкретная «неконтролируемая» ситуация. Опытным путем обнаружение точность хороший.
Смотрите также
- Общая причина и особая причина
- Статистическое управление процессами
- Правила Western Electric
- Правила Вестгарда
- Американское общество качества, Инструменты качества
Рекомендации
- ^ Справочник по инженерной статистике 6.3.2, Электронный справочник статистических методов NIST / SEMATECH Национальный институт стандартов и технологий, Декабрь 2006 г.
- ^ Ллойд С. Нельсон, "Контрольная карта Шухарта - тесты для особых причин". Журнал технологий качества 16, вып. 4 (октябрь 1984 г.), 238-239. https://doi.org/10.1080/00224065.1984.11978921
