График Дика - Dyck graph
| График Дика | |
|---|---|
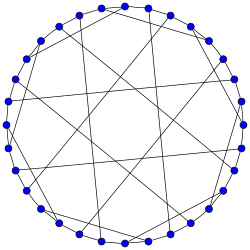 График Дика | |
| Названный в честь | В. Дайк |
| Вершины | 32 |
| Края | 48 |
| Радиус | 5 |
| Диаметр | 5 |
| Обхват | 6 |
| Автоморфизмы | 192 |
| Хроматическое число | 2 |
| Хроматический индекс | 3 |
| Толщина книги | 3 |
| Номер очереди | 2 |
| Характеристики | Симметричный Кубический Гамильтониан Двудольный Граф Кэли |
| Таблица графиков и параметров | |
в математический поле теория графов, то График Дика это 3-регулярный график с 32 вершинами и 48 ребрами, названные в честь Вальтер фон Дейк.[1][2]
это Гамильтониан со 120 различными гамильтоновыми циклами. Она имеет хроматическое число 2, хроматический индекс 3, радиус 5, диаметр 5 и обхват 6. Это также 3-вершинно-связанный и 3-реберный график. Она имеет толщина книги 3 и номер очереди 2.[3]
Граф Дика - это тороидальный граф, а двойственным к его симметричному тороидальному вложению является Граф Шриханде, сильно регулярный граф как симметричный, так и гамильтонов.
Алгебраические свойства
Группа автоморфизмов графа Дика - это группа порядка 192.[4] Он действует транзитивно на вершинах, на ребрах и на дугах графа. Следовательно, граф Дика является симметричный граф. У него есть автоморфизмы, которые переводят любую вершину в любую другую вершину и любое ребро в любое другое ребро. Согласно Приемная перепись, граф Дика, обозначаемый как F32A, является единственным кубическим симметричным графом с 32 вершинами.[5]
В характеристический многочлен графа Дика равно .
Карта Дика
Граф Дика - это скелет из симметричная тесселяция поверхности род три на двенадцать восьмиугольников, известных как Карта Дика или же Дайк черепица. В двойственный граф для этой плитки полный трехсторонний граф K4,4,4.[6][7]
Галерея

Альтернативный рисунок графа Дика.

В хроматическое число графа Дика равно 2.

В хроматический индекс графа Дика равно 3.
Рекомендации
- ^ Дайк, В. (1881), "Über Aufstellung und Untersuchung von Gruppe und Irrationalität Regärer Riemann'scher Flächen", Математика. Анна., 17: 473, Дои:10.1007 / bf01446929.
- ^ Вайсштейн, Эрик В. "График Дайка". MathWorld.
- ^ Вольц, Джессика; Инженерные линейные схемы с SAT. Магистерская работа, Тюбингенский университет, 2018 г.
- ^ Ройл, Г. F032A данные[постоянная мертвая ссылка ]
- ^ Кондер, М.; Добчаньи, П. (2002), "Трехвалентные симметрические графы до 768 вершин", J. Combin. Математика. Комбинировать. Comput., 40: 41–63.
- ^ Дайк, В. (1880), "Notiz über eine Regäre Riemannsche Fläche vom Geschlecht 3 und die zugehörige Normalkurve 4. Ordnung", Математика. Анна., 17: 510–516, Дои:10.1007 / bf01446930.
- ^ Ceulemans, A. (2004), "Тетракизоктаэдрическая группа графа Дика и ее молекулярная реализация.", Молекулярная физика, 102 (11): 1149–1163, Дои:10.1080/00268970410001728780.




