Регулярная карта (теория графов) - Regular map (graph theory)

Гексагональный осоэдр, правильная карта на сфере с двумя вершинами, шестью ребрами, шестью гранями и 24 флагами.

В математика, а обычная карта симметричный мозаика закрытого поверхность. Точнее, регулярное отображение - это разложение двумерного многообразие (например, сфера, тор, или реальная проективная плоскость ) на топологические диски такие, что каждый флаг (инцидентная тройка вершина-ребро-грань) может быть преобразована в любой другой флаг с помощью симметрия разложения. Регулярные отображения в некотором смысле являются топологическими обобщениями Платоновы тела. Теория карт и их классификация связана с теорией Римановы поверхности, гиперболическая геометрия, и Теория Галуа. Обычные карты классифицируются по: род и ориентируемость опорной поверхности, нижележащий граф, или группа автоморфизмов.

Обзор

Регулярные отображения обычно определяются и изучаются тремя способами: топологически, теоретико-групповым и теоретико-графическим.

Топологический подход

Топологически карта - это 2-элементный разложение замкнутого компактного 2-многообразия.

Род gi отображения M задается формулой Отношение Эйлера ${displaystyle chi (M) = | V | - | E | + | F |}$ что равно ${displaystyle 2-2g}$ если карта ориентируемая, и ${displaystyle 2-g}$ если карта неориентируемая. Ключевым фактом является то, что существует конечное (ненулевое) число регулярных отображений для каждого ориентируемого рода, кроме тора.

Теоретико-групповой подход

Теоретически групповое представление перестановки регулярного отображения M переходный группа перестановок C, на съемочной площадке ${displaystyle Omega}$ из флаги, порожденная тремя инволюциями без неподвижной точки р₀, р₁, р₂ удовлетворение (г₀р₂)²= I. В этом определении грани являются орбитами F = <р₀, р₁>, ребра - орбиты E = <р₀, р₂>, а вершины - орбиты V = <р₁, р₂>. Более абстрактно, группа автоморфизмов любого регулярного отображения - это невырожденный гомоморфный образ a <2, m, n> -группа треугольников.

Теоретико-графический подход

Теоретически графическая карта - это кубический граф ${displaystyle Gamma}$ с краями, окрашенными в синий, желтый, красный цвет, такие, что: ${displaystyle Gamma}$ связно, каждая вершина инцидентна одному ребру каждого цвета, а циклы ребер, не окрашенных в желтый цвет, имеют длину 4. Обратите внимание, что ${displaystyle Gamma}$ это граф флагов или карта с графическим кодированием (GEM) карты, определенной на вершине множества флагов ${displaystyle Omega}$ и не является каркасом G = (V, E) карты. В общем, | ${displaystyle Omega}$ | = 4 | E |.

Отображение M правильно тогда и только тогда, когда Aut (M) действует регулярно на флагах. Aut (M) регулярного отображения транзитивно на вершинах, ребрах и граняхM. Карта M называется рефгибким тогда и только тогда, когда Aut (M) регулярна и содержит автоморфизм ${displaystyle phi}$ который фиксирует как вершинуv и лицож, но меняет порядок ребер. Карта, которая является правильной, но негибкой, называется хиральный.

Примеры

Полукуб, обычная карта.

В большой додекаэдр - правильное отображение с пятиугольными гранями на ориентируемой поверхности рода 4.
В гемикуб является регулярным отображением типа {4,3} в проективная плоскость.
В полудодекаэдр является правильным отображением, полученным пятиугольным вложением графа Петерсена в проективную плоскость.
П-осоэдр является регулярным отображением типа {2, p}.
В Карта Дика - правильная карта из 12 восьмиугольников на поверхности рода 3. Его базовый график, График Дика, также может образовывать правильное отображение 16 шестиугольников в торе.

Ниже приводится полный список регулярных отображений на поверхностях положительного Эйлерова характеристика, χ: сфера и проективная плоскость.^[1]

χ	г	Schläfli	Vert.	Края	Лица	Группа	порядок	График	Заметки
2	0	{p, 2}	п	п	2	C₂ × Dih_п	4п	C_п	Дигедрон
2	0	{2, п}	2	п	п	C₂ × Ди_п	4п	п-сложить K₂	Хосоэдр
2	0	{3,3}	4	6	4	S₄	24	K₄	Тетраэдр
2	0	{4,3}	8	12	6	C₂ × S₄	48	K₄ × K₂	Куб
2	0	{3,4}	6	12	8	C₂ × S₄	48	K_2,2,2	Октаэдр
2	0	{5,3}	20	30	12	C₂ × А₅	120		Додекаэдр
2	0	{3,5}	12	30	20	C₂ × А₅	120	K₆ × K₂	Икосаэдр
1	n1	{2п, 2} / 2	п	п	1	Dih_2п	4п	C_п	Полудиэдр^[2]
1	n1	{2,2p} / 2	2	п	п	Dih_2п	4п	п-сложить K₂	Полусоэдр^[2]
1	n1	{4,3}/2	4	6	3	S₄	24	K₄	Hemicube
1	n1	{3,4}/2	3	6	4	S₄	24	2-кратный K₃	Гемиоктаэдр
1	n1	{5,3}/2	10	15	6	А₅	60	Граф Петерсена	Гемидодекаэдр
1	n1	{3,5}/2	6	15	10	А₅	60	K₆	Полуикосаэдр

На изображениях ниже показаны три из 20 обычных карт в тройной тор, помеченные своими Символы Шлефли.

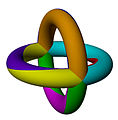
{6,4}
{4,8}
{8,4}

Тороидальные многогранники

Пример в виде сетей
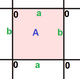{4,4}_1,0 (v: 1, e: 2, f: 1)	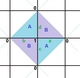{4,4}_1,1 (v: 2, e: 4, f: 2)	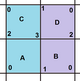{4,4}_2,0 (v: 4, e: 8, f: 4)	{4,4}_2,1 (v: 5, e: 10, f: 5)	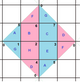{4,4}_2,2 (v: 8, e: 16, f: 8)
{3,6}_1,0 (v: 1, e: 3, f: 2)	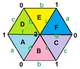{3,6}_1,1 (v: 3, e: 9, f: 6)	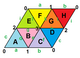{3,6}_2,0 (v: 4, e: 8, f: 8)	{3,6}_2,1 (v: 7, e: 21, f: 14)	{3,6}_2,2 (v: 12, e: 36, f: 24)
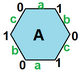{6,3}_1,0 (v: 2, e: 3, f: 1)	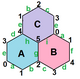{6,3}_1,1 (v: 6, e: 9, f: 3)	{6,3}_2,0 (v: 8, e: 8, f: 4)	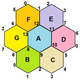{6,3}_2,1 (v: 14, e: 21, f: 7)	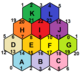{6,3}_2,2 (v: 24, e: 36, f: 12)

Регулярные отображения существуют как тороэдрические многогранники как конечные части евклидовых мозаик, намотанные на поверхность дуоцилиндр как плоский тор. Они помечены {4,4}_б,c для тех, кто связан с квадратная черепица, {4,4}.^[3] {3,6}_б,c связаны с треугольная черепица, {3,6} и {6,3}_б,c связанный с шестиугольная черепица, {6,3}. б и c находятся целые числа.^[4] Есть 2 особых случая (б, 0) и (б,б) с отражательной симметрией, а общие случаи существуют в киральных парах (б,c) и (c,б).

Регулярные карты вида {4,4}_м,0 можно представить как конечное правильный косой многогранник {4,4 | м}, видимые как квадратные грани м×м дуопризма в 4-х измерениях.

Вот пример {4,4}_8,0 нанесен на карту с самолета как шахматная доска сечению цилиндра к тору. Проекция из цилиндра на тор искажает геометрию в трех измерениях, но может быть выполнена без искажений в четырех измерениях.

Например, карта {6,4}₃ можно увидеть как {6,4}_4,0. Следуя противоположным краям, мы последовательно пересечем все 4 шестиугольника.

Обычные карты с нулем Эйлерова характеристика^[5]
г	Schläfli	Vert.	Края	Лица	Группа	порядок	Заметки
1	{4,4}_б,0 п=б²	п	2п	п	[4,4]_(б,0)	8п	Плоские тороидальные многогранники То же, что и {4,4 \| б}
1	{4,4}_б,б п=2б²	п	2п	п	[4,4]_(б,б)	8п	Плоские тороидальные многогранники То же, что и ректификованный {4,4 \| б}
1	{4,4}_б,c п=б²+c²	п	2п	п	[4,4]⁺ _{_(б,c)}	4п	Плоские киральные тороидальные многогранники
1	{3,6}_б,0 т=б²	т	3т	2т	[3,6]_(б,0)	12т	Плоские тороидальные многогранники
1	{3,6}_б,б т=2б²	т	3т	2т	[3,6]_(б,б)	12т	Плоские тороидальные многогранники
1	{3,6}_б,c т=б²+до н.э+c²	т	3т	2т	[3,6]⁺ _{_(б,c)}	6т	Плоские киральные тороидальные многогранники
1	{6,3}_б,0 т=б²	2т	3т	т	[3,6]_(б,0)	12т	Плоские тороидальные многогранники
1	{6,3}_б,б т=2б²	2т	3т	т	[3,6]_(б,б)	12т	Плоские тороидальные многогранники
1	{6,3}_б,c т=б²+до н.э+c²	2т	3т	т	[3,6]⁺ _{_(б,c)}	6т	Плоские киральные тороидальные многогранники

В общих правильных тороидальных многогранниках {п,q}_б,c можно определить, если п или q четные, хотя только вышеперечисленные евклидовы могут существовать как тороидальные многогранники в четырех измерениях. В {2п,q} пути (б,c) можно определить как ступенчатую грань-кромку-грань по прямым линиям, а двойственный {п,2q} формы будут видеть пути (б,c) как шагающая вершина-ребро-вершина по прямым линиям.

Смотрите также

использованная литература

^ Кокстер (1980)
^ ^а ^б Секин, Карло. «Симметричные погружения неориентируемых регулярных отображений малого рода» (PDF). Университет Беркли.
^ Coxeter 1980, 8.3 Отображения типа {4,4} на торе.
^ Coxeter 1980, 8.4 Отображения типа {3,6} или {6,3} на торе.
^ Coxeter и Мозер, Генераторы и соотношения для дискретных групп, 1957, Глава 8, Обычные карты, 8.3 Карты типа {4,4} на торе, 8.4 Карты типа {3,6} или {6,3} на торе

Кокстер, Х. С. М.; Мозер, В. О. Дж. (1980), Генераторы и соотношения для дискретных групп, Ergebnisse der Mathematik и ихрер Гренцгебиете, 14 (4-е изд.), Springer Verlag, ISBN 978-0-387-09212-6.
ван Вейк, Ярке Дж. (2009), «Симметричная мозаика замкнутых поверхностей: визуализация регулярных карт» (PDF), Proc. СИГГРАФ (Транзакции ACM по графике), 28 (3): 12, Дои:10.1145/1531326.1531355, заархивировано из оригинал (PDF ) на 2011-06-09.
Кондер, Марстон; Dobcsányi, Peter (2001), "Определение всех регулярных карт малого рода", Журнал комбинаторной теории, серия B, 81 (2): 224–242, Дои:10.1006 / jctb.2000.2008.
Недела, Роман (2007), Карты, гиперкарты и связанные темы (PDF).
Винс, Эндрю (2004), «Карты», Справочник по теории графов.
Брем, Ульрих; Шульте, Эгон (2004), "Многогранные карты", Справочник по дискретной и вычислительной геометрии.

[1] Кокстер (1980)

[csequin-2] а ^б Секин, Карло. «Симметричные погружения неориентируемых регулярных отображений малого рода» (PDF). Университет Беркли.

[3] Coxeter 1980, 8.3 Отображения типа {4,4} на торе.

[4] Coxeter 1980, 8.4 Отображения типа {3,6} или {6,3} на торе.

[5] Coxeter и Мозер, Генераторы и соотношения для дискретных групп, 1957, Глава 8, Обычные карты, 8.3 Карты типа {4,4} на торе, 8.4 Карты типа {3,6} или {6,3} на торе

[1]

[2]

[3]

[4]

[5]