Передаточная функция FIR - FIR transfer function
Фильтр передаточной функции использует передаточную функцию и Теорема свертки изготовить фильтр. В этой статье обсуждается пример такого фильтра, использующего конечную импульсную характеристику, и показано применение фильтра в реальных данных.
FIR (Finite Impulse Response) Линейные фильтры
В цифровой обработке КИХ-фильтр - это непрерывный во времени фильтр, инвариантный со временем. Это означает, что фильтр не зависит от конкретного момента времени, а скорее зависит от продолжительности времени. В спецификации этого фильтра используется функция передачи который имеет частотную характеристику, которая будет передавать только желаемые частоты входного сигнала. Этот тип фильтра является нерекурсивным, что означает, что выходные данные могут быть полностью получены из комбинации входных данных без каких-либо рекурсивных значений выходных данных. Это означает, что нет петли обратной связи, которая передает новому выходу значения предыдущих выходов. Это преимущество перед рекурсивными фильтрами, такими как БИХ-фильтр (бесконечная импульсная характеристика) в приложениях, где требуется линейная фазовая характеристика, поскольку входной сигнал пропускается без фазовых искажений.[1]
Математическая модель
Пусть функция вывода будет и вход . Свертка входа с передаточной функцией обеспечивает отфильтрованный вывод. Математическая модель этого типа фильтра:
час() - передаточная функция импульсного отклика на вход. В свертка позволяет активировать фильтр только тогда, когда на входе записан сигнал с тем же значением времени. Этот фильтр возвращает входные значения (x (t)), если k попадает в область поддержки функции h. По этой причине этот фильтр называется конечным откликом. Если k находится за пределами области поддержки, импульсная характеристика равна нулю, что делает выход равным нулю. Центральная идея этого h () можно рассматривать как частное двух функций.[2]
По словам Хуана (1981)[3] Используя эту математическую модель, существует четыре метода проектирования нерекурсивных линейных фильтров с различными параллельные конструкции фильтров:
- Метод оформления окон
- Метод частотной выборки
- Обычное линейное программирование
- Итеративное линейное программирование
Односторонний линейный фильтр
Функция ввода
Определите входной сигнал:
добавляет случайное число от 1 до 200 к синусоидальной функции, которая служит для искажения данных.

Односторонний фильтр
Используйте экспоненциальную функцию в качестве импульсной характеристики для области поддержки положительных значений.
Амплитудно-частотная характеристика этого фильтра напоминает фильтр нижних частот как на более низкой частоте.

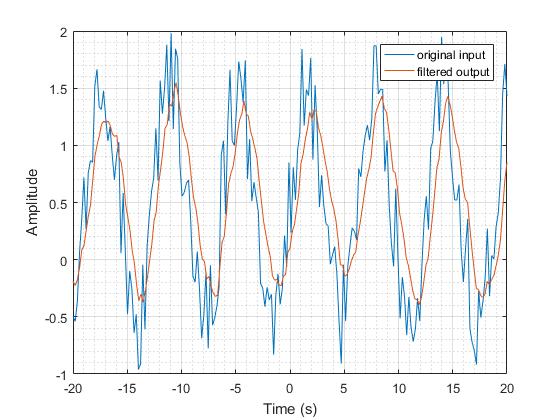
Двусторонний фильтр
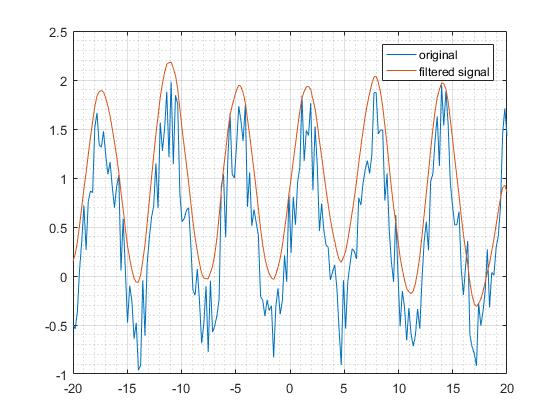
Пусть входной сигнал будет таким же, как односторонняя функция. Используйте экспоненциальную функцию в качестве импульсной характеристики для поддерживающей области положительных значений, как и раньше. В этом двустороннем фильтре также реализована другая экспоненциальная функция. Противоположность по знакам степеней экспоненты заключается в сохранении небесконечных результатов при вычислении экспоненциальных функций.
Изучите этот фильтр в его частотной области, мы увидим, что характеристика амплитуды соответствует той же тенденции, что и односторонний фильтр. Однако пропускаемые частоты меньше, чем у одностороннего фильтра. Это привело к более плавному выходу. Существенным из этого следствия является то, что типы двусторонних фильтров линейных фильтров лучше являются фильтрами.

КИХ Передаточная функция Линейный фильтр Применение
Линейный фильтр работает лучше, если это двусторонний фильтр. Это требует, чтобы данные были известны заранее, что затрудняет правильное функционирование этих фильтров в ситуациях, когда сигналы не могут быть известны заранее, например, при обработке радиосигналов. Однако это означает, что линейные фильтры чрезвычайно полезны при фильтрации предварительно загруженных данных. Кроме того, из-за своей нерекурсивной природы, которая сохраняет фазовые углы входа, линейные фильтры обычно используются в обработка изображений, обработка видео, обработка данных или обнаружение закономерностей. Некоторые примеры - улучшение изображения, восстановление и предварительное отбеливание для спектрального анализа.[4] Кроме того, линейные нерекурсивные фильтры всегда стабильны и обычно дают чисто реальный результат, что делает их более предпочтительными. Они также просты в вычислительном отношении, что обычно дает большое преимущество при использовании этого линейного КИХ-фильтра.
Рекомендации
- ^ БИХ-фильтры и КИХ-фильтры. (2012, июнь). Получено 4 мая 2017 г. из http://zone.ni.com/reference/en-XX/help/370858K-01/genmaths/genmaths/calc_filterfir_iir/
- ^ Нагаи, Н. (1990). Линейные схемы, системы и обработка сигналов: передовая теория и приложения. Нью-Йорк: М. Деккер.
- ^ Хуанг, Т. С. (1981). Темы прикладной физики: двумерная цифровая обработка сигналов I (3-е изд., Том 42, разделы прикладной физики). Берлин: Springer.
- ^ Хуанг, Т. С. (1981). Темы прикладной физики: двумерная цифровая обработка сигналов I (3-е изд., Том 42, разделы прикладной физики). Берлин: Springer.









