Обобщенная логистическая функция - Generalised logistic function

A = 0, K = 1, B = 3, Q = ν = 0,5, M = 0, C = 1

Влияние изменения параметра A. Все остальные параметры равны 1.

Влияние изменения параметра B. A = 0, все остальные параметры равны 1.

Влияние изменения параметра C. A = 0, все остальные параметры равны 1.

Влияние изменения параметра K. A = 0, все остальные параметры равны 1.

Влияние изменения параметра Q. A = 0, все остальные параметры равны 1.

Влияние переменного параметра

{ displaystyle nu}

. A = 0, все остальные параметры равны 1.

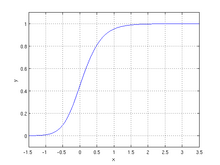
В обобщенная логистическая функция или же изгиб, также известный как Кривая Ричардса, первоначально разработанная для моделирования роста, является расширением логистика или же сигмовидный функции, позволяющие создавать более гибкие S-образные кривые:

{ Displaystyle Y (T) = A + {K-A over (C + Qe ^ {- Bt}) ^ {1 / nu}}}

куда ${ displaystyle Y}$ = вес, рост, размер и т. д., и ${ displaystyle t}$ = время.

У него пять параметров:

${ displaystyle A}$ : нижняя асимптота;
${ displaystyle K}$ : верхняя асимптота при ${ displaystyle C = 1}$ . Если ${ displaystyle A = 0}$ и ${ displaystyle C = 1}$ тогда ${ displaystyle K}$ называется грузоподъемность;
${ displaystyle B}$ : скорость роста;
${ displaystyle nu> 0}$ : влияет на то, вблизи какой асимптоты происходит максимальный рост.
${ displaystyle Q}$ : связано со значением ${ displaystyle Y (0)}$
${ displaystyle C}$ : обычно принимает значение 1. В противном случае верхняя асимптота ${ displaystyle A + {K-A over C ^ { nu}}}$

Уравнение также можно записать:

{ Displaystyle Y (т) = А + {К-А над (С + е ^ {- В (т-М)}) ^ {1 / nu}}}

куда ${ displaystyle M}$ можно рассматривать как время начала, ${ displaystyle t_ {0}}$ (при этом ${ displaystyle Y (t_ {0}) = A + {K-A over (C + 1) ^ {1 / nu}}}$ )

Включая оба ${ displaystyle Q}$ и ${ displaystyle M}$ может быть удобно:

{ Displaystyle Y (т) = А + {К-А над (С + Qe ^ {- В (т-М)}) ^ {1 / nu}}}

это представление упрощает установку как времени начала, так и значения Y в это время.

Общую модель иногда называют «кривой Ричардса» в честь Ф. Дж. Ричардса, который в 1959 году предложил общую форму для семейства моделей.

В логистика, с максимальной скоростью роста за время ${ displaystyle M}$ , это случай, когда ${ Displaystyle Q = nu = 1}$ .

Обобщенное логистическое дифференциальное уравнение

Частный случай обобщенной логистической функции:

{ Displaystyle Y (T) = {К над (1 + Qe ^ {- alpha nu (t-t_ {0})}) ^ {1 / nu}}}

которое является решением дифференциального уравнения Ричардса (RDE):

{ displaystyle Y ^ { prime} (t) = alpha left (1- left ({ frac {Y} {K}} right) ^ { nu} right) Y}

с начальным условием

{ Displaystyle Y (t_ {0}) = Y_ {0}}

куда

{ displaystyle Q = -1 + left ({ frac {K} {Y_ {0}}} right) ^ { nu}}

при условии, что ν> 0 и α> 0.

Классическое логистическое дифференциальное уравнение является частным случаем указанного выше уравнения с ν = 1, тогда как Кривая Гомперца можно восстановить в пределе ${ displaystyle nu rightarrow 0 ^ {+}}$ при условии, что:

{ displaystyle alpha = O left ({ frac {1} { nu}} right)}

На самом деле при малых ν это

{ displaystyle Y ^ { prime} (t) = Yr { frac {1- exp left ( nu ln left ({ frac {Y} {K}} right) right)} { nu}} приблизительно rY ln left ({ frac {Y} {K}} right)}

RDE моделирует многие феномены роста, включая рост опухолей. В онкологии его основные биологические особенности аналогичны таковым у Логистическая кривая модель.

Модели RDE широко используются для описания траектории инфекции в эпидемиологическом моделировании; видеть [1] для приложения COVID-19.

Градиент обобщенной логистической функции

При оценке параметров на основе данных часто необходимо вычислить частные производные логистической функции по параметрам в данной точке данных. ${ displaystyle t}$ (видеть ^[1]). Для случая, когда ${ displaystyle C = 1}$ ,

{ displaystyle { begin {align} { frac { partial Y} { partial A}} & = 1- (1 + Qe ^ {- B (tM)}) ^ {- 1 / nu} { frac { partial Y} { partial K}} & = (1 + Qe ^ {- B (tM)}) ^ {- 1 / nu} { frac { частичный Y} { partial B}} & = { frac {(KA) (tM) Qe ^ {- B (tM)}} { nu (1 + Qe ^ {- B (tM)}) ^ {{ frac {1} { nu}} + 1}}} { frac { partial Y} { partial nu}} & = { frac {(KA) ln (1 + Qe ^ {-B (tM)})} { nu ^ {2} (1 + Qe ^ {- B (tM)}) ^ { frac {1} { nu}}}} { frac { partial Y} { partial Q}} & = - { frac {(KA) e ^ {- B (tM)}} { nu (1 + Qe ^ {- B (tM)}) ^ {{ frac {1} { nu}} + 1}}} { frac { partial Y} { partial M}} & = - { frac {(KA) QBe ^ {- B (tM )}} { nu (1 + Qe ^ {- B (tM)}) ^ {{ frac {1} { nu}} + 1}}} конец {выровнено}}}

Применение к эпидемиологическому моделированию COVID-19

Роль параметра формы

{ Displaystyle xi}

в обобщенной логистической функции

Роли трех параметров в обобщенной логистической функции

Обобщенная логистическая функция (Кривая роста Ричардса) широко используется при моделировании COVID-19 траектории заражения.^[2] Траектория заражения - это (обычно ежедневные) данные временного ряда для совокупного числа инфицированных случаев для субъекта. Темой может быть определенная страна, город, штат и т. Д. В литературе есть варианты перенастройки параметров, и одна из часто используемых форм -

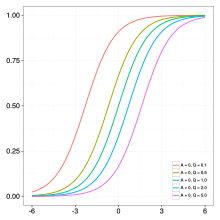
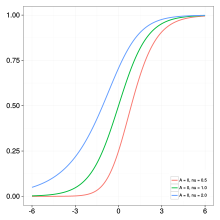
${ Displaystyle е (T; theta _ {1}, theta _ {2}, theta _ {3}, xi) = theta _ {1} cdot [1+ xi cdot exp {- theta _ {2} cdot (t- theta _ {3}) }] ^ {- 1 / xi}}$

куда ${ displaystyle theta _ {1}, theta _ {2}, theta _ {3}}$ настоящие числа, и ${ Displaystyle xi}$ положительное действительное число. Гибкость кривой ${ displaystyle f}$ обусловлено параметром ${ Displaystyle xi}$ : (i) если ${ Displaystyle xi = 1}$ тогда кривая сводится к логистической функции, и (ii) если ${ Displaystyle xi}$ сходится к нулю, то кривая сходится к Функция Гомперца. В эпидемиологическом моделировании параметры ${ displaystyle theta _ {1}}$ , ${ displaystyle theta _ {2}}$ , и ${ displaystyle theta _ {3}}$ представляют окончательный размер эпидемии, уровень заражения, и фаза задержки, соответственно. См. Правые панели для графического описания примерной траектории заражения, когда ${ displaystyle ( theta _ {1}, theta _ {2}, theta _ {3})}$ обозначены ${ displaystyle (10,000,0.2,40)}$ при изменении ${ Displaystyle xi}$ быть ${ displaystyle 1 times 10 ^ {- 13} приблизительно 0}$ , ${ displaystyle 0.5}$ , и ${ displaystyle 1}$ , соответственно.