Сигмовидная функция - Википедия - Sigmoid function

В логистическая кривая

Сюжет о функция ошибки

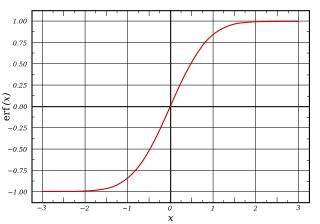
А сигмовидная функция это математическая функция имеющий характерную S-образную кривую или сигмовидная кривая. Типичным примером сигмовидной функции является логистическая функция показано на первом рисунке и определяется формулой:^[1]

${ displaystyle S (x) = { frac {1} {1 + e ^ {- x}}} = { frac {e ^ {x}} {e ^ {x} +1}}.}$

Другие стандартные сигмовидные функции приведены в Раздел примеров.

Особые случаи сигмовидной функции включают Кривая Гомперца (используется в системах моделирования, которые насыщаются при больших значениях x) и кривая ogee (используется в водосброс некоторых плотины ). Сигмовидные функции имеют область всех действительные числа, обычно с возвращаемым (ответным) значением монотонно возрастающий но может уменьшаться. Сигмоидные функции чаще всего показывают возвращаемое значение (ось y) в диапазоне от 0 до 1. Другой часто используемый диапазон - от -1 до 1.

Широкий спектр сигмовидных функций, включая логистические и гиперболический тангенс функции использовались как функция активации из искусственные нейроны. Сигмовидные кривые также распространены в статистике как кумулятивные функции распределения (которые меняются от 0 до 1), например, интегралы от логистическая плотность, то нормальная плотность, и Студенты т функции плотности вероятности. Логистическая сигмоидальная функция обратима, а обратная ей - логит функция.

Определение

Сигмовидная функция - это ограниченный, дифференцируемый, действительная функция, которая определена для всех реальных входных значений и имеет неотрицательную производную в каждой точке^[1] и ровно одна точка перегиба. Сигмовидная «функция» и сигмовидная «кривая» относятся к одному и тому же объекту.

Характеристики

В общем, сигмовидная функция монотонный, и имеет первый производная который в форме колокола. И наоборот, интеграл любой непрерывной неотрицательной колоколообразной функции (с одним локальным максимумом и без локального минимума, если только она не вырождена) будет сигмоидальной. Таким образом кумулятивные функции распределения для многих общих распределения вероятностей сигмовидные. Одним из таких примеров является функция ошибки, которая связана с кумулятивной функцией распределения нормальное распределение.

Сигмовидная функция ограничена парой горизонтальные асимптоты в качестве ${ Displaystyle х rightarrow pm infty}$.

Сигмовидная функция - это выпуклый для значений меньше 0, и это вогнутый для значений больше 0.

Примеры

Сравнение некоторых сигмовидных функций. На чертеже все функции нормализованы таким образом, что их наклон в начале координат равен 1.

• Логистическая функция

${ displaystyle f (x) = { frac {1} {1 + e ^ {- x}}}}$

• Гиперболический тангенс (смещенная и масштабированная версия логистической функции выше)

${ displaystyle f (x) = tanh x = { frac {e ^ {x} -e ^ {- x}} {e ^ {x} + e ^ {- x}}}}$

• Функция арктангенса

${ displaystyle f (x) = arctan x}$

• Функция Гудермана

${ displaystyle f (x) = operatorname {gd} (x) = int _ {0} ^ {x} { frac {1} { ch t}} , dt = 2 arctan left ( tanh left ({ frac {x} {2}} right) right)}$

• Функция ошибки

${ displaystyle f (x) = operatorname {erf} (x) = { frac {2} { sqrt { pi}}} int _ {0} ^ {x} e ^ {- t ^ {2 }} , dt}$

• Обобщенная логистическая функция

${ Displaystyle е (х) = (1 + е ^ {- х}) ^ {- альфа}, квад альфа> 0}$

• Плавный шаг функция

${ Displaystyle е (х) = { begin {case} displaystyle { left ( int _ {0} ^ {1} (1-u ^ {2}) ^ {N} du right) ^ { -1} int _ {0} ^ {x} (1-u ^ {2}) ^ {N} du}, & | x | leq 1 \ имя оператора {sgn} (x) & | x | geq 1 end {case}} , quad N geq 1}$

• Немного алгебраические функции, Например

${ displaystyle f (x) = { frac {x} { sqrt {1 + x ^ {2}}}}}$

Приложения

Перевернутая логистическая S-кривая для моделирования зависимости между урожайностью пшеницы и засолением почвы. ^[2]

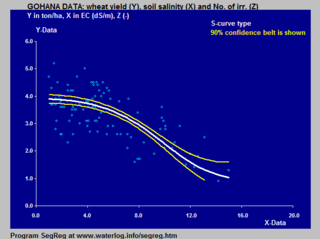
Многие природные процессы, например сложные системы кривые обучения, демонстрируют прогрессию от маленького начала, которая со временем ускоряется и приближается к кульминации. Когда конкретная математическая модель отсутствует, часто используется сигмовидная функция.^[3]

В модель ван Генухтена – Гупты основан на перевернутой S-образной кривой и применяется к ответу урожайности на засоление почвы.

Примеры применения логистической S-кривой к реакции урожайности (пшеницы) как на засоление почвы, так и на глубину уровень грунтовых вод в почве показаны на логистическая функция # В сельском хозяйстве: моделирование реакции сельскохозяйственных культур.

В искусственные нейронные сети, иногда вместо них для повышения эффективности используются негладкие функции; они известны как твердые сигмоиды.

В обработка аудиосигнала, сигмовидные функции используются как волновод передаточные функции подражать звуку аналоговая схема вырезка.^[4]

В биохимия и фармакология, то Уравнение Хилла и уравнение Хилла – Ленгмюра являются сигмоидальными функциями.

В компьютерной графике и рендеринге в реальном времени некоторые сигмовидные функции используются для плавного смешивания цветов или геометрии между двумя значениями без видимых швов или разрывов.

Кривые титрования между сильными кислотами и сильными основаниями имеют сигмовидную форму из-за логарифмической природы шкала pH.

Смотрите также

Рекомендации

• Митчелл, Том М. (1997). Машинное обучение. WCB – McGraw – Hill. ISBN  978-0-07-042807-2.. В частности, см. «Главу 4: Искусственные нейронные сети» (в частности, стр. 96–97), где Митчелл использует слова «логистическая функция» и «сигмовидная функция» как синонимы - эту функцию он также называет «функцией сжатия» - и сигмоидная (также известная как логистическая) функция используется для сжатия выходных сигналов «нейронов» в многослойных нейронных сетях.
• Хамфрис, Марк. «Непрерывный вывод, сигмовидная функция». Свойства сигмоида, включая то, как он может сдвигаться по осям и как его домен может быть преобразован.