Искусственный нейрон - Artificial neuron

An искусственный нейрон это математическая функция задуман как модель биологических нейроны, а нейронная сеть. Искусственные нейроны - это элементарные единицы в искусственная нейронная сеть.^[1] Искусственный нейрон получает один или несколько входных сигналов (представляющих возбуждающие постсинаптические потенциалы и тормозные постсинаптические потенциалы на нервной дендриты ) и суммирует их, чтобы получить результат (или активация, представляющий нейрон потенциал действия который передается по его аксон ). Обычно каждый вход отдельно взвешенный, а сумма пропускается через нелинейная функция известный как функция активации или же функция передачи^{[требуется разъяснение ]}. Передаточные функции обычно имеют сигмовидная форма, но они также могут принимать форму других нелинейных функций, кусочно линейные функции, или пошаговые функции. Они также часто монотонно возрастающий, непрерывный, дифференцируемый и ограниченный. Функция порога вдохновила создание логические ворота называется пороговой логикой; применимо к строительству логические схемы напоминающий обработку мозга. Например, новые устройства, такие как мемристоры в последнее время широко использовались для разработки такой логики.^[2]

Не следует путать передаточную функцию искусственного нейрона с функцией линейной системы. функция передачи.

Базовая структура

Для данного искусственного нейрона k пусть существует м + 1 вход с сигналами Икс₀ через Икс_м и веса ш_k0 через ш_kм. Обычно Икс₀ входу присваивается значение +1, что делает его предвзятость ввод с ш_k0 = б_k. Остается только м фактические входы в нейрон: от Икс₁ к Икс_м.

Выход k-й нейрон:

${ displaystyle y_ {k} = varphi left ( sum _ {j = 0} ^ {m} w_ {kj} x_ {j} right)}$

Где ${ displaystyle varphi}$ (phi) - передаточная функция (обычно пороговая функция).

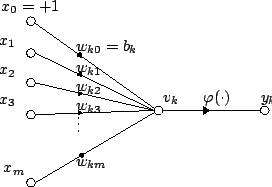
Выход аналогичен выходу аксон биологического нейрона, и его значение распространяется на вход следующего слоя через синапс. Он также может выйти из системы, возможно, как часть вывода вектор.

У него нет процесса обучения как такового. Рассчитываются его веса передаточной функции и предварительно определяется пороговое значение.

Типы

В зависимости от конкретной используемой модели их можно назвать полулинейный блок, Nv нейрон, бинарный нейрон, линейная пороговая функция, или же Маккаллох – Питтс (MCP) нейрон.

Простые искусственные нейроны, такие как модель Маккаллоха-Питтса, иногда называют «карикатурными моделями», поскольку они предназначены для отражения одного или нескольких нейрофизиологических наблюдений, но без учета реализма.^[3]

Эта секция нуждается в расширении. Вы можете помочь добавляя к этому. (Май 2017 г.)

Биологические модели

Нейрон и миелинизированный аксон, с потоком сигналов от входов дендритов к выходам на терминалах аксонов

Искусственные нейроны созданы для имитации аспектов своих биологических аналогов.

• Дендриты - В биологическом нейроне дендриты действуют как входной вектор. Эти дендриты позволяют клетке получать сигналы от большого (> 1000) числа соседних нейронов. Как и в приведенной выше математической обработке, каждый дендрит может выполнять «умножение» на «значение веса» этого дендрита. Размножение достигается за счет увеличения или уменьшения отношения синаптических нейромедиаторов к сигнальным химическим веществам, введенным в дендрит в ответ на синаптический нейромедиатор. Отрицательный эффект умножения может быть достигнут путем передачи ингибиторов сигнала (т.е. противоположно заряженных ионов) вдоль дендрита в ответ на прием синаптических нейромедиаторов.
• Сома - В биологическом нейроне сома действует как функция суммирования, как видно из приведенного выше математического описания. Когда положительные и отрицательные сигналы (возбуждающие и подавляющие соответственно) поступают в сому от дендритов, положительные и отрицательные ионы эффективно суммируются, просто благодаря тому, что они смешиваются вместе в растворе внутри тела клетки.
• Аксон - Аксон получает сигнал в результате суммирования, происходящего внутри сомы. Отверстие к аксону по существу измеряет электрический потенциал раствора внутри сомы. Как только сома достигает определенного потенциала, аксон будет передавать общий импульс сигнала по всей своей длине. В этом отношении аксон действует как способность соединять наш искусственный нейрон с другими искусственными нейронами.

Однако, в отличие от большинства искусственных нейронов, биологические нейроны срабатывают дискретными импульсами. Каждый раз, когда электрический потенциал внутри сомы достигает определенного порога, по аксону передается импульс. Эта пульсация может быть преобразована в непрерывные значения. Скорость (активаций в секунду и т. Д.), С которой активируется аксон, напрямую преобразуется в скорость, с которой соседние клетки получают вводимые в них сигнальные ионы. Чем быстрее срабатывает биологический нейрон, тем быстрее соседние нейроны накапливают электрический потенциал (или теряют электрический потенциал, в зависимости от «веса» дендрита, который соединяется с активированным нейроном). Именно это преобразование позволяет ученым-информатикам и математикам моделировать биологические нейронные сети с использованием искусственных нейронов, которые могут выводить различные значения (часто от -1 до 1).

Кодирование

Исследования показали, что унарное кодирование используется в нейронных цепях, отвечающих за пение птиц производство.^[4][5] Использование унарных в биологических сетях предположительно связано с присущей простотой кодирования. Еще одним фактором может быть то, что унарное кодирование обеспечивает определенную степень исправления ошибок.^[6]

История

Первым искусственным нейроном был пороговый логический блок (ВПУ) или линейный пороговый блок.^[7] впервые предложено Уоррен МакКаллох и Уолтер Питтс в 1943 году. Модель была специально предназначена как вычислительная модель «нервной сети» в мозге.^[8] В качестве передаточной функции использовался порог, эквивалентный использованию Ступенчатая функция Хевисайда. Первоначально рассматривалась только простая модель с двоичными входами и выходами, некоторыми ограничениями на возможные веса и более гибким пороговым значением. С самого начала уже было замечено, что любые логическая функция могут быть реализованы сетями таких устройств, что легко увидеть из того факта, что можно реализовать функции И и ИЛИ и использовать их в дизъюнктивный или конъюнктивная нормальная форма Вскоре исследователи также поняли, что циклические сети с отзывы через нейроны, можно было бы определять динамические системы с памятью, но большая часть исследований концентрировалась (и до сих пор делает) строго сети прямого распространения из-за меньшей сложности, которую они представляют.

Одной из важных и новаторских искусственных нейронных сетей, в которых использовалась линейная пороговая функция, была перцептрон, разработан Фрэнк Розенблатт. Эта модель уже учитывала более гибкие значения веса в нейронах и использовалась в машинах с адаптивными возможностями. Представление пороговых значений в виде смещения было введено Бернард Видроу в 1960 - см. АДАЛИН.

В конце 1980-х, когда исследования нейронных сетей набрали силу, стали рассматриваться нейроны более непрерывной формы. Возможность дифференцирования функции активации позволяет напрямую использовать градиентный спуск и другие алгоритмы оптимизации для настройки весов. Нейронные сети также начали использоваться в качестве общего аппроксимация функции модель. Самый известный алгоритм обучения называется обратное распространение был переоткрыт несколько раз, но его первая разработка восходит к работе Пол Вербос.^[9][10]

Типы передаточных функций

Было предложено, чтобы этот раздел был расколоть в другую статью под названием функция передачи. (Обсуждать) (Май 2017 г.)

Передаточная функция (функция активации ) нейрона выбирается так, чтобы он обладал рядом свойств, которые либо улучшают, либо упрощают сеть, содержащую нейрон. Крайне важно, например, любое многослойный персептрон используя линейный передаточная функция имеет эквивалентную одноуровневую сеть; Поэтому для получения преимуществ многоуровневой сети необходима нелинейная функция.^{[нужна цитата ]}

Ниже, ты во всех случаях относится к взвешенной сумме всех входов нейрона, т.е. п входы,

${ Displaystyle и = сумма _ {я = 1} ^ {п} ш_ {я} х_ {я}}$

куда ш вектор синаптические веса и Икс - вектор входов.

Ступенчатая функция

Выход у этой передаточной функции является двоичным, в зависимости от того, соответствует ли вход заданному порогу, θ. «Сигнал» отправляется, т.е. выход устанавливается в единицу, если активация соответствует пороговому значению.

${ displaystyle y = { begin {case} 1 & { text {if}} u geq theta 0 & { text {if}} u < theta end {cases}}}$

Эта функция используется в перцептроны и часто встречается во многих других моделях. Он выполняет разделение Космос вкладов гиперплоскость. Это особенно полезно на последнем уровне сети, предназначенном для выполнения двоичной классификации входов. Его можно аппроксимировать из других сигмоидальных функций, присвоив весам большие значения.

Линейная комбинация

В этом случае единица вывода - это просто взвешенная сумма его входов плюс предвзятость срок. Ряд таких линейных нейронов выполняет линейное преобразование входного вектора. Обычно это более полезно на первых уровнях сети. Существует ряд инструментов анализа, основанных на линейных моделях, таких как гармонический анализ, и все они могут использоваться в нейронных сетях с этим линейным нейроном. Термин смещения позволяет нам сделать аффинные преобразования к данным.

Видеть: Линейное преобразование, Гармонический анализ, Линейный фильтр, Вейвлет, Анализ главных компонентов, Независимый компонентный анализ, Деконволюция.

Сигмовидная

Достаточно простая нелинейная функция сигмовидная функция такая как логистическая функция, также имеет легко вычисляемую производную, что может быть важно при вычислении обновлений веса в сети. Таким образом, это упрощает математическое манипулирование сетью и было привлекательно для первых компьютерных ученых, которым требовалось минимизировать вычислительную нагрузку при моделировании. Ранее это обычно видели в многослойные персептроны. Однако недавняя работа показала, что сигмовидные нейроны менее эффективны, чем выпрямленный линейный нейроны. Причина в том, что градиенты, вычисленные обратное распространение Алгоритм имеет тенденцию уменьшаться до нуля по мере того, как активации распространяются через слои сигмоидальных нейронов, что затрудняет оптимизацию нейронных сетей с использованием нескольких слоев сигмоидальных нейронов.

Выпрямитель

В контексте искусственные нейронные сети, то выпрямитель является функция активации определяется как положительная часть его аргумента:

${ Displaystyle е (х) = х ^ {+} = макс (0, х),}$

куда Икс это вход в нейрон. Это также известно как функция рампы и аналогичен полуволновое выпрямление в электротехнике. Этот функция активации был впервые представлен в динамической сети Ханлозером и др. в статье 2000 года в Nature^[11] с сильным биологический мотивации и математические обоснования.^[12] Это было впервые продемонстрировано в 2011 году, чтобы обеспечить лучшее обучение более глубоких сетей,^[13] по сравнению с широко используемыми функциями активации до 2011 г., т.е. логистическая сигмовидная (вдохновленный теория вероятности; видеть логистическая регрессия ) и его более практичный^[14] коллега, гиперболический тангенс.

Алгоритм псевдокода

Было предложено, чтобы этот раздел был расколоть в другую статью под названием Пороговая логическая единица. (Обсуждать) (Май 2017 г.)

Ниже приводится простой псевдокод реализация единого TLU, который требует логический input (true или false), и при активации возвращает единственный логический вывод. An объектно-ориентированный модель используется. Метод обучения не определен, поскольку существует несколько. Если бы использовалась чисто функциональная модель, приведенный ниже класс TLU был бы заменен функциональным TLU с порогом входных параметров, весами и входными данными, которые возвращали логическое значение.

учебный класс ВПУ определяется как:    член данных порог : номер член данных веса : Список числа размера Икс функциональный член огонь (входы : Список булевы размера ИКС) : логический определяется как:        Переменная Т : число Т ← 0        для каждого я в 1 к Икс делать            если входы (я) является истинный тогда                Т ← T + веса (i) конец, если        конец для каждого        если T> порог тогда            возвращаться истинный еще:            возвращаться ложный конец, если    конечная функцияконец класса

Смотрите также

• Связывающий нейрон
• Коннекционизм

Рекомендации

дальнейшее чтение

внешняя ссылка

• Искусственный [sic] нейрон имитирует функцию клеток человека
• McCulloch-Pitts Neurons (Обзор)