Градиентный спуск - Gradient descent

Градиентный спуск это Первый заказ итеративный оптимизация алгоритм для поиска местный минимум дифференцируемой функции. Идея состоит в том, чтобы повторять шаги в противоположном направлении градиент (или приблизительный градиент) функции в текущей точке, потому что это направление наискорейшего спуска. И наоборот, переход в направлении градиента приведет к локальный максимум этой функции; процедура тогда известна как градиентный подъем.

Градиентный спуск обычно приписывают Коши, который впервые предложил это в 1847 году,^[1] но его свойства сходимости для задач нелинейной оптимизации были впервые изучены Хаскелл Карри в 1944 г.^[2]

Описание

Иллюстрация градиентного спуска на серии наборы уровней

Градиентный спуск основан на наблюдении, что если функция с несколькими переменными ${ Displaystyle F ( mathbf {x})}$ является определенный и дифференцируемый в окрестности точки ${ Displaystyle mathbf {а}}$ , тогда ${ Displaystyle F ( mathbf {x})}$ уменьшается самый быстрый если один идет от ${ Displaystyle mathbf {а}}$ в направлении отрицательного градиента ${ displaystyle F}$ в ${ displaystyle mathbf {a}, - nabla F ( mathbf {a})}$ . Отсюда следует, что если

{ displaystyle mathbf {a} _ {n + 1} = mathbf {a} _ {n} - gamma nabla F ( mathbf {a} _ {n})}

за ${ displaystyle gamma in mathbb {R} _ {+}}$ достаточно маленький, тогда ${ Displaystyle F ( mathbf {a_ {n}}) geq F ( mathbf {a_ {n + 1}})}$ . Другими словами, термин ${ Displaystyle гамма набла F ( mathbf {а})}$ вычитается из ${ Displaystyle mathbf {а}}$ потому что мы хотим двигаться против градиента, к локальному минимуму. Имея в виду это наблюдение, можно начать с предположения ${ displaystyle mathbf {x} _ {0}}$ за местный минимум ${ displaystyle F}$ , и рассматривает последовательность ${ displaystyle mathbf {x} _ {0}, mathbf {x} _ {1}, mathbf {x} _ {2}, ldots}$ такой, что

{ displaystyle mathbf {x} _ {n + 1} = mathbf {x} _ {n} - gamma _ {n} nabla F ( mathbf {x} _ {n}), n geq 0.}

У нас есть монотонный последовательность

{ Displaystyle F ( mathbf {x} _ {0}) geq F ( mathbf {x} _ {1}) geq F ( mathbf {x} _ {2}) geq cdots,}

так надеюсь последовательность ${ displaystyle ( mathbf {x} _ {n})}$ сходится к желаемому локальному минимуму. Обратите внимание, что значение размер шага ${ displaystyle gamma}$ может изменяться на каждой итерации. При определенных предположениях о функции ${ displaystyle F}$ (Например, ${ displaystyle F}$ выпуклый и ${ displaystyle nabla F}$ Липшиц ) и конкретный выбор ${ displaystyle gamma}$ (например, выбранный либо через линейный поиск что удовлетворяет Условия Вульфа, или метод Барзилаи – Борвейна^[3]^[4] показано ниже),

{ displaystyle gamma _ {n} = { frac { left | left ( mathbf {x} _ {n} - mathbf {x} _ {n-1} right) ^ {T} left [ nabla F ( mathbf {x} _ {n}) - nabla F ( mathbf {x} _ {n-1}) right] right |} { left | nabla F ( mathbf {x} _ {n}) - nabla F ( mathbf {x} _ {n-1}) right | ^ {2}}}}

конвергенция до местного минимума может быть гарантировано. Когда функция ${ displaystyle F}$ является выпуклый, все локальные минимумы также являются глобальными минимумами, поэтому в этом случае градиентный спуск может сходиться к глобальному решению.

Этот процесс показан на картинке рядом. Здесь ${ displaystyle F}$ считается определенным на плоскости, а его график имеет чаша форма. Синие кривые - это контурные линии, то есть регионы, на которых значение ${ displaystyle F}$ постоянно. Красная стрелка, исходящая из точки, показывает направление отрицательного градиента в этой точке. Обратите внимание, что (отрицательный) градиент в точке равен ортогональный к линии контура, проходящей через эту точку. Мы видим этот градиент спуск приводит нас к дну чаши, то есть к точке, где значение функции ${ displaystyle F}$ минимально.

Аналогия для понимания градиентного спуска

Туман в горах

Основная интуиция градиентного спуска может быть проиллюстрирована гипотетическим сценарием. Человек застрял в горах и пытается спуститься (т.е. пытается найти глобальный минимум). Сильный туман, поэтому видимость крайне низкая. Следовательно, путь вниз с горы не виден, поэтому они должны использовать местную информацию, чтобы найти минимум. Они могут использовать метод градиентного спуска, который включает в себя рассмотрение крутизны холма в их текущем положении, а затем движение в направлении самого крутого спуска (т. Е. Под гору). Если бы они пытались найти вершину горы (т. Е. Максимум), то они бы продолжили движение в направлении наиболее крутого подъема (т. Е. В гору). Используя этот метод, они в конечном итоге могли спуститься с горы или, возможно, застряли в какой-нибудь дыре (т.е. локальный минимум или точка перевала ), как горное озеро. Однако предположим также, что крутизна холма не сразу очевидна при простом наблюдении, а, скорее, для ее измерения требуется сложный инструмент, который у человека есть в данный момент. Чтобы измерить крутизну холма с помощью прибора, требуется некоторое время, поэтому им следует свести к минимуму использование прибора, если они хотят спуститься с горы до захода солнца. Тогда сложность состоит в том, чтобы выбрать частоту, с которой они должны измерять крутизну холма, чтобы не сбиться с пути.

В этой аналогии человек представляет алгоритм, а путь вниз по горе представляет собой последовательность настроек параметров, которые алгоритм будет исследовать. Крутизна холма представляет собой склон поверхности ошибки в этой точке. Инструмент, используемый для измерения крутизны дифференциация (наклон поверхности ошибки можно рассчитать, взяв производная функции квадрата ошибки в этой точке). Направление, которое они выбирают, совпадает с градиент поверхности ошибки в этой точке. Время, которое они проходят до следующего измерения, - это скорость обучения алгоритма. Видеть Обратное распространение § Ограничения для обсуждения ограничений этого типа алгоритма "спуска по холму".

Примеры

Градиентный спуск имеет проблемы с патологическими функциями, такими как Функция Розенброка показано здесь.

{ displaystyle f (x_ {1}, x_ {2}) = (1-x_ {1}) ^ {2} +100 (x_ {2} - {x_ {1}} ^ {2}) ^ {2 }.}

Функция Розенброка имеет узкую изогнутую долину, которая содержит минимум. Дно долины очень плоское. Из-за изогнутой плоской впадины оптимизация идет медленно, с небольшими шагами к минимуму.

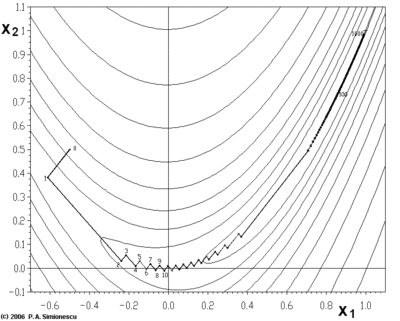
Зигзагообразный характер метода также очевиден ниже, где метод градиентного спуска применяется к

{ displaystyle F (x, y) = sin left ({ frac {1} {2}} x ^ {2} - { frac {1} {4}} y ^ {2} +3 right ) cos left (2x + 1-e ^ {y} right).}

Выбор размера шага и направления спуска

Поскольку размер шага ${ displaystyle gamma}$ слишком маленький будет замедлять сходимость, а ${ displaystyle gamma}$ слишком большой приведет к расхождению, поиск хорошей настройки ${ displaystyle gamma}$ это важная практическая проблема. Филип Вулф также выступал за использование «умного выбора направления [спуска]» на практике.^[5] Хотя использование направления, которое отклоняется от направления самого крутого спуска, может показаться нелогичным, идея состоит в том, что меньший уклон можно компенсировать, выдерживая гораздо большее расстояние.

Чтобы рассуждать об этом математически, давайте воспользуемся направлением ${ displaystyle mathbf {p} _ {n}}$ и размер шага ${ displaystyle gamma _ {n}}$ и рассмотрим более общее обновление:

{ displaystyle mathbf {a} _ {n + 1} = mathbf {a} _ {n} - gamma _ {n} , mathbf {p} _ {n}}

.

Поиск хороших настроек ${ displaystyle mathbf {p} _ {n}}$ и ${ displaystyle gamma _ {n}}$ требуется немного подумать. Прежде всего, нам бы хотелось, чтобы направление обновления было под гору. Математически, позволяя ${ displaystyle theta _ {n}}$ обозначают угол между ${ Displaystyle набла Ф ( mathbf {а_ {п}})}$ и ${ displaystyle mathbf {p} _ {n}}$ , для этого требуется, чтобы ${ displaystyle cos theta _ {n}> 0.}$ Чтобы сказать больше, нам нужно больше информации о целевой функции, которую мы оптимизируем. При достаточно слабом предположении, что ${ displaystyle F}$ непрерывно дифференцируемо, можно доказать, что:^[6]

{ Displaystyle F ( mathbf {a} _ {n + 1}) leq F ( mathbf {a} _ {n}) - gamma _ {n} | nabla F ( mathbf {a} _ {n}) | _ {2} | mathbf {p} _ {n} | _ {2} left [ cos theta _ {n} - max _ {t in [0,1 ]} { frac { | nabla F ( mathbf {a} _ {n} -t gamma _ {n} mathbf {p} _ {n}) - nabla F ( mathbf {a} _ {n}) | _ {2}} { | nabla F ( mathbf {a} _ {n}) | _ {2}}} right]}

(1)

Из этого неравенства следует, что величина, по которой мы можем быть уверены, что функция ${ displaystyle F}$ уменьшается в зависимости от компромисса между двумя терминами в квадратных скобках. Первый член в квадратных скобках измеряет угол между направлением спуска и отрицательным градиентом. Второй член измеряет, насколько быстро меняется градиент по направлению спуска.

В принципе неравенство (1) можно оптимизировать ${ displaystyle mathbf {p} _ {n}}$ и ${ displaystyle gamma _ {n}}$ выбрать оптимальный размер и направление шага. Проблема в том, что оценка второго члена в квадратных скобках требует оценки ${ Displaystyle набла F ( mathbf {a} _ {n} -t gamma _ {n} mathbf {p} _ {n})}$ , а дополнительные оценки градиента обычно дороги и нежелательны. Вот несколько способов обойти эту проблему:

Откажитесь от преимуществ грамотного направления спуска, установив ${ displaystyle mathbf {p} _ {n} = nabla F ( mathbf {a_ {n}})}$ , и используйте линейный поиск найти подходящий размер шага ${ displaystyle gamma _ {n}}$ , например тот, который удовлетворяет Условия Вульфа.
При условии, что ${ displaystyle F}$ дважды дифференцируема, воспользуемся ее гессианом ${ displaystyle nabla ^ {2} F}$ чтобы оценить ${ displaystyle | nabla F ( mathbf {a} _ {n} -t gamma _ {n} mathbf {p} _ {n}) - nabla F ( mathbf {a} _ {n} ) | _ {2} приблизительно | t gamma _ {n} nabla ^ {2} F ( mathbf {a} _ {n}) mathbf {p} _ {n} |.}$ Тогда выбирай ${ displaystyle mathbf {p} _ {n}}$ и ${ displaystyle gamma _ {n}}$ за счет оптимизации неравенства (1).
При условии, что ${ displaystyle nabla F}$ является Липшиц, используйте его константу Липшица ${ displaystyle L}$ связывать ${ displaystyle | nabla F ( mathbf {a} _ {n} -t gamma _ {n} mathbf {p} _ {n}) - nabla F ( mathbf {a} _ {n} ) | _ {2} leq Lt gamma _ {n} | mathbf {p} _ {n} |.}$ Тогда выбирай ${ displaystyle mathbf {p} _ {n}}$ и ${ displaystyle gamma _ {n}}$ за счет оптимизации неравенства (1).
Создайте собственную модель ${ displaystyle max _ {t in [0,1]} { frac { | nabla F ( mathbf {a} _ {n} -t gamma _ {n} mathbf {p} _ { n}) - nabla F ( mathbf {a} _ {n}) | _ {2}} { | nabla F ( mathbf {a} _ {n}) | _ {2}}} }$ за ${ displaystyle F}$ . Тогда выбирай ${ displaystyle mathbf {p} _ {n}}$ и ${ displaystyle gamma _ {n}}$ за счет оптимизации неравенства (1).
При более сильных предположениях о функции ${ displaystyle F}$ Такие как выпуклость, более передовые методы может быть возможно.

Обычно по одному из рецептов выше, конвергенция до местного минимума может быть гарантировано. Когда функция ${ displaystyle F}$ является выпуклый, все локальные минимумы также являются глобальными минимумами, поэтому в этом случае градиентный спуск может сходиться к глобальному решению.

Решение линейной системы

Алгоритм наискорейшего спуска, примененный к Винеровский фильтр.^[7]

Градиентный спуск можно использовать для решения системы линейных уравнений, переформулированной как задача квадратичной минимизации, например, с использованием линейный метод наименьших квадратов. Решение

{ displaystyle A mathbf {x} - mathbf {b} = 0}

в смысле линейных наименьших квадратов определяется как минимизация функции

{ Displaystyle F ( mathbf {x}) = left | A mathbf {x} - mathbf {b} right | ^ {2}.}

Традиционным методом наименьших квадратов для реальных ${ displaystyle A}$ и ${ displaystyle mathbf {b}}$ то Евклидова норма используется, и в этом случае

{ displaystyle nabla F ( mathbf {x}) = 2A ^ {T} (A mathbf {x} - mathbf {b}).}

В этом случае линейный поиск минимизация, нахождение локально оптимального размера шага ${ displaystyle gamma}$ на каждой итерации может выполняться аналитически, а явные формулы для локально оптимальных ${ displaystyle gamma}$ известны.^[8]

Алгоритм редко используется для решения линейных уравнений, при этом метод сопряженных градиентов это одна из самых популярных альтернатив. Количество итераций градиентного спуска обычно пропорционально спектральной номер условия ${ Displaystyle каппа (А)}$ матрицы системы ${ displaystyle A}$ (отношение максимального к минимальному собственные значения из ${ displaystyle A ^ {T} A}$ ), а сходимость метод сопряженных градиентов обычно определяется квадратным корнем из числа обусловленности, т.е. выполняется намного быстрее. Оба метода могут извлечь выгоду из предварительная подготовка, где градиентный спуск может потребовать меньше допущений о предварительном кондиционере.^[9]

Решение нелинейной системы

Градиентный спуск также можно использовать для решения системы нелинейные уравнения. Ниже приведен пример, показывающий, как использовать градиентный спуск для решения трех неизвестных переменных: Икс₁, Икс₂, и Икс₃. В этом примере показана одна итерация градиентного спуска.

Рассмотрим нелинейную систему уравнений

{ displaystyle { begin {cases} 3x_ {1} - cos (x_ {2} x_ {3}) - { tfrac {3} {2}} = 0 4x_ {1} ^ {2} - 625x_ {2} ^ {2} + 2x_ {2} -1 = 0 exp (-x_ {1} x_ {2}) + 20x_ {3} + { tfrac {10 pi -3} {3 }} = 0 end {case}}}

Введем ассоциированную функцию

{ Displaystyle G ( mathbf {x}) = { begin {bmatrix} 3x_ {1} - cos (x_ {2} x_ {3}) - { tfrac {3} {2}} 4x_ { 1} ^ {2} -625x_ {2} ^ {2} + 2x_ {2} -1 exp (-x_ {1} x_ {2}) + 20x_ {3} + { tfrac {10 pi -3} {3}} конец {bmatrix}},}

куда

{ displaystyle mathbf {x} = { begin {bmatrix} x_ {1} x_ {2} x_ {3} end {bmatrix}}.}

Теперь можно определить целевую функцию

{ Displaystyle F ( mathbf {x}) = { frac {1} {2}} G ^ { mathrm {T}} ( mathbf {x}) G ( mathbf {x}) = { frac {1} {2}} left [ left (3x_ {1} - cos (x_ {2} x_ {3}) - { frac {3} {2}} right) ^ {2} + слева (4x_ {1} ^ {2} -625x_ {2} ^ {2} + 2x_ {2} -1 right) ^ {2} + left ( exp (-x_ {1} x_ {2}) + 20x_ {3} + { frac {10 pi -3} {3}} right) ^ {2} right],}

которые мы постараемся минимизировать. В качестве первоначальной догадки воспользуемся

{ displaystyle mathbf {x} ^ {(0)} = mathbf {0} = { begin {bmatrix} 0 0 0 end {bmatrix}}.}

Мы знаем это

{ Displaystyle mathbf {x} ^ {(1)} = mathbf {0} - gamma _ {0} nabla F ( mathbf {0}) = mathbf {0} - gamma _ {0} J_ {G} ( mathbf {0}) ^ { mathrm {T}} G ​​( mathbf {0}),}

где Матрица якобиана ${ displaystyle J_ {G}}$ дан кем-то

{ Displaystyle J_ {G} ( mathbf {x}) = { begin {bmatrix} 3 & sin (x_ {2} x_ {3}) x_ {3} & sin (x_ {2} x_ {3} ) x_ {2} 8x_ {1} & - 1250x_ {2} + 2 & 0 - x_ {2} exp {(-x_ {1} x_ {2})} & - x_ {1} exp ( -x_ {1} x_ {2}) & 20 end {bmatrix}}.}

Рассчитываем:

{ Displaystyle J_ {G} ( mathbf {0}) = { begin {bmatrix} 3 & 0 & 0 0 & 2 & 0 0 & 0 & 20 end {bmatrix}}, qquad G ( mathbf {0}) = { begin { bmatrix} -2,5 - 1 10,472 end {bmatrix}}.}

Таким образом

{ displaystyle mathbf {x} ^ {(1)} = mathbf {0} - gamma _ {0} { begin {bmatrix} -7.5 - 2 209.44 end {bmatrix}},}

и

{ Displaystyle F ( mathbf {0}) = 0,5 left ((- 2,5) ^ {2} + (- 1) ^ {2} + (10,472) ^ {2} right) = 58,456.}

Анимация, показывающая первые 83 итерации градиентного спуска, примененные к этому примеру. Поверхности изоповерхности из

{ Displaystyle F ( mathbf {x} ^ {(n)})}

при текущем предположении

{ Displaystyle mathbf {х} ^ {(п)}}

, а стрелки показывают направление спуска. Из-за небольшого и постоянного размера шага сходимость происходит медленно.

Теперь подходящий ${ displaystyle gamma _ {0}}$ должен быть найден такой, что

{ Displaystyle F влево ( mathbf {x} ^ {(1)} right) Leq F left ( mathbf {x} ^ {(0)} right) = F ( mathbf {0}) .}

Это можно сделать с помощью любого из множества линейный поиск алгоритмы. Можно также просто догадаться ${ displaystyle gamma _ {0} = 0,001,}$ который дает

{ displaystyle mathbf {x} ^ {(1)} = { begin {bmatrix} 0,0075 0,002 - 0,20944 end {bmatrix}}.}

Оценка целевой функции при этом значении дает

{ Displaystyle F влево ( mathbf {х} ^ {(1)} вправо) = 0,5 влево ((- 2,48) ^ {2} + (- 1,00) ^ {2} + (6,28) ^ {2 } right) = 23,306.}

Уменьшение от ${ Displaystyle F ( mathbf {0}) = 58,456}$ к значению следующего шага

{ Displaystyle F влево ( mathbf {х} ^ {(1)} вправо) = 23,306}

- значительное уменьшение целевой функции. Дальнейшие шаги еще больше уменьшат его значение, пока не будет найдено приблизительное решение системы.

Градиентный спуск работает в пространствах любого числа измерений, даже в бесконечномерных. В последнем случае пространство поиска обычно функциональное пространство, и один вычисляет Производная Фреше минимизируемого функционала для определения направления спуска.^[10]

Этот градиентный спуск работает в любом количестве измерений (по крайней мере, в конечном числе), и его можно рассматривать как следствие Неравенство Коши-Шварца. Эта статья доказывает, что величина внутреннего (точечного) произведения двух векторов любой размерности максимальна, когда они коллинеарны. В случае градиентного спуска это будет, когда вектор корректировок независимых переменных пропорционален вектору градиента частных производных.

Градиентный спуск может занять много итераций для вычисления локального минимума с требуемым точность, если кривизна в разные стороны очень отличается для данной функции. Для таких функций предварительная подготовка, который изменяет геометрию пространства, чтобы сформировать наборы уровней функций, например концентрические круги, устраняет медленную сходимость. Однако создание и применение предварительной обработки может быть дорогостоящим в вычислительном отношении.

Градиентный спуск можно комбинировать с линейный поиск, находя локально оптимальный размер шага ${ displaystyle gamma}$ на каждой итерации. Поиск строки может занять много времени. И наоборот, используя фиксированный малый ${ displaystyle gamma}$ может привести к плохой сходимости.

Методы, основанные на Метод Ньютона и инверсия Гессен с помощью сопряженный градиент методы могут быть лучшими альтернативами.^[11]^[12] Как правило, такие методы сходятся за меньшее количество итераций, но стоимость каждой итерации выше. Примером может служить Метод BFGS который заключается в вычислении на каждом шаге матрицы, на которую вектор градиента умножается, чтобы перейти в «лучшее» направление, в сочетании с более сложным линейный поиск алгоритм, чтобы найти "лучшее" значение ${ displaystyle gamma.}$ Для очень больших проблем, где преобладают проблемы с памятью компьютера, метод с ограничением памяти, такой как L-BFGS следует использовать вместо BFGS или самый крутой спуск.

Градиентный спуск можно рассматривать как применение Метод Эйлера для решения обыкновенные дифференциальные уравнения ${ Displaystyle х '(т) = - набла ф (х (т))}$ к градиентный поток. В свою очередь, это уравнение может быть получено как оптимальный регулятор.^[13] для системы управления ${ Displaystyle х '(т) = и (т)}$ с ${ Displaystyle и (т)}$ предоставлено в форме обратной связи ${ Displaystyle и (т) = - набла ф (х (т))}$ .

Расширения

Градиентный спуск можно расширить до ручки ограничения включив проекция на множество ограничений. Этот метод применим только в том случае, если проекцию можно эффективно вычислить на компьютере. При подходящих предположениях этот метод сходится. Этот метод является частным случаем алгоритм вперед-назад для монотонных включений (в том числе выпуклое программирование и вариационные неравенства ).^[14]

Методы быстрого градиента

Еще одно расширение градиентного спуска связано с Юрий Нестеров с 1983 г.,^[15] и впоследствии было обобщено. Он предлагает простую модификацию алгоритма, которая обеспечивает более быструю сходимость для выпуклых задач. Для неограниченных гладких задач метод называется Метод быстрого градиента (КОЖПО) или Метод ускоренного градиента (ГОСА). В частности, если дифференцируемая функция ${ displaystyle F}$ выпуклый и ${ displaystyle nabla F}$ является Липшиц, и не предполагается, что ${ displaystyle F}$ является сильно выпуклый, то ошибка в целевом значении, генерируемая на каждом шаге ${ displaystyle k}$ методом градиентного спуска будет ограничен ${ textstyle { mathcal {O}} left ({ tfrac {1} {k}} right)}$ . При использовании метода ускорения Нестерова ошибка уменьшается при ${ textstyle { mathcal {O}} left ({ tfrac {1} {k ^ {2}}} right)}$ .^[16] Известно, что ставка ${ displaystyle { mathcal {O}} left ({k ^ {- 2}} right)}$ для уменьшения функция стоимости оптимален для методов оптимизации первого порядка. Тем не менее, есть возможность улучшить алгоритм за счет уменьшения постоянного множителя. В оптимизированный градиентный метод (OGM)^[17] уменьшает эту константу в два раза и является оптимальным методом первого порядка для крупномасштабных задач.^[18]

Для задач с ограничениями или негладких FGM Нестерова называют метод быстрого проксимального градиента (FPGM), ускорение метод проксимального градиента.

Импульс

Еще одно расширение, которое снижает риск застревания в локальном минимуме, а также значительно ускоряет сходимость в тех случаях, когда в противном случае процесс мог бы сильно двигаться зигзагом, является импульсный метод, в котором используется импульсный член по аналогии с «массой ньютоновских частиц, движущихся через вязкую среду в консервативном силовом поле».^[19] Этот метод часто используется как расширение обратное распространение алгоритмы, используемые для обучения искусственные нейронные сети.^[20]^[21]

Смотрите также

дальнейшее чтение

Бойд, Стивен; Ванденберге, Ливен (2004). «Безусловная минимизация» (PDF). Выпуклая оптимизация. Нью-Йорк: Издательство Кембриджского университета. С. 457–520. ISBN 0-521-83378-7.
Чонг, Эдвин К. П .; Чак, Станислав Х. (2013). «Градиентные методы». Введение в оптимизацию (Четвертое изд.). Хобокен: Вайли. С. 131–160. ISBN 978-1-118-27901-4.
Химмельблау, Дэвид М. (1972). «Процедуры неограниченной минимизации с использованием производных». Прикладное нелинейное программирование. Нью-Йорк: Макгроу-Хилл. С. 63–132. ISBN 0-07-028921-2.

внешняя ссылка

[1] Лемарешаль, К. (2012). «Коши и градиентный метод» (PDF). Док Математика Экстра: 251–254.

[2] Карри, Хаскелл Б. (1944). «Метод наискорейшего спуска для задач нелинейной минимизации». Кварта. Appl. Математика. 2 (3): 258–261. Дои:10.1090 / qam / 10667.

[3] Барзилай, Джонатан; Борвейн, Джонатан М. (1988). «Двухточечные градиентные методы размера шага». Журнал численного анализа IMA. 8 (1): 141–148. Дои:10.1093 / imanum / 8.1.141.

[4] Флетчер, Р. (2005). «О методе Барзилаи – Борвейна». In Qi, L .; Тео, К .; Ян, X. (ред.). Оптимизация и управление с помощью приложений. Прикладная оптимизация. 96. Бостон: Спрингер. С. 235–256. ISBN 0-387-24254-6.

[5] Вулф, Филип (1969-04-01). «Условия сходимости методов восхождения». SIAM Обзор. 11 (2): 226–235. Дои:10.1137/1011036. ISSN 0036-1445.

[6] Бернштейн, Джереми; Вахдат, Араш; Юэ, Исун; Лю, Мин-Ю (12.06.2020). «О расстоянии между двумя нейронными сетями и устойчивости обучения». arXiv:2002.03432 [cs.LG ].

[7] Хайкин, Саймон С. Теория адаптивных фильтров. Pearson Education India, 2008. - стр. 108-142, 217-242

[8] Юань, Я-сян (1999). «Размеры шага для градиентного метода» (PDF). Исследования AMS / IP по высшей математике. 42 (2): 785.

[9] Баумейстер, Хенрикус; Догерти, Эндрю; Князев, Андрей В. (2015). «Несимметричное предварительное кондиционирование для методов сопряженного градиента и наискорейшего спуска». Процедуры информатики. 51: 276–285. Дои:10.1016 / j.procs.2015.05.241.

[10] Акилов, Г.П .; Канторович, Л.В. (1982). Функциональный анализ (2-е изд.). Pergamon Press. ISBN 0-08-023036-9.

[11] Press, W. H .; Теукольский, С. А .; Vetterling, W. T .; Фланнери, Б. П. (1992). Числовые рецепты на языке C: искусство научных вычислений (2-е изд.). Нью-Йорк: Издательство Кембриджского университета. ISBN 0-521-43108-5.

[12] Струтц, Т. (2016). Подгонка данных и неопределенность: практическое введение в взвешенный метод наименьших квадратов и не только (2-е изд.). Springer Vieweg. ISBN 978-3-658-11455-8.

[13] Росс, И. М. (2019-07-01). «Теория оптимального управления для нелинейной оптимизации». Журнал вычислительной и прикладной математики. 354: 39–51. Дои:10.1016 / j.cam.2018.12.044. ISSN 0377-0427.

[14] Combettes, P. L .; Песке, Ж.-К. (2011). «Методы проксимального расщепления в обработке сигналов». In Bauschke, H.H .; Бурачик, Р.С.; Combettes, P. L .; Elser, V .; Люк, Д. Р .; Волкович, Х. (ред.). Алгоритмы с фиксированной точкой для обратных задач в науке и технике. Нью-Йорк: Спрингер. С. 185–212. arXiv:0912.3522. ISBN 978-1-4419-9568-1.

[15] Нестеров, Ю. (2004). Вводные лекции по выпуклой оптимизации: базовый курс. Springer. ISBN 1-4020-7553-7.

[16] Ванденберге, Ливен (2019). «Быстрые градиентные методы» (PDF). Конспект лекций по EE236C в Калифорнийском университете в Лос-Анджелесе.

[17] Kim, D .; Фесслер, Дж. А. (2016). «Оптимизированные методы первого порядка для гладкой выпуклой минимизации». Математика. Прог. 151 (1–2): 81–107. arXiv:1406.5468. Дои:10.1007 / s10107-015-0949-3. ЧВК 5067109. PMID 27765996. S2CID 207055414.

[18] Дрори, Йоэль (2017). "Точная информационная сложность гладкой выпуклой минимизации". Журнал сложности. 39: 1–16. arXiv:1606.01424. Дои:10.1016 / j.jco.2016.11.001. S2CID 205861966.

[19] Цянь, Нин (январь 1999 г.). «О термине импульса в алгоритмах обучения градиентного спуска» (PDF). Нейронные сети. 12 (1): 145–151. CiteSeerX 10.1.1.57.5612. Дои:10.1016 / S0893-6080 (98) 00116-6. PMID 12662723. Архивировано из оригинал (PDF) 8 мая 2014 г.. Получено 17 октября 2014.

[20] «Адаптация темпа и скорости обучения». Университет Уилламетта. Получено 17 октября 2014.

[21] Джеффри Хинтон; Нитиш Шривастава; Кевин Сверски. «Импульсный метод». Coursera. Получено 2 октября 2018. Часть цикла лекций для Coursera онлайн-курс Нейронные сети для машинного обучения В архиве 2016-12-31 в Wayback Machine.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]