Большой диромбикосододекаэдр - Great dirhombicosidodecahedron
| Большой диромбикосододекаэдр | |
|---|---|
 | |
| Тип | Равномерный звездный многогранник |
| Элементы | F = 124, E = 240 V = 60 (χ = −56) |
| Лица по сторонам | 40{3}+60{4}+24{5/2} |
| Символ Wythoff | | 3/2 5/3 3 5/2 |
| Группа симметрии | ячас, [5,3], *532 |
| Указатель ссылок | U75, C92, W119 |
| Двойной многогранник | Большой дирхомбикосидодекакрон |
| Фигура вершины |  4.5/3.4.3.4.5/2.4.3/2 |
| Акроним Bowers | Gidrid |

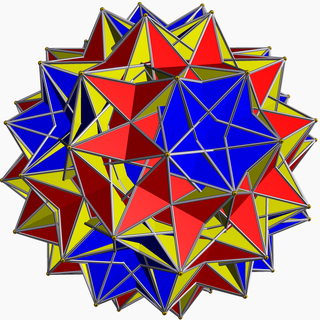
В геометрия, то большой диромбикосододекаэдр (или же большой курносый дисикозидододекаэдр) это невыпуклый однородный многогранник, последняя индексируется как U75. Имеет 124 лица (40 треугольники, 60 квадраты, и 24 пентаграммы ), 240 ребер и 60 вершин.[1]
Это единственный невырожденный однородный многогранник, у которого более шести граней пересекаются в вершине. Каждая вершина состоит из 4 квадратов, которые проходят через центральную ось вершины (и, следовательно, через центр фигуры), чередующиеся с двумя треугольниками и двумя пентаграммами. Еще одна необычная особенность заключается в том, что все грани образуют компланарные пары.
Это также единственный однородный многогранник, который не может быть составлен Строительство Wythoff из сферического треугольника. Он имеет особую Символ Wythoff | 3/2 5/3 3 5/2 относит его к сферическому четырехугольнику. Этот символ предполагает, что это своего рода курносый многогранник, за исключением того, что не курносые грани окружены курносыми треугольниками, как в большинстве курносых многогранников, они окружены курносыми квадратами.
Его прозвали «чудовищем Миллера» (в честь Дж. С. П. Миллер, кто с Х. С. М. Коксетер и М. С. Лонге-Хиггинс перечислил равномерные многогранники в 1954 г.).
Связанные многогранники
Если определение однородного многогранника ослабить, чтобы разрешить любое четное число граней, смежных с ребром, то это определение дает начало еще одному многограннику: большой дизнуб диргомбидодекаэдр который имеет те же вершины и ребра, но с другим расположением треугольных граней.
Вершины и ребра также являются общими с однородными соединениями 20 октаэдров или же 20 тетрагемигексаэдров. 180 из 240 кромок используются совместно с большой курносый додецикосододекаэдр.
 Выпуклый корпус |  Большой курносый додецикосододекаэдр |  Большой диромбикосододекаэдр |
 Большой дизнуб диргомбидодекаэдр |  Соединение двадцати октаэдров |  Соединение двадцати тетрагемигексаэдров |
Декартовы координаты
Декартовы координаты для вершин большого диромбикосододекаэдра все четные перестановки
где τ = (1+√5) / 2 - это Золотое сечение (иногда пишется φ). Эти вершины дают длину ребра 2√2.
Галерея
 Традиционная начинка |  Заполнение по модулю-2 |  Внутренний вид, заполнение по модулю 2 |
Рекомендации
- Коксетер, Гарольд Скотт Макдональд; Longuet-Higgins, M.S .; Миллер, Дж. К. П. (1954), "Равномерные многогранники", Философские труды Лондонского королевского общества. Серия А. Математические и физические науки., 246: 401–450, Дои:10.1098 / рста.1954.0003, ISSN 0080-4614, JSTOR 91532, МИСТЕР 0062446
- Веннингер, Магнус (1974). Модели многогранников. Издательство Кембриджского университета. ISBN 0-521-09859-9. OCLC 1738087.
- Хар'Эль, З. Равномерное решение для равномерных многогранников., Geometriae Dedicata 47, 57-110, 1993. Цви Хар'Эль, Программное обеспечение Kaleido, Изображений, двойные изображения
- Мэдер, Р. Э. Однородные многогранники. Mathematica J. 3, 48-57, 1993.
- Клитцинг, Ричард. "Трехмерные однородные многогранники".
- ^ Медер, Роман. "75: большой диромбикосододекаэдр". MathConsult.


