Интегрирующая сфера - Integrating sphere

Большой интегрирующий шар для измерения на лампочках и маленьких лампах

An интегрирующая сфера (также известный как Сфера Ульбрихта) представляет собой оптический элемент, состоящий из полой сферической полости, внутренняя часть которой покрыта размытый белое светоотражающее покрытие с небольшими отверстиями для входных и выходных портов. Соответствующее свойство - униформа рассеяние или рассеивающий эффект. Лучи света, падающие на любую точку внутренней поверхности, в результате многократного отражения рассеяния равномерно распределяются по всем остальным точкам. Эффекты исходного направления света сведены к минимуму. Интегрирующую сферу можно рассматривать как диффузор который сохраняет власть, но разрушает пространственную информацию. Обычно он используется с некоторым источником света и детектором для измерения оптической мощности. Аналогичным устройством является фокусирующая сфера или сфера Кобленца, которая отличается тем, что имеет зеркальную (зеркальную) внутреннюю поверхность, а не диффузную внутреннюю поверхность.

Даже небольшие коммерческие интегрирующие сферы стоят многие тысячи долларов, в результате чего их использование часто ограничивается промышленностью и крупными академическими учреждениями. Тем не менее, с помощью 3D-печати и самодельных покрытий были созданы экспериментально точные сферы DIY по очень низкой цене.^[1]

Практическая реализация интегрирующей сферы обязана работе Р. Ульбрихта (1849–1923), опубликованной в 1900 году.^[2] Он стал стандартным инструментом в фотометрия и радиометрия. Он имеет преимущество перед гониофотометр для измерения света, испускаемого источником, полная мощность может быть получена за одно измерение.

Теория светособирающего кубического ящика была описана В. Э. Сампнером в 1910 году.^[3]

Теория

Теория интегрирующих сфер основана на следующих предположениях:

Свет, попадающий в стороны сферы, рассеивается рассеянно, т.е. Ламбертовский коэффициент отражения
Только свет, который был рассеян в сфере, попадает в порты или детекторы, используемые для исследования света.

Используя эти предположения, можно рассчитать сферический множитель. Это число представляет собой среднее количество раз, когда фотон рассеивается в сфере, прежде чем он будет поглощен покрытием или улетит через порт. Это число увеличивается с отражательной способностью покрытия сферы и уменьшается с соотношением между общей площадью отверстий и других поглощающих объектов и внутренней площадью сферы. Для получения высокой однородности рекомендуемый множитель сфер составляет 10-25.^[4]Теория далее утверждает, что если вышеупомянутые критерии выполнены, тогда освещенность на любом элементе площади на сфере будет пропорциональна общему лучистому потоку, поступающему в сферу. Абсолютные измерения светового потока экземпляра затем могут быть выполнены путем измерения известного источника света и определения функция передачи или же калибровка изгиб.

Полная выходная освещенность

Для сферы с радиусом r, коэффициентом отражения ρ и потоком источника Φ начальная отраженная освещенность равна:

${displaystyle E = ho {frac {Phi} {4pi r ^ {2}}},}$

Каждый раз при отражении освещенности коэффициент отражения экспоненциально растет. В результате получается уравнение

${displaystyle E = {frac {Phi} {4pi r ^ {2}}}, хо (1 + хо + хо ^ {2} + ...)}$

Поскольку ρ ≤ 1, геометрическая серия сходится, а общая выходная освещенность составляет:^[5]

${displaystyle E = {frac {Phi} {4pi r ^ {2}}}, {frac {ho} {1-ho}},}$

Приложения

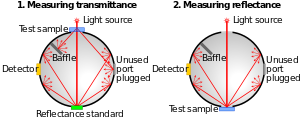
Упрощенный принцип использования интегрирующей сферы для измерения пропускания и отражения тестового образца

Свет, рассеянный внутренней частью интегрирующей сферы, равномерно распределяется по всем углам. Интегрирующая сфера используется в оптических измерениях. Полная мощность (поток) источника света может быть измерена без погрешностей, вызванных характеристиками направленности источника или измерительного устройства. Можно изучать отражение и поглощение образцов. Сфера создает эталонный источник излучения, который можно использовать в качестве фотометрического стандарта.

Сфера коммерческой интеграции. Эта конкретная модель от Электрооптическая промышленность использует четыре отдельные лампы, которые можно указать для достижения требуемой спектральной мощности от ультрафиолетовый через инфракрасный.

Интегрирующие сферы используются для различных оптических, фотометрический или же радиометрический измерения. Они используются для измерения общего света, излучаемого лампой во всех направлениях. Интегрирующая сфера может использоваться для измерения коэффициента диффузного отражения поверхностей, обеспечивая среднее значение по всем углам освещения и наблюдения. Интегрирующую сферу можно использовать для создания источника света с кажущейся интенсивностью, однородной по всем позициям в пределах его круглой апертуры и независимо от направления, за исключением функции косинуса, присущей идеально рассеянным излучающим поверхностям (Ламбертовские поверхности ).

Поскольку весь свет, падающий на входной порт, собирается, детектор, подключенный к интегрирующей сфере, может точно измерить сумму всего окружающего света, падающего на маленькую круглую апертуру. Полная мощность лазерного луча может быть измерена независимо от формы луча, направления падения и положения падения, а также поляризация.

Материалы

Оптические свойства футеровки сферы сильно влияют на ее точность. Необходимо использовать разные покрытия в видимом, инфракрасном и ультрафиолетовом диапазонах волн. Источники освещения высокой мощности могут нагреть или повредить покрытие, поэтому интегрирующая сфера будет рассчитана на максимальный уровень падающей мощности. Используются различные материалы покрытия. Для света видимого спектра ранние экспериментаторы использовали слой оксид магния, и сульфат бария также имеет очень плоскую отражательную способность в видимом спектре. Различные проприетарные PTFE соединения также используются для измерений в видимом свете. Для инфракрасных измерений используется тонко нанесенное золото.

Важное требование к материалу покрытия - отсутствие флуоресценции. Флуоресцентные материалы поглощают коротковолновый свет и повторно излучают свет с более длинными волнами. Из-за большого количества рассеяний этот эффект более выражен в интегрирующей сфере, чем для материалов, облучаемых нормально.

Структура

Теория интегрирующей сферы предполагает однородную внутреннюю поверхность с коэффициентом диффузного отражения, приближающимся к 100%. Отверстия для выхода или проникновения света, используемые для детекторов и источников, обычно называются портами. Общая площадь всех портов должна быть небольшой, менее примерно 5% площади поверхности сферы, чтобы теоретические предположения были верными. Поэтому неиспользуемые порты должны иметь подходящие заглушки, при этом внутренняя поверхность заглушки покрыта тем же материалом, что и остальная часть сферы.

Интегрирующие сферы различаются по размеру от нескольких сантиметров до нескольких метров в диаметре. Меньшие сферы обычно используются для рассеивания поступающего излучения, в то время как более крупные сферы используются для измерения интегрирующих свойств, таких как световой поток лампы или светильников, которые затем помещаются внутрь сферы.

Если входящий свет некогерентен (а не лазерный луч), то он обычно заполняет порт источника, и отношение площади порта источника к площади порта детектора имеет значение.

Перегородки обычно вставляются в сферу, чтобы блокировать прямой путь света от порта источника до порта детектора, поскольку этот свет будет иметь неравномерное распределение.

Смотрите также

Скульптура объединяющей сферы. Находится в кампусе Технического университета Дрездена.

Закон косинусов Ламберта